Chapter 11 Fortgeschrittene Themen der linearen Regression

In diesem Kapitel werden wir auf den formalen Konzepten des Kapitels 6 aufbauen, insbesondere auf den Regeln zur Matrizenalgebra. Damit werden wir die Annahmen und Funktionsweise des OLS-Schätzers genauer untersuchen. Der OLS-Schätzer, den wir bereits im vorigen Kapitel kennengelernt haben, ist das am weitesten verbreitete Schätzverfahren für die lineare Regression. In diesem Kapitel werden wir sehen, dass dies an seinen attraktiven Eigenschaften wie Erwartungstreue, Effizienz und Konsistenz liegt.

Wie alle Schätzverfahren baut der OLS-Schätzer jedoch auf bestimmten Annahmen auf und es muss uns immer klar sein, dass der OLS-Schätzer seine attraktiven Eigenschaften nur hat, wenn diese Annahmen erfüllt sind. Für die Praxis sind also die folgenden vier Fragen relevant:

1. Was sind die relevanten Annahmen des OLS-Schätzers?
2. Was passiert mit dem OLS-Schätzer wenn die Annahmen nicht erfüllt sind?
3. Wie können wir überprüfen ob diese Annahmen erfüllt sind?
4. Was sind mögliche Lösungsstrategien wenn die Annahmen unseres Schätzers nicht erfüllt sind?

Diese Fragen zu beantworten ist die zentrale Herausforderung in diesem Kapitel. Die erste Frage haben wir dabei im vorigen Kapitel bereits angefangen, verbal zu diskutieren. Diese Diskussion soll nun weiter formalisiert, vertieft und schließlich erweitert werden.

Der Fokus des Hauptkapitels liegt dabei auf der zugrundeliegenden Intuition. Daher werden wir uns nicht mit den mathematischen Beweisen beschäftigen, sondern das Verhalten des OLS-Schätzers anhand von Simulationen illustrieren. Für alle Interessierten gibt es jedoch am Ende des Kapitels einen Überblick zu allen relevanten Theoremen und ihren mathematischen Beweisen (siehe Anhang zu Theoremen und Beweisen).

Verwendete Pakete

library(here)
library(tidyverse)
library(data.table)
library(latex2exp)
library(icaeDesign)
library(ggpubr)
library(lmtest)
library(sandwich)
library(MASS)

11.1 Annahmen und Eigenschaften des einfachen OLS Modells

In diesem Abschnitt werden wir zunächst unser Wissen über Matrixnotation aus dem Kapitel 6 verwenden um die uns bereits bekannten Annahmen des OLS Modells aus Kapitel 10 in Matrixschreibweise auszudrücken. Das wird sich als enorm hilfreich erweisen da alle modernen Texte und fortgeschrittenen Lehrbücher die Matrixschreibweise verwenden und alle relevanten Beweise und Herleitung sich dieser Notation bedienen.

Danach werden wir uns mit den wichtigen Eigenschaften Erwartungstreue, Effizienz und Konsistenz von Schätzern beschäftigen. Alles drei sind erstrebenswerte Eigenschaften, über die der OLS Schätzer verfügt wenn die Annahmen für das OLS Modell erfüllt sind. Allerdings kann er diese Eigenschaften verlieren wenn einzelne Annahmen verletzt sind. Um die Konsequenzen verletzter Annahmen zu illustrieren verwenden wir häufig die Methode der Monte Carlo Simulation, die wir am Ende dieses Abschnitts einführen werden.

11.1.1 Annahmen im Matrixschreibweise

An dieser Stelle werden wir die uns aus diesem Abschnitt bekannten verbal formulierten Annahmen für die OLS Schätzung in Matrixschreibweise ausdrücken und ihre Reihenfolge an die in der Literatur typische Reihenfolge anpassen.

Zu diesem Zweck betrachten wir das folgende Modell:

\[\boldsymbol{y} = \boldsymbol{x_1}\beta_1 + ... + \boldsymbol{x_k}\beta_k + \boldsymbol{\epsilon}\]

in dem \(\boldsymbol{y}\) der \(1\times n\) Vektor mit den \(n\) Beobachtungen der abhängigen Variable ist. Für jede der \(k\) unabhängigen Variablen haben wir die Beobachtungen in einem \(1\times n\) Vektor \(\boldsymbol{x_i} (i\in k)\) gesammelt.

Diese \(k\) Vektoren werden häufig in der \(n\times k\) Matrix \(\boldsymbol{X}\) zusammengefasst, sodass die folgende kompakte Schreibweise verwendet werden kann:

\[\boldsymbol{y} = \boldsymbol{X\beta} + \boldsymbol{\epsilon}\]

\(\boldsymbol{\beta}\) ist der Vektor der (unbeobachtbaren) Modellparameter \(\beta_0,...,\beta_k\), die wir schätzen wollen, und \(\boldsymbol{\epsilon}\) ist der Vektor der (ebenfalls unbeobachtbaren) Fehlerterme.

Der OLS Schätzer \(\boldsymbol{\hat{\beta}}\) für \(\boldsymbol{\beta}\) ist durch folgende Gleichung definiert (für die Herleitung siehe hier):

\[\boldsymbol{\hat{\beta}} = \left(\boldsymbol{X'X}\right)^{-1}\left(\boldsymbol{X'y}\right)\]

Unter bestimmten Annahmen hat dieser Schätzer die attraktiven Eigenschaften Erwartungstreue und Effizienz unabhängig der Stichprobengröße und in großen Stichproben zudem die Eigenschaft der Konsistenz. Die relevanten Annahmen sind dabei die folgenden:

A1: Der Zusammenhang zwischen abhängigen und unabhängigen Variablen ist linear

Diese Annahme ergibt sich unmittelbar aus der Formulierung: \(\boldsymbol{y} = \boldsymbol{X\beta} + \boldsymbol{\epsilon}\). Ein Beispiel für einen solchen Zusammenhang findet sich an Abbildung 11.1a.

Wenn der Zusammenhang zwischen abhängigen und unabhängigen Variablen nicht linear ist können wir das klassische OLS Modell in der Regel nicht verwenden. Häufig können wir aber die Daten so transformieren, dass wir deren Verhältnis als linearen Zusammenhang darstellen können. So ist z.B. der folgende Zusammenhang nicht linear:

\[\begin{align} \boldsymbol{y} = \boldsymbol{x_1}^{\beta_1} + e^{\epsilon} \end{align}\]

Wir können aber einfach die Variablen logarithmieren und erhalten somit die folgende lineare Gleichung, die wir dann mit OLS schätzen können:

\[\ln(\boldsymbol{y}) = \ln(\boldsymbol{x_1}){\beta_1} + \boldsymbol{\epsilon}\]

Ein Beispiel für einen solchen Zusammenhang findet sich an Abbildung 11.1b und c.

Insgesamt hat das lineare Regressionsmodell kein Problem mit nichtlinearen Transformationen für die abhängigen Variablen wie \(\ln(\boldsymbol{x_i})\). Nur der funktionale Zusammenhang muss linear sein. Auch die folgende Spezifikation ist demenstprechend kompatibel mit A1, da nur die abhängigen Variablen in einer nichtlinearen Transformation vorkommen:⁹¹

\[\boldsymbol{y} = \boldsymbol{x_1}{\beta_1} + \boldsymbol{x_2^2}{\beta_2} + \boldsymbol{\epsilon}\]

Daher sprechen wir häufig davon, dass mit OLS zu schätzende Zusammenhänge linear in den Parametern sein müssen - nicht notwendigerweise linear per se. Ein Beispiel für einen nichtlinearen Zusammenhang, den wir auch nicht durch eine entsprechende Transformation linearisieren könnten wäre dagegen z.B. durch folgende Gleichung gegeben:

\[\boldsymbol{y} = \boldsymbol{x_1}{\beta_1} + \boldsymbol{x_2^{\beta_2}} + \boldsymbol{\epsilon}\] Ein Beispiel für einen solchen Zusammenhang findet sich an Abbildung 11.1. Wir werden uns später im Kapitel mit der Frage beschäftigen welche funktionalen Transformationen besonders hilfreich sind, nichtlineare Zusammenhänge in die lineare Form zu bringen.

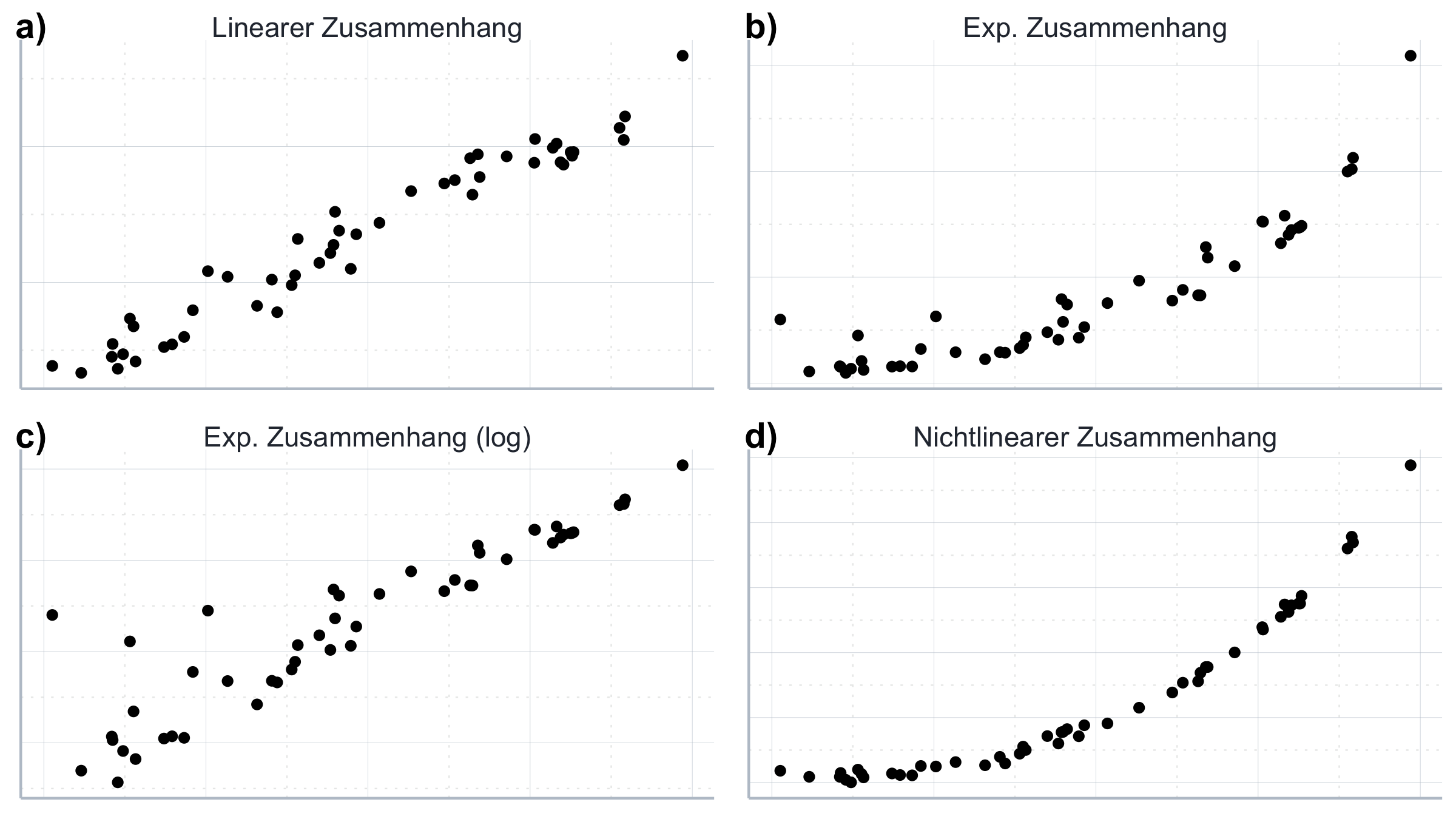
Abbildung 11.1: Lineare und nichtlineare Zusammenhänge.

A2: Exogenität der unabhängigen Variablen

Die Annahme kombiniert die beiden Annahmen, die wir im vorigen Kaptiel unter dem Titel “Unabhängigkeit der Fehler mit den erklärenden Variablen” und “Erwartungswert der Fehler gleich Null” kennen gelernt haben. In der fortgeschrittenen Literatur ist die Referenz zur Exogenität der unabhängigen Variablen gebräuchlicher. Formal können wir schreiben:

\[\mathbb{E}\left[\boldsymbol{\epsilon} | \boldsymbol{x} \right]=0\]

Daher kommt der Begriff “Exogenität”: Die unabhängigen Variablen enthalten keine Informationen über die Fehlerterme. Mit Informationen über \(\boldsymbol{x}\) können wir die Fehler des Modells also nicht vorhersagen - denn \(\boldsymbol{x}\) ist exogen. Man kann übrigens formal zeigen, dass \(\mathbb{E}\left[\boldsymbol{\epsilon} | \boldsymbol{x} \right]=0\) auch impliziert dass \(\mathbb{E}\left[\boldsymbol{\epsilon}\right]=0\).⁹² Der bedingte Erwartungswert von Null impliziert also den unbedingten Erwartungswert von Null - aber nicht umgekehrt.

Manchmal wird daher auch eine noch strengere Annahme verwendet: strikte Exogenität. Darunter verstehen wir die Annahme, dass \(\mathbb{E}\left[\epsilon_i | \boldsymbol{X} \right]=0\) bzw. für alle \(\epsilon_i\): \(\mathbb{E}\left[\boldsymbol{\epsilon} | \boldsymbol{X} \right]=0\). Hier nehmen wir sogar an, dass jeder einzelne Fehlerterm auch mit den unabhängigen Variablen für andere Beobachtungen nicht korreliert. Das impliziert, dass Cov\((\epsilon_i, \boldsymbol{x})=0\forall i\).

Bedingter vs. unbedingter Erwartungswert der Fehler Auf den ersten Blick klingt es komisch, dass der bedingte Erwartungswert der Fehler von Null, \(\mathbb{E}\left[\boldsymbol{\epsilon} | \boldsymbol{x} \right]=0\), den unbedingten Erwartungswert von Null, \(\mathbb{E}\left[\boldsymbol{\epsilon}\right]=0\), impliziert, aber nicht andersherum. Abbildung 11.2 illustriert dieses Problem.

Abbildung 11.2: Exogenität und strikte Exogenität.

In Plot a) in Abbildung 11.2 haben wir einen bedingten Erwartungswert von Null, also \(\mathbb{E}\left[\boldsymbol{\epsilon} | \boldsymbol{x} \right]=0\): für jede beliebige Beobachtung in \(\boldsymbol{x}\) ist der Erwartungswert der Fehler Null. Entsprechend ist der Erwartungswert für alle Fehler zusammen auch Null: \(\mathbb{E}\left[\boldsymbol{\epsilon} \right]=0\). In Plot b) aus Abbildung 11.2 ist der bedingte Erwartungswert nicht Null: \(\mathbb{E}\left[\boldsymbol{\epsilon} | \boldsymbol{x} \right]\neq0\) für die untere Hälte der Beobachtungen in \(\boldsymbol{x}\) ist der Erwartungswert \(1\), für die obere Hälfte der Beobachtungen ist der Erwartungswert \(-1\). Für die gesamten Daten ergibt sich dabei auch ein Erwartungswert von \(0\), also \(\mathbb{E}\left[\boldsymbol{\epsilon} \right]=0\), allerdings eben nicht für jede einzelne Beobachtung. Häufig tritt diese Problem bei quadratischen Zusammenhängen auf.

Wichtig ist festzuhalten, dass dies eine Annahme über nicht zu beobachtende Größen darstellt: die tatsächlichen Fehlerterme \(\boldsymbol{\epsilon}\) können wir in der Praxis nicht beobachten. Wir sprechen daher auch von einer Annahme über die Population. Alles was wir aus der Population direkt beobachten können ist eine Stichprobe. Und innerhalb der Stichprobe können wir als Annäherung der Fehlerterme \(\boldsymbol{\epsilon}\) die Residuen \(\boldsymbol{e}\) berechnen. Die ‘echten’ Fehlerterme können wir aber nicht beobachten.

A3: Keine perfekte Multikollinearität

Die Annahme, dass die unabhängigen Variablen nicht linear voneinander abhängig sind ist notwendig damit der OLS Schätzer \(\boldsymbol{\hat{\beta}} = \left(\boldsymbol{X'X}\right)^{-1}\left(\boldsymbol{X'Y}\right)\) überhaupt berechnet werden kann. Denn wären zwei oder mehrere unabhängige Variablen linear abhängig könnten wir von \(\boldsymbol{X}\) keine Inverse \(\boldsymbol{X}^{-1}\) bilden und der OLS Schätzer von \(\boldsymbol{\beta}\) wäre nicht identifizierbar. Häufig wir diese Annahme auch in ‘Matrizensprache’ formuliert. Dann sprechen wir von der Annahme, dass die Matrix \(\boldsymbol{X}\) vollen Rang hat. Damit ist aber das gleiche gemeint. Die Annahme impliziert zudem, dass \(n\geq k\) und dass es eine gewisse Variation in den unabhängigen Variablen gibt. All das ist in der Praxis aber immer erfüllt - nur mit dem Problem der nicht perfekten Multikollinearität - also der Situation wo die abhängigen Variablen stark miteinander korrelieren - müssen wir uns häufig herumschlagen. Doch dazu später mehr.

A4: Konstante Varianz und keine Autokorrelation der Fehlerterme

Vorher hatten wir diese beiden Annahmen als separate Annahmen formuliert. In der Literatur werden sie jedoch oft zusammengefasst, weil sich beide Annahmen um die Struktur der Varianz-Kovarianz-Matrix einer Schätzung drehen. Für eine Schätzung mit \(n\) Beobachtungen handelt es sich dabei um eine \(n\times n\)-Matrix, auf deren Hauptdiagonalen die Varianzen der Fehlerterme und in den sonstigen Elementen die Kovarianzen der einzelnen Fehlerpaare gesammelt sind. Für den Fall von zwei unabhängigen Variablen hätten wir also folgende Varianz-Kovarianz Matrix:

\[ \left( \begin{array}{rr} Var(\epsilon_1 | \boldsymbol{X}) & Cov(\epsilon_1, \epsilon_2 | \boldsymbol{X}) \\ Cov(\epsilon_2, \epsilon_1 | \boldsymbol{X}) & Var(\epsilon_2 | \boldsymbol{X}) \end{array} \right) \]

Die Annahme der konstanten Varianz - oder “Homoskedastizität” - bezieht sich also auf die Hauptdiagonale der Varianz-Kovarianz-Matrix und sagt:

\[Var(\epsilon_i | \boldsymbol{X}) = \sigma^2 \quad \forall i \]

Die Annahme nichtautokorrelierter Fehler bezieht sich dann auf die Elemente außerhalb der Hauptdiagonalen der Varianz-Kovarianz-Matrix und sagt:

\[Cov(\epsilon_i, \epsilon_j | \boldsymbol{X}) = 0 \quad \forall i\neq j \]

Bei den Fehlertermen \(\epsilon_i\) handelt es sich ja im Zufallsvariablen. Aufgrund der Definition der Varianz und A2, gemäß derer gilt, dass \(\mathbb{E}(\epsilon|\boldsymbol{X})=0\), bekommen wir für die Varianz der Fehler:

\[\begin{align} Var(\epsilon_i|\boldsymbol{X})&=\mathbb{E}\left[\left(\epsilon_i-\mathbb{E}(\epsilon_i|\boldsymbol{X})\right)^2|\boldsymbol{X}\right]\nonumber\\ &=\mathbb{E}\left[\epsilon_i^2 -2\epsilon_i\mathbb{E}(\epsilon_i|\boldsymbol{X}) +\mathbb{E}(\epsilon_i|\boldsymbol{X})^2|\boldsymbol{X}\right]\nonumber\\ &=\mathbb{E}\left[\epsilon_i^2|\boldsymbol{X}\right]=\mathbb{E}\left[\epsilon_i\epsilon_i|\boldsymbol{X}\right]\nonumber \end{align}\]

Die zweite Zeile ergibt sich dabei aus der zweiten binomischen Formel. Für die Kovarianz gilt entsprechend:

\[\begin{align} Cov(\epsilon_i, \epsilon_j|\boldsymbol{X}) &= \mathbb{E}\left[ \left(\epsilon_i-\mathbb{E}(\epsilon_i|\boldsymbol{X}) \right)\left(\epsilon_j-\mathbb{E}(\epsilon_j|\boldsymbol{X}) \right) |\boldsymbol{X}\right] \nonumber\\ &= \mathbb{E}\left[ \left( \epsilon_i\epsilon_j - \epsilon_i \mathbb{E}(\epsilon_j|\boldsymbol{X}) - \epsilon_j \mathbb{E}(\epsilon_i|\boldsymbol{X}) + \mathbb{E}(\epsilon_j|\boldsymbol{X}) \mathbb{E}(\epsilon_i|\boldsymbol{X}) \right) |\boldsymbol{X}\right]\nonumber\\ &= \mathbb{E}\left[\epsilon_i\epsilon_j|\boldsymbol{X}\right]\nonumber \end{align}\]

Hier haben wir in der zweiten Zeile die dritte binomische Formel verwendet.

Daher kann die Annahme von Homoskedastizität und keiner Autokorrelation auch folgendermaßen ausgedrückt werden:

\[\mathbb{E}(\boldsymbol{\epsilon\epsilon'| X}) = \left( \begin{array}{rrrr} \mathbb{E}(\epsilon_1\epsilon_1|\boldsymbol{X}) & \mathbb{E}(\epsilon_1\epsilon_2|\boldsymbol{X}) & ... & \mathbb{E}(\epsilon_1\epsilon_n|\boldsymbol{X})\\ \mathbb{E}(\epsilon_2\epsilon_1|\boldsymbol{X}) & \mathbb{E}(\epsilon_2\epsilon_2|\boldsymbol{X}) & ... & \mathbb{E}(\epsilon_2\epsilon_n|\boldsymbol{X})\\ & & \vdots & \\ \mathbb{E}(\epsilon_n\epsilon_1|\boldsymbol{X}) & \mathbb{E}(\epsilon_n\epsilon_2|\boldsymbol{X}) & ... & \mathbb{E}(\epsilon_n\epsilon_n|\boldsymbol{X})\\ \end{array} \right) = \left( \begin{array}{rrrr} \sigma^2 & 0 & ... & 0 \\ 0 & \sigma^2 & ... & 0 \\ & & \vdots & \\ 0 & 0 & ... & \sigma^2 \\ \end{array} \right)\]

oder zusammengefasst:

\[\mathbb{E}(\boldsymbol{\epsilon\epsilon'| X}) = \sigma^2\boldsymbol{I}\]

Alternativ wird die Annahme auch mit Referenz auf die Varianz-Kovarianz-Matrix \(\boldsymbol{\Omega}\) angegeben: \(\boldsymbol{\Omega}=\sigma^2\boldsymbol{I}\).

A5: Normalverteilung der Fehlerterme:

Die letzte typischerweise gemachte Annahme ist die der Normalverteilung der Fehlerterme, bedingt wie immer auf die unabhängigen Variablen:

\[\boldsymbol{\epsilon|\boldsymbol{X}} \propto \mathcal{N}(0, \sigma^2)\]

Diese Annahme ist weniger zentral als die anderen Annahmen, weswegen sie häufig als ‘optional’ bezeichnet wird. Der Grund dafür ist, dass die gleich eingeführten Eigenschaften des OLS-Schätzers der Erwartungstreue, Effizienz und Konsistenz nicht von der Korrektheit von A5 abhängen. Vielmehr erleichtert diese Annahme die Durchführung der Hypothesentests, die dem Konzept der statistischen Signifikanz zugrunde liegen (siehe Abschnitt 10.3.2 in Kapitel 10).

11.1.2 Erwartungstreue, Effizienz und Konsistenz

Unter den oben beschriebenen Annahmen weist der Schätzer \(\boldsymbol{\hat{\beta}}\) drei wichtige Eigenschaften auf: (1) er ist erwartungstreu und (2) er ist effizient, auch in kleinen Stichproben. In großen Stichproben ist er zudem (3) konsistent. Alle Eigenschaften beziehen sich auf die Verteilung von \(\boldsymbol{\hat{\beta}}\) (wie im einführenden Kapitel beschrieben handelt es sich bei \(\boldsymbol{\hat{\beta}}\) ja um eine Zufallsvariable).

Ohne die Konzepte schon formal eingeführt zu haben wollen dennoch bereits an dieser Stelle festhalten, dass für die Erwartungstreue nur A1 und A2 relevant sind. Annahmen A4 und A5 sind nur für Inferenz und Standardfehler sowie die Effizienz von Bedeutung. A3 ist wie oben beschrieben notwendig, damit der OLS Schätzer überhaupt identifizierbar ist.

Unter Erwartungstreue verstehen wir die Eigenschaft, dass der Schätzer im Mittel den ‘wahren Wert’ \(\beta\) trifft, also \(\mathbb{E}(\hat{\boldsymbol{\beta}})=\beta\). Der Schätzvorgang ist also nicht systematisch verzerrt. Das bedeutet natürlich nicht, dass dies für eine einzelne Schätzung gilt \(\hat{\boldsymbol{\beta}}=\beta\), aber dass \(\beta\) der wahrscheinlichste Wert für \(\hat{\boldsymbol{\beta}}\) ist. Oder technisch: das Mittel unendlich vieler Schätzungen mit \(\hat{\boldsymbol{\beta}}\) ist gleich \(\beta\).

Diese Eigenschaft des OLS-Schätzers wird in Abbildung 11.3 illustriert.

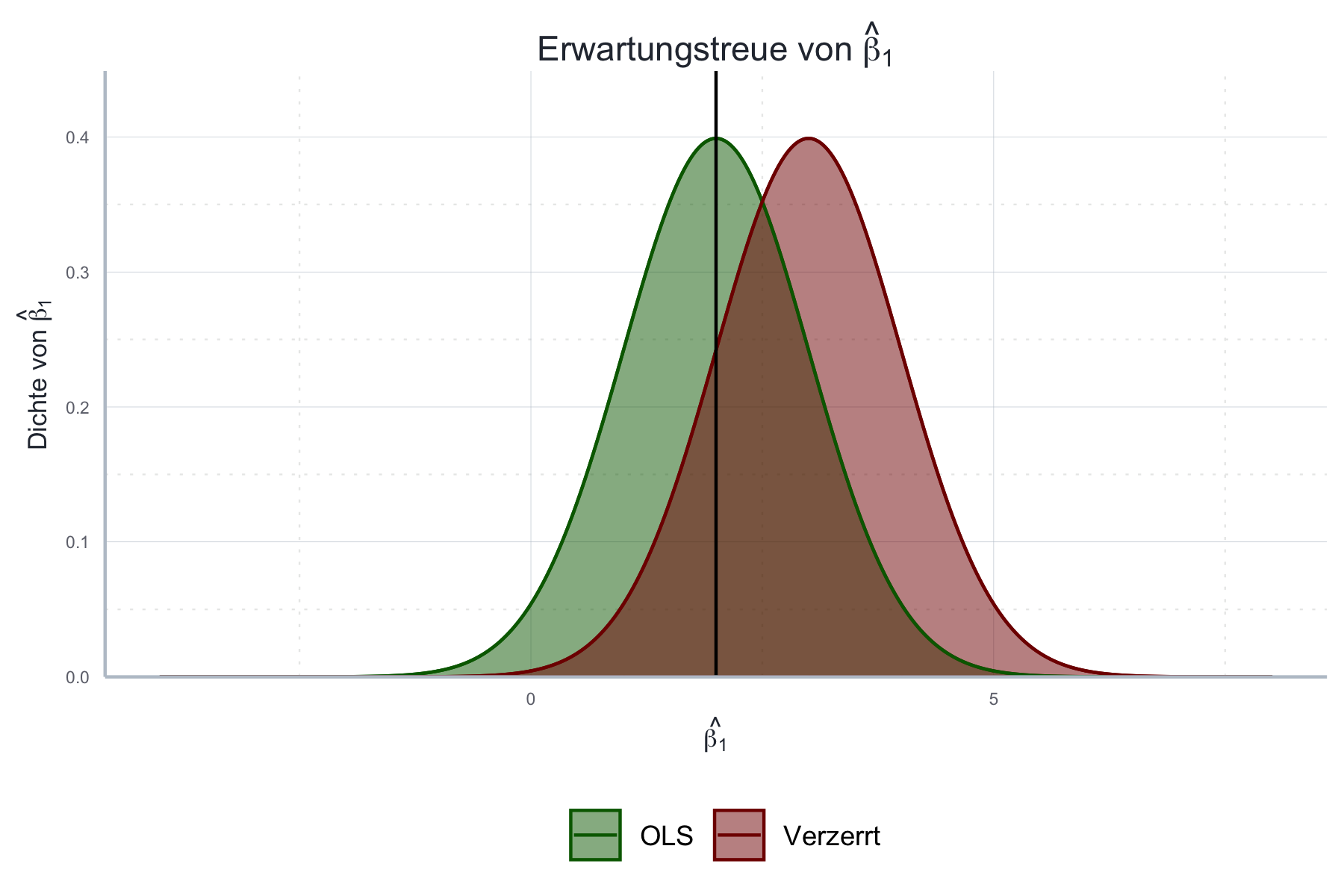
Abbildung 11.3: Erwartungstreue von \(\hat{\boldsymbol{\beta}}\) unter Annahmen 1 bis 3.

Wir können beweisen, dass \(\hat{\boldsymbol{\beta}}\) unter Annahmen A1, A2 und A3 erwartungstreu ist. Dies gilt unabhängig der Stichprobengröße und unabhängig davon ob Annahmen A4 und A5 erfüllt sind. Der mathematische Beweis findet sich im Anhang 11.10 (siehe Theorem ??).

Wie oben bereits erwähnt resultiert daraus natürlich nicht, dass für jede einzelne Schätzung der Wert des Schätzers \(\hat{\boldsymbol{\beta}}\) gleich dem wahren Wert \(\boldsymbol{\beta}\) ist. Jede Schätzung ist aufgrund der Fehler immer mit Unsicherheit behaftet. Diese Unsicherheit können wir über die Varianz des Schätzers \(\hat{\boldsymbol{\beta}}\) messen: je größer die Varianz desto größer die Unsicherheit für die einzelne Schätzung. Wir können die Varianz einer Schätzung auch ausrechnen und als Standardfehler der Schätzer angeben. R gibt uns diese Werte immer automatisch mit aus. Wie die Schätzer hergeleitet und geschätzt werden können Sie über Theorem ?? und ?? im Anhang 11.10 nachvollziehen.

Besonders relevant ist in diesem Kontext die Eigenschaft der Effizienz. Unter Effizienz verstehen wir die Eigenschaft, dass es keinen alternativen Schätzer für \(\beta\) gibt, der eine geringere Varianz aufweist. Effizienz ist dabei ein relatives Maß: ein Schätzer ist effizienter als ein anderer, wenn seine Varianz geringer ist und für den Schätzer \(\hat{\boldsymbol{\beta}}\) gilt, dass es unter A1-A4 keinen anderen linearen erwartungstreuen Schätzer gibt, der noch effizienter ist als \(\hat{\boldsymbol{\beta}}\).

Die Eigenschaft der Effizienz wird in folgender Abbildung 11.4 illustriert.

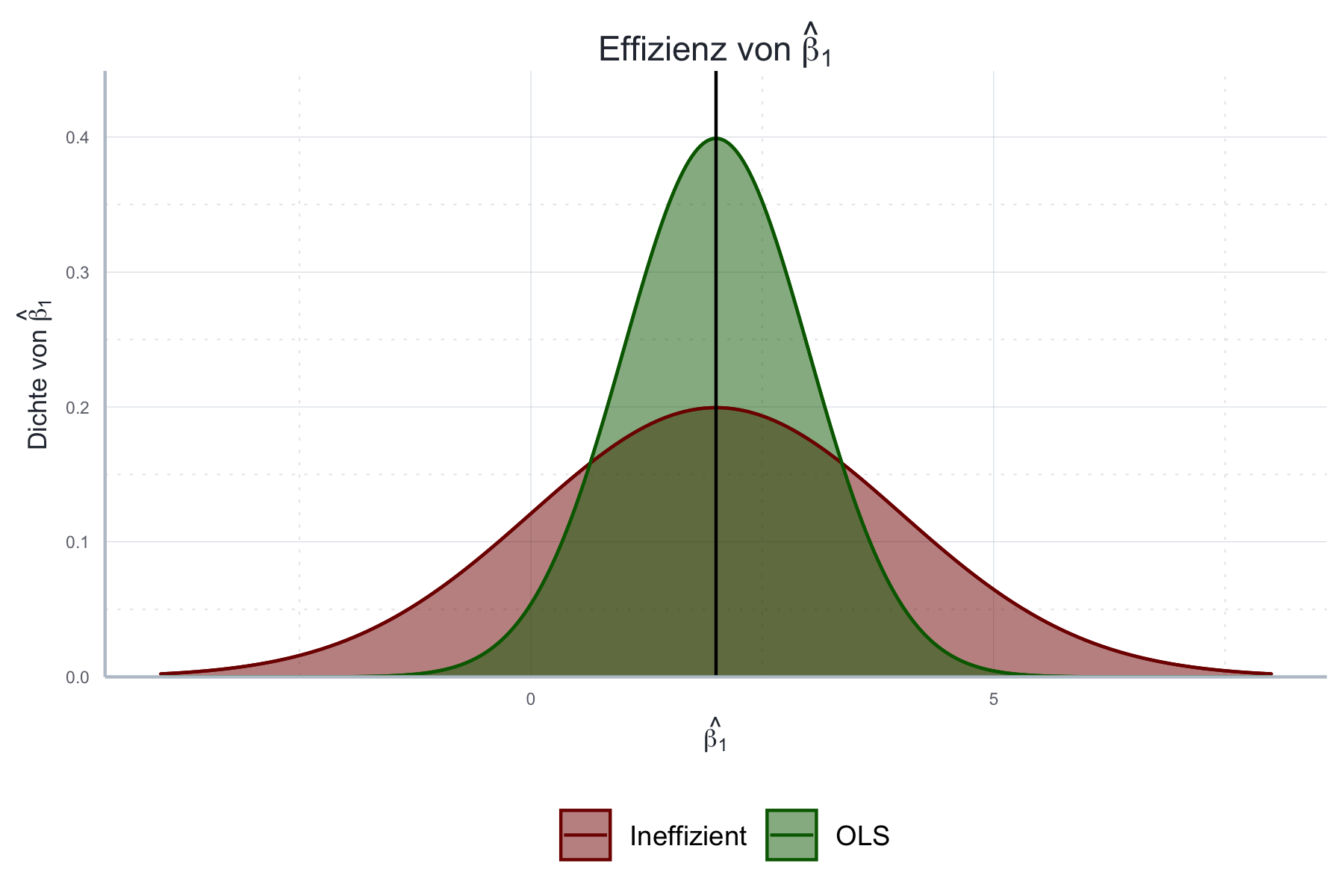
Abbildung 11.4: Effizienz von \(\hat{\boldsymbol{\beta}}\) unter Annahmen 1 bis 4.

Da wir hier die zugrundeliegenden Daten selbst herstellen wissen wir, dass für den wahren Wert gilt \(\beta_1=2.0\). Um die Effizienz des OLS-Schätzers beweisen zu können reichen Annahmen A1-A3 nicht aus: hierfür benötigen wir auch die Annahme A4: Konstante Varianz und keine Autokorrelation der Fehlerterme. Unter Annahmen A1-A4 gilt die Effizienz des OLS-Schätzers auch unabhängig von der Stichprobengröße. Für den Beweis siehe Theorem im Anhang.

Dass die Eigenschaften der Erwartungstreue und Effizienz beim OLS-Schätzer unabhängig von der Stichprobengröße gelten ist eine tolle Sache. Solche stichprobenunabhängigen Beweise funktionieren in realen Settings, in denen bestimmte Annahmen leicht verletzt sind und die zu schätzenden Funktionen komplexer werden, häufig nicht. Daher versucht man Eigenschaften von Schätzern wenigstens für große Stichproben zu beweisen. Diese Beweise sind wegen bestimmten Gesetzen wie dem Gesetz der großen Zahl oder dem Zentralen Grenzwertsatz oft deutlich einfacher. Wie sprechen dann von asymptotischen Eigenschaften, da sie für den Schätzer zutreffen wenn die Stichprobengröße gegen Unendlichkeit wächst.

Allerdings bleibt dann unklar welche Eigenschaften der Schätzer in kleinen Stichproben tatsächlich hat. Auch ab welcher Größe eine Stichprobe als “groß” gilt kann nicht ohne Weiteres beantwortet werden. Um die Schätzereigenschaften für kleine Stichproben zu untersuchen bleibt dann nur die Methode der Monte Carlo Simulation, die weiter unten eingeführt wird.

Vorher wollen wir jedoch die wichtigste Eigenschaft von Schätzern für große Stichproben anhand des OLS-Schätzers einführen: die Konsistenz. Ein konsistenter Schätzer trifft im Mittel den wahren Wert und seine Varianz geht mit wachsender Stichprobengröße gegen Null. Wir können also sagen, dass unsere Schätzungen bei wachsender Stichprobengröße immer genauer wird.

Der Unterschied zwischen Erwartungstreue und Konsistenz Auf den ersten Blick erscheinen die beiden Konzepte eng verwandt, weil beide eine Aussage über den Erwartungswert des OLS-Schätzers treffen. Allerdings gilt die Erwartungstreue unabhängig von der Stichprobengröße: auch in kleinen Stichproben gilt, dass \(\mathbb{E}(\hat{\boldsymbol{\beta}})=\beta\). Die Konsistenz dagegen bezieht sich auf das Verhalten des OLS-Schätzers wenn die Stichprobe immer größer wird. Darüber hinaus macht die Konsistenz auch eine Aussage über die Größe der Varianz des Schätzers: diese geht bei immer größeren Stichproben gegen Null. Das heißt bei sehr großen Stichproben können wir auch bei einer einzelnen Schätzung davon ausgehen, dass wir den wahren Wert ziemlich genau treffen. Eine solche Aussage können wir aus der Erwartungstreue nicht ableiten: dass wir im Mittel den wahren Wert treffen macht überhaupt keine Aussage über die einzelne Schätzung. Auch die Eigenschaft der Effizienz ist hier nur bedingt hilfreich, weil sie nur besagt, dass der OLS-Schätzer der Schätzer mit der geringsten Varianz ist - aber nicht wie gering diese Varianz ist. Manchmal ist auch die geringste Varianz sehr groß.

Formal drücken wir dies unter Verwendung von Grenzwerten aus:

\[\lim_{N\rightarrow\infty}\mathbb{P}(|\hat{\beta}-\beta|>\epsilon)=0\]

wobei \(\epsilon\) hier eine beliebig kleine Zahl ist.

Wenn wir asymptotische Eigenschaften ausdrücken wollen verwenden wir häufig den Operator \(\plim\). Das steht für probability limit und drückt die Idee der letzten Formel aus: das probability limit einer ZV ist der Wert auf den diese ZV bei unendlich vielen Ziehungen konvergieren wird. Wir sagen dann auch: die ZV konvergiert stochastisch gegen einen Wert.⁹³ Oder formal:

\[\lim_{N\rightarrow\infty}\mathbb{P}(|X_N-X|>\epsilon)=0\]

Wir können die Idee der letzten Gleichung also auch folgendermaßen ausdrücken:

\[\plim (\hat{\beta})=\beta\]

In der klassischen statistischen Analyse betrachten wir Erwartungstreue als eine notwendige Eigenschaft: wir möchten in der Regel keine Schätzer verwenden, deren geschätzte Werte systematisch von dem wahren Wert abweichen. Es sei an dieser Stelle jedoch bereits erwähnt, dass es sinnvolle Ausnahmen von dieser Regel geben kann, nämlich dann wenn wir große Zugewinne an Effizienz für kleine Abstriche in der Erwartungstreue ‘erkaufen’ können.

In der Literatur wird diese Fragestellung unter dem Stichwort bias-variance trade-off diskutiert und ist vor allem dann relevant, wenn Sie mit Ihrem Regressionsmodell Vorhersagen treffen wollen. Weitergehende Informationen dazu finden Sie in der weiterführenden Literatur. An dieser Stelle wollen wir uns aber zunächst auf die erwartungstreuen (und konsistenten) Schätzer konzentrieren, da dies tatsächlich auch die am weitesten verbreiteten Schätzmethoden sind.

11.1.3 Abweichungen von den OLS Annahmen

Wenn alle Annahmen des OLS-Schätzers erfüllt sind können wir also ohne Bedenken die Parameter unseres statistischen Modells mit der klassischen OLS Methode schätzen. Aber was ist wenn eine Annahme nicht erfüllt ist?

Im Folgenden wollen wir uns diesem Problem annähern indem wir die folgenden Fragen für die verschiedenen Annahmen anhand der folgenden vier Leitfragen diskutieren: (1) Unter welchen praktisch relevanten Situationen kann die Annahme verletzt sein? (2) Wie können wir testen ob die Annahme verletzt ist? (3) Was sind die Konsequenzen wenn die Annahme verletzt ist? (4) Was können wir tun um trotz verletzter Annahme konsistente und möglichst effiziente Schätzer zu bekommen?

Diese Fragen sind in der der Praxis nicht einfach zu beantworten. Ein Grund dafür ist, dass wir die ‘wahren Werte’ der zu schätzenden Parameter in der Regel nicht beobachten können. Da wir zudem den ‘wahren’ datenerzeugenden Prozess nicht kennen, können wir nie mit Sicherheit sagen, ob eine bestimmte Annahme verletzt ist oder nicht.

Dennoch gibt es zwei Möglichkeiten die relevanten Informationen zu den Schätzern zu bekommen: zum einen können wir häufig mathematisch beweisen, dass ein Schätzer erwartungstreu oder effizient ist. Ein Beispiel dafür ist der Beweis der Erwartungstreue des OLS-Schätzers hier oder der Beweis der Effizienz des OLS-Schätzers hier. Dies ist aber nicht immer möglich und manchmal auch recht aufwendig und wenig intuitiv.

Die zweite Möglichkeit ist die Analyse von Schätzern mit Hilfe von künstlichen Datensätzen und so genannten Monte Carlo Simulationen (MCS). Bei einer MCS definieren wir unseren datenerzeugenden Prozess selbst und erstellen dann einen künstlichen Datensatz, an dem wir dann die Eigenschaften von Schätzern untersuchen können. Diese Vorgehensweise ist zwar weniger ‘sicher’ als ein mathematischer Beweis aber häufig intuitiver und in vielen Fällen tatsächlich auch die einzige Möglichkeit, inbesondere wenn wir Schätzereigenschaften für kleine Stichproben analysieren wollen. Daher wird diese Methode im Folgenden kurz beschrieben und später für die Illustration der Folgen von verletzten Annahmen verwendet.

11.1.4 Monte Carlo Simulationen in R

Der Ablauf einer Monte Carlo Simulation ist immer der Folgende:

1. Definiere das zu untersuchende Merkmal des datenerzeugenden Prozesses
2. Formalisiere den datenerzeugenden Prozess als Funktion
3. Erstelle viele künstliche Stichproben für das zu untersuchende Merkmal; erstelle dabei eine Kontrollgruppe in der das zu untersuchende Merkmal nicht vorhanden ist und eine Testgruppe mit dem Merkmal und wende den zu untersuchenden Schätzer auf die künstlichen Stichproben an
4. Analysiere die Verteilung des Schätzers für die Kontrollgruppe und die Testgruppe
5. Interpretiere die Ergebnisse

Wir erstellen also selbst einen datenerzeugenden Prozess und untersuchen dann das Verhalten des uns interessierenden Schätzers im Kontext dieses datenerzeugenden Prozesses. Wenn wir z.B. untersuchen möchten welchen Effekt Heteroskedastie auf den OLS Schätzer hat dann erstellen wir künstliche Datensätze über einen datenerzeugenden Prozess in den wir Heteroskedastie eingebaut haben und und über einen Prozess für den wir wissen, dass er durch Homoskedastie gekennzeichnet ist. Dann schätzen wir ein Modell jeweils für die beiden Prozesse und vergleichen die Eigenschaften des OLS-Schätzers. Somit können wir Rückschlüsse auf die Implikationen von Heteroskedastie schließen.

Im Folgenden wollen wir die Methode der Monte Carlo Simulation über genau dieses Beispiel einführen.

1. Schritt: Definition des zu untersuchenden Merkmals

Wie gerade beschrieben möchten wir untersuchen welchen Effekt Heteroskedastie auf die Eigenschaften des OLS Schätzers hat. Das zu untersuchende Merkmal des datenerzeugenden Prozesses ist also Heteroskedastie.

2. Schritt: Formalisierung des datenerzeugenden Prozesses

Wir formalisieren jetzt einen datenerzeugenden Prozess, der alle Annahmen des OLS Schätzers erfüllt außer ggf. der Annahme der Homoskedastie. Der Einfachheit halber wollen wir einen Prozess mit einer erklärenden Variable erstellen, also einen Prozess, der durch folgende Gleichung beschrieben werden kann:

\[Y = \beta_0 + \beta_1 x_1 + \epsilon\]

wobei wir annehmen, dass \(\epsilon \propto \mathcal{N}(\mu, \sigma^2)\) und \(\sigma^2\) im Falle der Kontrollgruppe konstant (Fall der Homoskedastie) und im Falle der Testgruppe variabel ist (Fall der Heteroskedastie).

Wir definieren also folgende Funktion, die für gegebene Werte für \(\beta_0\) und \(\beta_1\) und ein gegebenes \(\boldsymbol{X}\) eine Stichprobe erstellt indem \(\boldsymbol{y}\) gemäß des Modells \(y=\beta_0 + \beta_1 x + \epsilon\) künstlich hergestellt wird.

dgp <- function(x1, beta0, beta1, hetero=FALSE){
  y <- rep(NA, length(x1))
  sd_hetero <- 0.25 * x1
  sd_homo <- mean(sd_hetero)
  if (hetero){
    errors <- rnorm(n = length(x1), mean = 0, 
                    sd = sd_hetero)
  } else {
    errors <- rnorm(n = length(x1), mean = 0, 
                    sd = sd_homo
                    )
  }
  for (i in 1:length(x1)){
    y[i] <- beta0 + beta1*x1[i] + errors[i]
  }
  final_data <- dplyr::tibble(y=y, x1=x1, errors=errors)
  return(final_data)
}

3. Schritt: Künstlichen Datensatz erstellen und Schätzer darauf anwenden

Wir simulieren nun das Ziehen einer Stichprobe aus dem künstlich erstellten datengenerierenden Prozess (DGP) indem wir jeweils 1000 Beobachtungen kreieren. Da das Ziehen einer Stichprobe immer ein Zufallsprozess ist erstellen wir 1000 Stichproben und wenden darauf dann jeweils unseren OLS-Schätzer an. Die geschätzten Koeffizienten und Standardfehler speichern wir in einer Liste, da wir sie später dann analysieren wollen.

Dazu definieren wir die folgende Funktion:

mcs <- function(n_stichproben, 
                x1, wahres_b0, wahres_b1, schaetzgleichung,
                heterosk=FALSE){
  schaetzung_b1 <- rep(NA, n_stichproben)
  stdfehler_b1 <- rep(NA, n_stichproben)
  for (i in 1:n_stichproben){
    # Stichprobe ziehen:
    stichprobe <- dgp(x1 = x1, beta0 = wahres_b0, 
                      beta1 = wahres_b1, 
                      hetero = heterosk)
    # Parameter schätzen:
    schaetzung <- summary(
      lm(formula = schaetzgleichung, 
         data = stichprobe)
      )
    # Relevante Werte speichern:
    schaetzung_b1[i] <- schaetzung$coefficients[2]
    stdfehler_b1[i] <- schaetzung$coefficients[4]
  }
  # In einer Tabelle zusammenfassen:
  Fall_Bezeichnung <- ifelse(heterosk, "Heteroskedastie", "Homoskedastie")
  ergebnisse <- dplyr::tibble(
    b1_coef=schaetzung_b1,
    b1_stdf=stdfehler_b1,
    Fall=rep(Fall_Bezeichnung, 
             n_stichproben)
  )
return(ergebnisse)
}

Damit können wir die Simulation sehr einfach für die beiden relevanten Fälle ausführen.

Wir definieren nun die Parameter und die wahren Werte. Hierbei ist es wichtig, die Funktion set.seed zu verwenden. Das ist wichtig um unsere Monte Carlo Simulation reproduzierbar zu machen, denn mit set.seed setzen wir die Anfangsbedingungen für den Zufallszahlen-Generator von R. Das bedeutet, dass wir für den gleichen Seed immer die gleichen Zufallszahlen produzieren und somit unsere Simulationsergebnisse immer vollständig reproduzierbar bleiben.

set.seed("1234")
n_stichproben <- 250
n_beobachtungen <- 1000
x_data <- runif(n = n_beobachtungen, min = 1, max = 10)
wahres_b0 <- 1
wahres_b1 <- 2
schaetzgleichung <- as.formula("y~x1")

set.seed("1234")
homosc_results <- mcs(1000, x_data,
                      wahres_b0, wahres_b1, 
                      schaetzgleichung, heterosk = F)
hetero_results <- mcs(1000, x_data,
                      wahres_b0, wahres_b1,
                      schaetzgleichung, heterosk = T)
full_results <- rbind(homosc_results, hetero_results)

4. Schritt: Vergleichende Analyse der Schätzereigenschaften

Als erstes wollen wir die Ergebnisse grafisch analysieren. Zu diesem Zweck visualisieren wir in Abbildung 11.5 die Verteilung der geschätzten Werte für \(\beta_1\) und zeichnen zudem den wahren Wert ein:

beta_1_plot <- ggplot2::ggplot(data = full_results, 
                      mapping = aes(x=b1_coef, color=Fall, fill=Fall)) +
  ggplot2::geom_density(alpha=0.5) +
  ggplot2::scale_y_continuous(expand = expansion(c(0, 0), c(0, 0.05))) +
  ggplot2::scale_x_continuous(limits = c(1.9, 2.1), expand = c(0,0)) +
  ggplot2::geom_vline(xintercept = wahres_b1) +
  ggplot2::ylab(TeX("Dichte von $\\hat{\\beta}_1$")) +
  ggplot2::xlab(TeX("$\\hat{\\beta}_1$")) +
  ggplot2::ggtitle(TeX("Verteilung von $\\hat{\\beta}_1$")) +
  ggplot2::scale_color_manual(values = c("Homoskedastie"="#006600",
                                "Heteroskedastie"="#800000"),
  aesthetics = c("color", "fill")) +
  icaeDesign::theme_icae()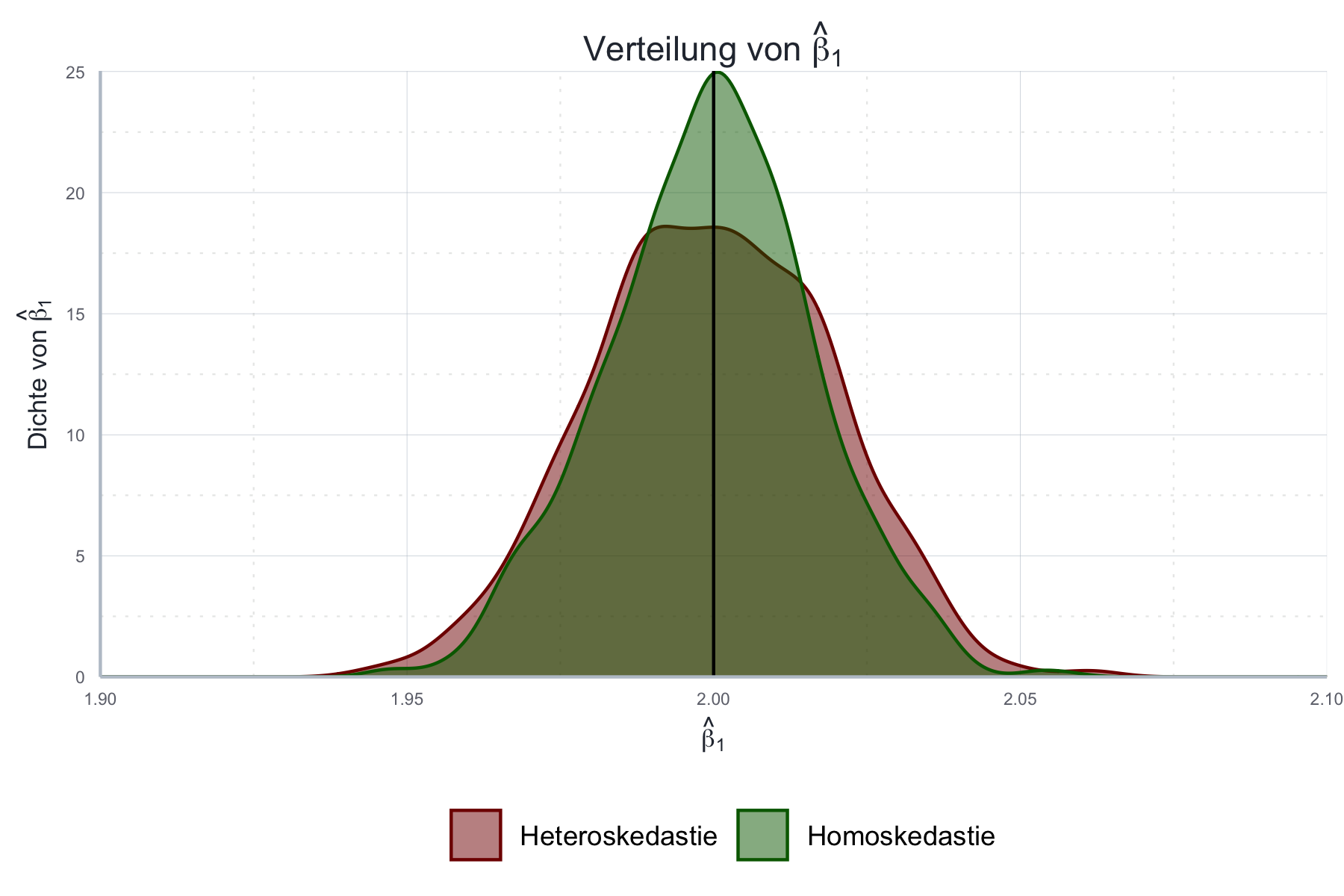

Abbildung 11.5: Vergleich der Verteilung der mit Monte Carlo geschätzten Werte für \(\beta_1\) mit dem wahren Wert.

Wie wir sehen ändert die Verletzung der Homoskedastie-Annahme nichts an der Erwartungstreue des Schätzers: im Mittel trifft der Schätzer den wahren Wert \(\beta_1\)! Allerdings nimmt die Genauigkeit ab, da die Streuung um den wahren Wert herum im heteroskedastischen Fall zunimmt!

Wir wollen nun in Abbildung 11.6 noch untersuchen wie sich Heteroskedastie auf die Standardfehler der Regression auswirkt.

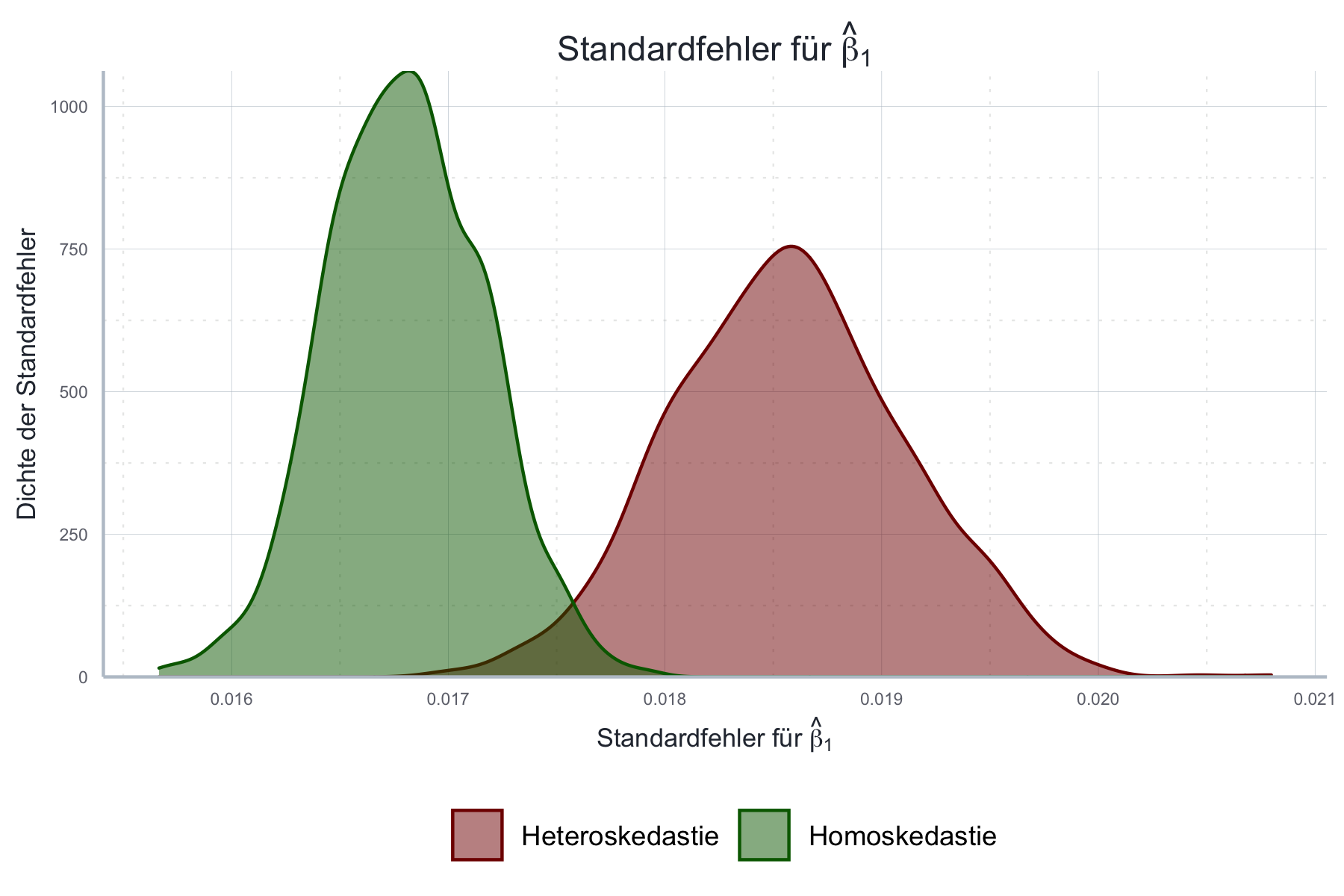
Abbildung 11.6: Vergleich der Standardfehler von \(\hat{\boldsymbol{\beta}}\) bei Homoskedastie und Heteroskedastie.

Wie wir sehen weichen die Standardfehler im heteroskedastischen Fall deutlich von denen im homoskedastischen Fall ab! Welche Standardfehler sind nun die richtigen?

Ohne auf die mathematische Herleitung genauer einzugehen (siehe dazu Kapitel 4 in Greene (2018)) wollen wir dennoch festhalten, dass die geschätzten Standardfehler unter Heteroskedastie falsch sind. Wir können ohne eine Korrektur also keine Aussagen über die Schätzunsicherheit und Signifikanz der Ergebnisse treffen.

Das alles bedeutet zwar, dass der OLS Schätzer auch im Falle von Heteroskedastie noch erwartungstreu ist, allerdings die Genauigkeit des Schätzers sinkt und die Standardfehler falsch berechnet werden. Da der Fokus hier auf der Beschreibung der Monte Carlo Simulationsmethode lag werden wir uns mit den möglichen Lösungen erst später befassen.

Im Folgenden werden wir nun einen weiteren Blick auf verschiedene OLS Annahmen werfen und besprechen wie die jeweilige Annahme geprüft werden kann und was im Falle einer Verletzung zu tun wäre.

11.2 Heteroskedastie

Wie oben beschrieben bedeutet Heteroskedastie, dass die Varianz der Fehlerterme nicht konstant ist.

11.2.1 Liegt Heteroskedastie vor?

Heteroskedastie kann grafisch oder über statistische Tests identifiziert werden. Um Heteroskedastie grafisch zu identifizieren verwenden wir den Tukey-Anscombe-Plot, in dem wir auf der x-Achse die gefitteten Werte \(\hat{Y}\) und auf der y-Achse die Residuen \(e\) abbilden. Siehe dazu Abbildung 11.7. Für die Konstruktion der Abbildung sollten Sie beachten, dass die gefitteten Werte und die Residuen einer Schätzung immer im der durch lm() produzierten Liste gespeichert werden. Gehen wir mal davon aus, dass Sie Ihr Schätzobjekt folgendermaßen definiert haben:

schaetzung <- lm(y ~ x + y, data = daten)

Dann können Sie auf die gefitteten Werte \(\hat{Y}\) über schaetzung[["fitted.values"]] und auf die Residuen über schaetzung[["residuals"]] zugreifen.

Warum überhaupt eine Residuenanalyse? Die Residuen werden häufig herangezogen wenn es um die Überprüfung der OLS-Annahmen geht. Letztere beziehen sich nämlich insbesondere auf die Fehlerterme des Modells. Da die Fehlerterme jedoch eine Populationsgröße sind und dementsprechend nicht beobachtbar sind, nehmen wir häufig ihr Stichproben-Pendant um die Annahmen zu überprüfen - und dieses Stichproben-Pendant sind eben die Residuen. Dennoch ist es extrem wichtig nie zu vergessen, dass die Residuen nur eine Approximation der Fehler sind und es durchaus der Fall sein kann, dass die Residuen nicht auffällig sind, aber dennoch eine Annahme über die Fehler nicht erfüllt sein kann.

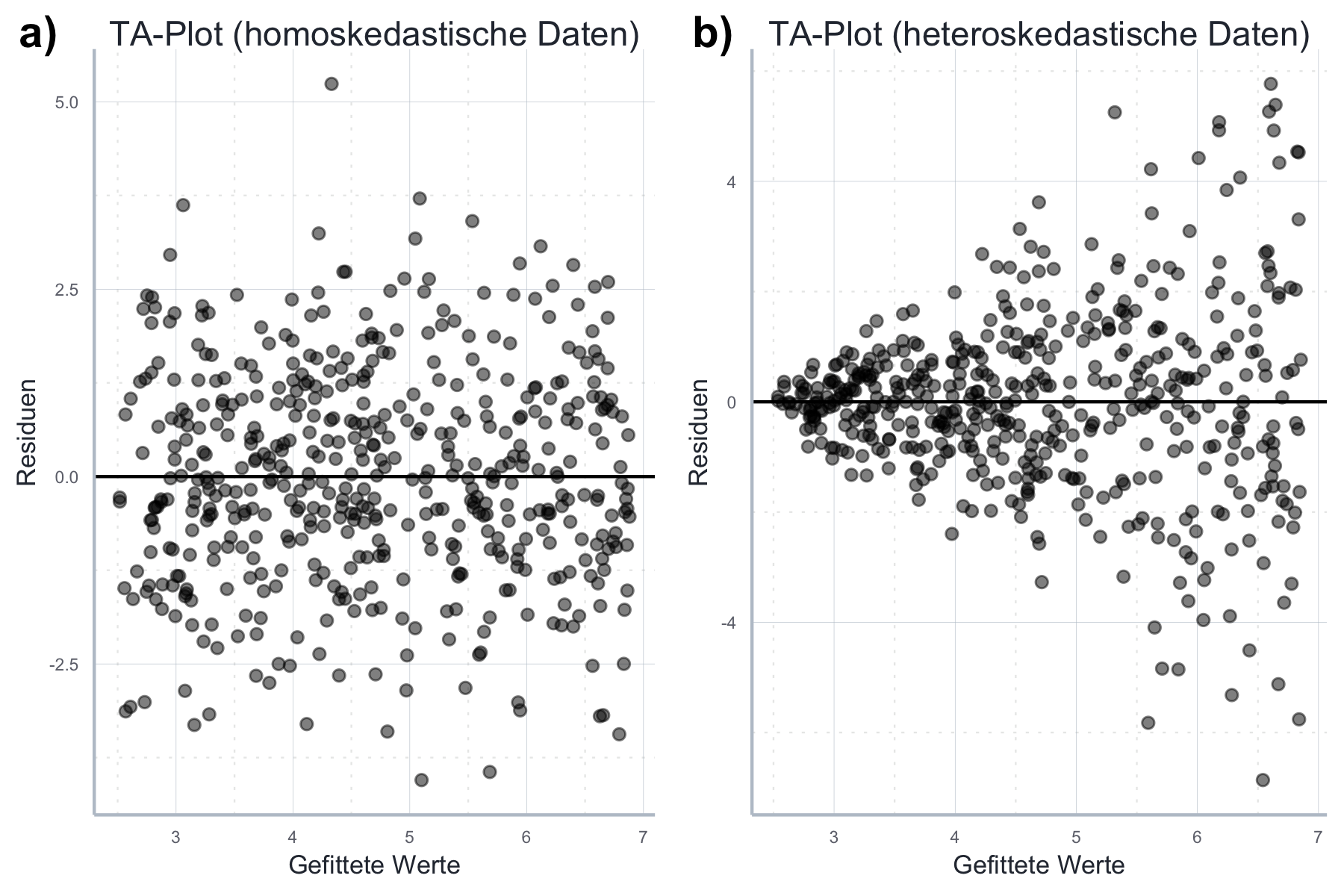
Abbildung 11.7: Graphische Analyse der Homoskedastie.

Im Optimalfall ist die Varianz der Residuen konstant. Das scheint in Abbildung (a) der Fall zu sein: die Residuen streuen recht zufällig um die Mittelwert 0 herum. In diesem Fall besteht wenig Grund zur Annahme, dass Heteroskedastizität vorliegt. Anders in Abbildung (b): hier wird die Varianz nach rechts klar größer. Das lässt große Zweifel an der Annahme der Homoskedastizität aufkommen. Denn wenn die Residuen keine konstante Varianz aufweisen tun es die Fehler wahrscheinlich auch nicht.

In der Praxis ist es sinnvoll zusätzlich zur grafischen Inspektion noch statistische Tests zu verwenden. Hier gibt es ein breites Angebot an Tests. Viele davon sind in dem Paket lmtest (Zeileis und Hothorn 2002) gesammelt. Wir gehen auf die mathematische Herleitung der Tests hier nicht ein. Genauere Informationen finden Sie in den später angegebenen weiterführenden Quellen.

Häufig verwendet wird z.B. der Breusch-Pagan Test, den wir mit der Funktion bptest() durchführen können. Diese Funktion nimmt als einziges zwingendes Argument das Regressionsobjekt. Die weiteren Argumente sollten wir im Normalfall auf den Standardwerten belassen.

Die Nullhypothese des Breusch-Pagan Tests ist Homoskedastie. Wir führen zunächst den Test für den homoskedastischen Fall aus, wobei schaetzung_homo das von lm() produzierte Objekt ist:

bptest(schaetzung_homo)

#> 
#>  studentized Breusch-Pagan test
#> 
#> data:  schaetzung_homo
#> BP = 0.0067387, df = 1, p-value = 0.9346

Wir können \(H_0\) (also die Hypothese der Homoskedastie) nicht ablehnen da \(p>0.05\). Nun führen wir den Test für den heteroskedastischen Fall aus:

bptest(schaetzung_hetero)

#> 
#>  studentized Breusch-Pagan test
#> 
#> data:  schaetzung_hetero
#> BP = 88.513, df = 1, p-value < 2.2e-16

Wir können \(H_0\) (also die Hypothese der Homoskedastie) hier klar ablehnen.

Ein ebenfalls häufig verwendeter Test ist der Goldfeld-Quandt Test. Dieser wird mit der Funktion gqtest() durchgeführt und hat mehr Freiheitsgrade als der Breusch-Pagan Test: hier testen wir die Hypothese ob die Fehlervarianz in einem Bereich der Daten größer oder kleiner ist als in einem anderen Bereich. Standardmäßig wird der Datensatz dabei in zwei gleich große Teile geteilt, aber der Trennpunkt kann mit dem Argument point theoretisch beliebig gewählt werden, genauso wie der Anteil der Daten um den Trennpunkt, die ausgeschlossen werden sollen (Argument fraction). Zudem können wir über das Argument alternative wählen ob für steigende, sinkende oder andere Varianz getestet werden soll. Diese Wahlmöglichkeiten erhöhen die Power des Tests - wenn wir denn theoretisch gut begründete Werte wählen können. Ansonsten ist es am besten die Standardwerte zu verwenden und den Test mit anderen Tests und grafischen Methoden zu ergänzen.

Wir verwenden zunächst den Test mit der Standardspezifikation:

gqtest(schaetzung_homo)

#> 
#>  Goldfeld-Quandt test
#> 
#> data:  schaetzung_homo
#> GQ = 0.98576, df1 = 248, df2 = 248, p-value = 0.5449
#> alternative hypothesis: variance increases from segment 1 to 2

Für den homoskedastischen Fall kann \(H_0\) (Homoskedastie) also nicht abgelehnt werden.

gqtest(schaetzung_hetero)

#> 
#>  Goldfeld-Quandt test
#> 
#> data:  schaetzung_hetero
#> GQ = 0.79606, df1 = 248, df2 = 248, p-value = 0.9635
#> alternative hypothesis: variance increases from segment 1 to 2

Komischerweise muss \(H_0\) auch für den heteroskedastischen Fall nicht verworfen werden. Hätten wir aber für sinkende Varianz getestet, hätte \(H_0\) abgelehnt werden können:

gqtest(schaetzung_hetero, alternative = "less")

#> 
#>  Goldfeld-Quandt test
#> 
#> data:  schaetzung_hetero
#> GQ = 0.79606, df1 = 248, df2 = 248, p-value = 0.03655
#> alternative hypothesis: variance decreases from segment 1 to 2

Das zeigt die potenzielle Schwäche des GQ-Tests. Wenn wir uns nicht sicher sind ob wir für steigende oder sinkende Varianz testen sollen bietet sich natürlich immer auch der zweiseitige Test an, der aber über eine verminderte Power vefügt, im vorliegenden Falle aber dennoch das richtige Ergebnis liefert:

gqtest(schaetzung_hetero, alternative = "two.sided")

#> 
#>  Goldfeld-Quandt test
#> 
#> data:  schaetzung_hetero
#> GQ = 0.79606, df1 = 248, df2 = 248, p-value = 0.0731
#> alternative hypothesis: variance changes from segment 1 to 2

Wir lernen aus diesen Ergebnissen, dass wir immer mit verschiedenen Methoden auf Heteroskedastie testen sollten und immer sowohl grafische als auch quantitative Tests verwenden sollten. Für den Fall, dass unsere Daten Heteroskedastie aufweisen sollte dann eine der im folgenden beschriebenen Strategien als Reaktion auf Heteroskedastie umgesetzt werden.

11.2.2 Reaktionen auf Heteroskedastie

Aus unseren Vorüberlegungen können wir Folgendes festhalten:

1. Der OLS-Schätzer ist auch unter Heteroskedastie erwartungstreu
2. Der OLS-Schätzer ist weiterhin konsistent
3. Die Varianz des OLS-Schätzers ist unter Heteroskedastie größer und der Schätzer ist nicht mehr effizient
4. Die Standardfehler unter Heteroskedastie sind nicht mehr korrekt.

Daraus ergibt sich, dass wir in jedem Fall die Standardfehler korrigieren müssen. Darüber hinaus können wir uns überlegen ob wir es bei der Korrektur belassen und die geschätzten Werte des Standard OLS-Schätzers weiterhin verwenden, da der Schätzer ja weiterhin erwartungstreu und konsistent ist, oder ob wir sogar gleich ein alternatives Schätzverfahren implementieren um die Effizienz des Schätzers zu steigern.

Für den ersten Fall korrigieren wir ‘einfach’ die Standardfehler des OLS-Schätzers, verwenden aber die alten geschätzten Koeffizienten weiter. Im zweiten Fall verwenden wir die Schätzmethode der Generalized Least Squares um nicht nur die Standardfehler zu korrigieren sondern auch die Parameter neu zu schätzen.

Welchen Fall sollten wir verwenden? Wie gesagt ist der OLS Schätzer weiterhin konsistent. Das bedeutet, dass wir in großen Stichproben eigentlich kein Problem haben. In kleinen Stichproben kann die Verwendung dagegen Effizienzverluste mit sich bringen - aber keinen Verlust der Erwartungstreue. Beim GLS Verfahren schätzen wir die Varianzstruktur. Das funktioniert gut, wenn wir große Stichproben haben. Gerade da ist aber die Verwendung der OLS Schätzers aufgrund seiner Konsistenz gar kein Problem. In kleinen Stichproben ist die Schätzung der Varianz dagegen problematisch, solange wir keine theoretischen Restriktionen einführen können. Insofern ist die sinnvolle Anwendung von GLS eher gering, weswegen wir uns im Folgenden darauf beschränken robuste Standardfehler einzuführen.

Die am weitesten verbreitete Korrektur der Standardfehler sind White’s robuste Standardfehler.⁹⁴ Um diese in R zu berechnen bedarf es zweier Schritte. Zunächst verwenden wir die Funktion vcovHC() aus dem Paket sandwich (Zeileis 2004) um eine korrigierte Varianz-Kovarianz-Matrix zu berechnen. Diese Funktion nimmt als notwendiges Argument das Regressionsobjekt. Darüber hinaus können wir über das Argument type die genaue Berechnungsmethode festlegen. Mehr Infos dazu findet sich z.B. in der Hilfefunktion. Hier verwenden wir die am häufigsten verwendete Verion "HC1":

var_covar_matrix <- vcovHC(schaetzung_hetero, type = "HC1")
var_covar_matrix

#>              (Intercept)           x1
#> (Intercept)  0.018596906 -0.004287583
#> x1          -0.004287583  0.001130885

Dann können wir die Funktion coeftest() aus dem Paket lmtest verwenden um die korrigierten Standardfehler zu erhalten:

coeftest(schaetzung_hetero, vcov. = var_covar_matrix)

#> 
#> t test of coefficients:
#> 
#>             Estimate Std. Error t value  Pr(>|t|)    
#> (Intercept) 2.047718   0.136370  15.016 < 2.2e-16 ***
#> x1          0.482333   0.033629  14.343 < 2.2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Diese unterscheiden sich offensichtlich von den nicht-korrigierten Standardfehlern:

summary(schaetzung_hetero)

#> 
#> Call:
#> lm(formula = schaetzgleichung, data = stichprobe_hetero)
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -6.8628 -0.8143 -0.0055  0.7927  5.7683 
#> 
#> Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)   2.0477     0.1753   11.68   <2e-16 ***
#> x1            0.4823     0.0291   16.58   <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 1.657 on 498 degrees of freedom
#> Multiple R-squared:  0.3556, Adjusted R-squared:  0.3543 
#> F-statistic: 274.8 on 1 and 498 DF,  p-value: < 2.2e-16

Beachten Sie, dass die korrigierten Standardfehler zwar häufig größer sind, dies aber nicht notwendigerweise der Fall sein muss!

11.3 Autokorrelation

Wir sprechen von Autokorrelation wenn die Fehlerterme in der Regression untereinander korreliert sind. Wie bei der Heteroskedastizität ist die Varianz-Kovarianz Matrix eine andere als ursprünglich angenommen: im Falle der Heteroskedastizität lag die Abweichung auf der Hauptdiagonalen, also der Varianz der einzelnen Fehlerterme, die nicht wie laut A4 konstant ist. Im Falle der Autokorrelation liegt das Problem abseits der Hauptdiagonale, bei den Kovarianzen der einzelnen Fehler. Standardmäßig nehmen wir an, dass diese Kovarianz gleich Null ist, in der Praxis ist diese Annahme möglicherweise nicht erfüllt.

Besonders häufig tritt Autokorrelation auf, wenn wir mit Zeitreihendaten arbeiten. Denn dann ist es sogar sehr plausibel, dass die Fehler einer Beobachtung in \(t\) mit denen aus der Vorperiode \(t-1\) zusammenhängen. Entsprechend groß ist die Literatur zur Autokorrelation in der Zeitreihenanalyse und Panel-Schätzung. Auch wenn Zeitreihenanalysen und Panel-Schätzungen hier nicht weiterführend diskutiert werden ist es hilfreich sich die Folgen von Autokorrelation auch jetzt schon anzusehen.

11.3.1 Folgen von Autokorrelation

Wir wissen zwar von der Herleitung des OLS-Schätzers bereits, dass Autokorrelation keinen Einfluss auf die Erwartungstreue des Schätzers hat, wir wollen aber dennoch die Folgen von Autokorrelation durch eine kleine Monte Carlo Simulation (MCS) illustrieren.

Dazu erstellen wir zunächst einen künstlichen Datensatz in dem die Fehler unterschiedlich stark miteinander korreliert sind. Um die Variablen mit vorher spezifizierter Korrelation zu erstellen verwenden wir wieder die Funktion mvrnorm aus dem Paket MASS (Venables und Ripley 2002). Eine genauere Erläuterung findet sich hier. Das Ergebnis der Simulation lässt sich in Abbildung 11.8 ablesen.

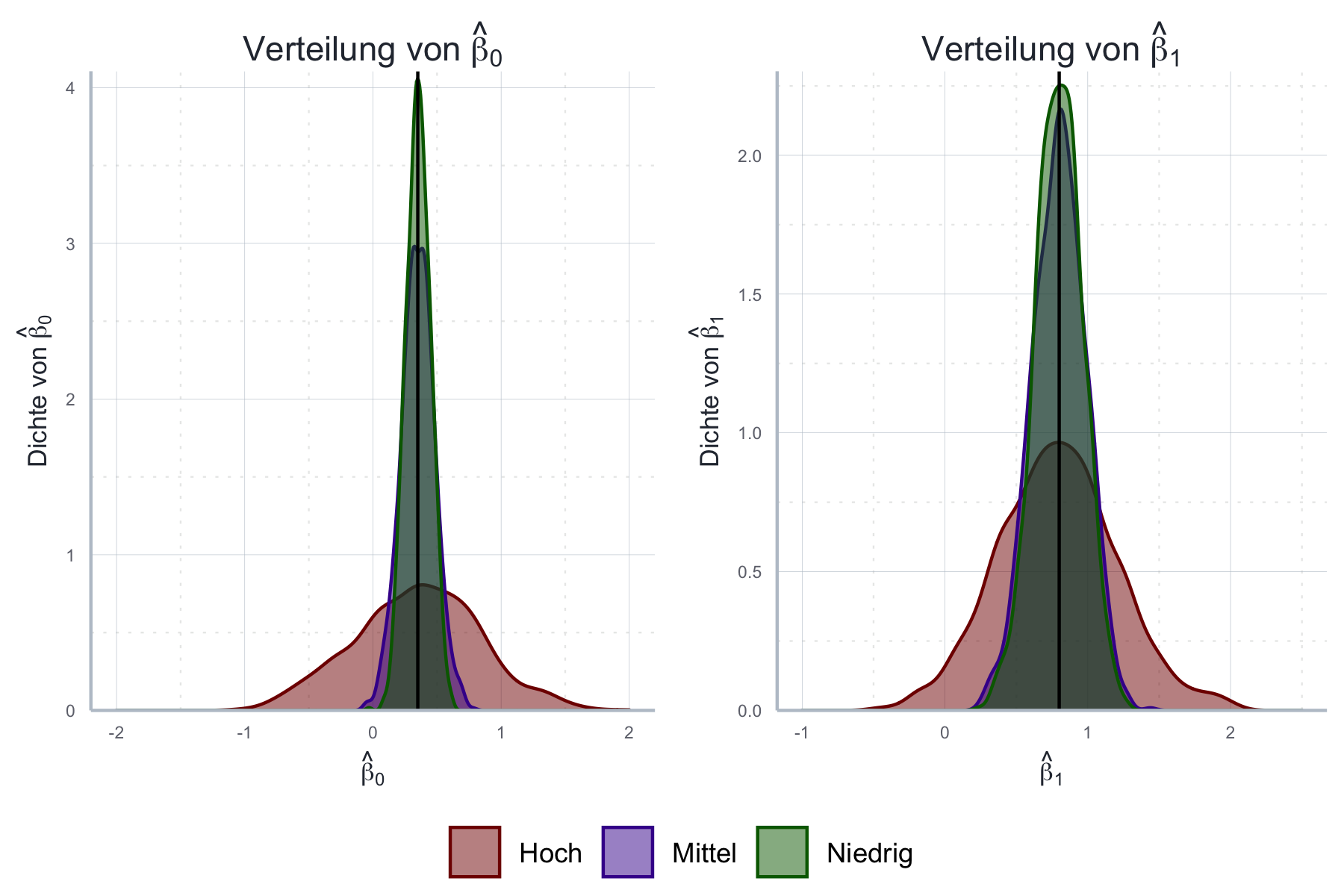
Abbildung 11.8: Folgen der Autokorrelation mit Bezug auf Erwartungstreue und Effizienz anhand von Monte Carlo Simulationen.

Wie erwartet bleiben die Schätzer erwartungstreu, büßen aber deutlich an Effizienz ein wenn die Autokorrelation größer wird. Betrachten wir nun noch die geschätzten Standardfehler in Abbildung 11.9.

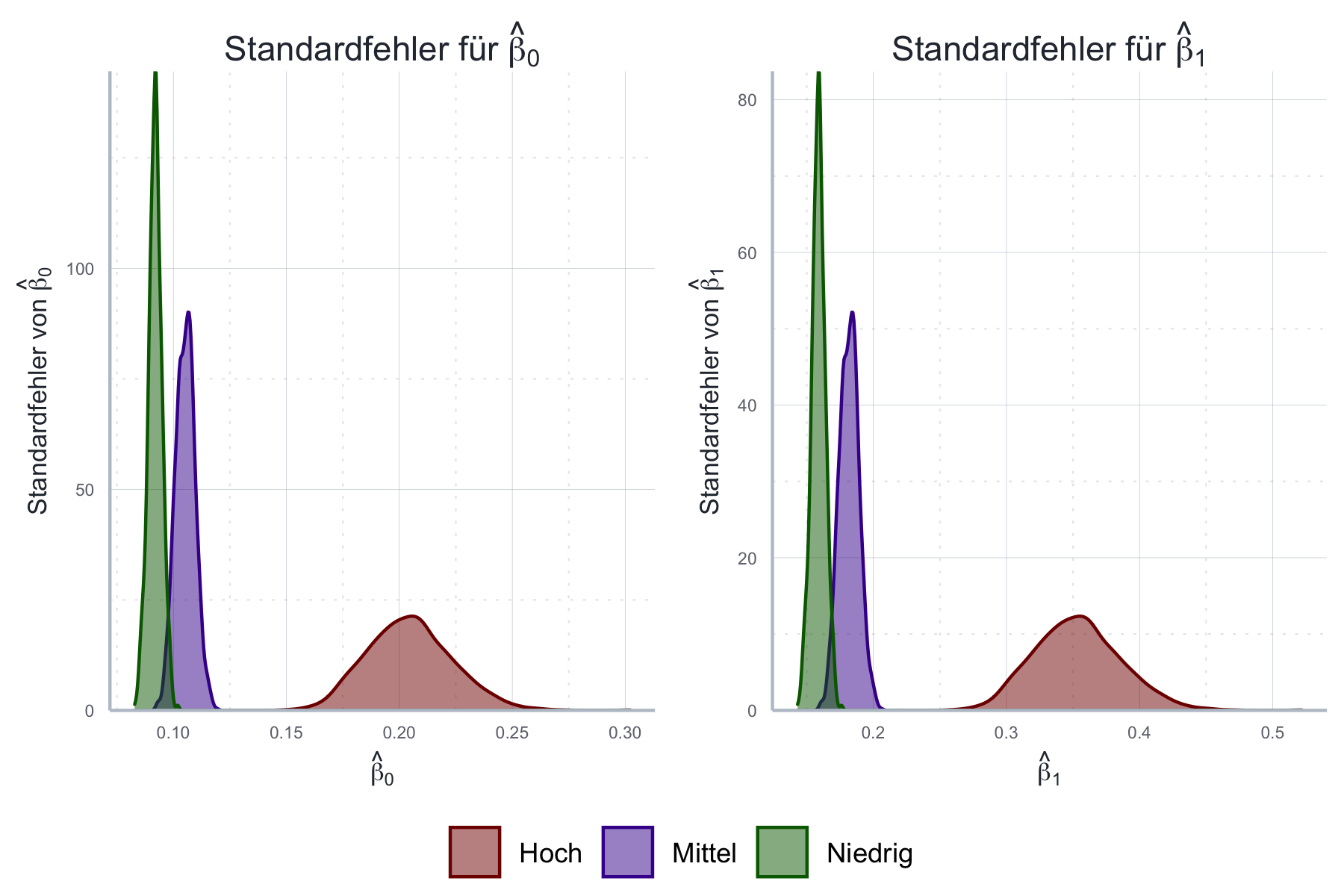
Abbildung 11.9: Folgen der Autokorrelation mit Bezug auf Standardfehler anhand von Monte Carlo Simulationen.

Wie bei der Heteroskedastie hat Autokorrelation einen großen Einfluss auf die geschätzten Standardfehler. Da auch hier geschätzten Standardfehler falsch sind müssen wir entsprechend kontrollieren.

11.3.2 Testen auf Autokorrelation

Wie bei der Heteroskedastie sollten wir auch beim Testen auf Autokorrelation grafische und quantitative Tests kombinieren. Für die grafische Analyse verwenden wir wie vorher den Tukey-Anscombe Plot der Residuen (siehe Abschnitt 11.2.1). Die Idee ist, dass wenn in den ‘echten’ Fehlern Autokorrelation vorherrscht wir das auch in den Residuen beobachten können. Abbildung 11.10 verdeutlicht, wie wir Autokorrelation in den entsprechenden Abbildungen erkennen können.

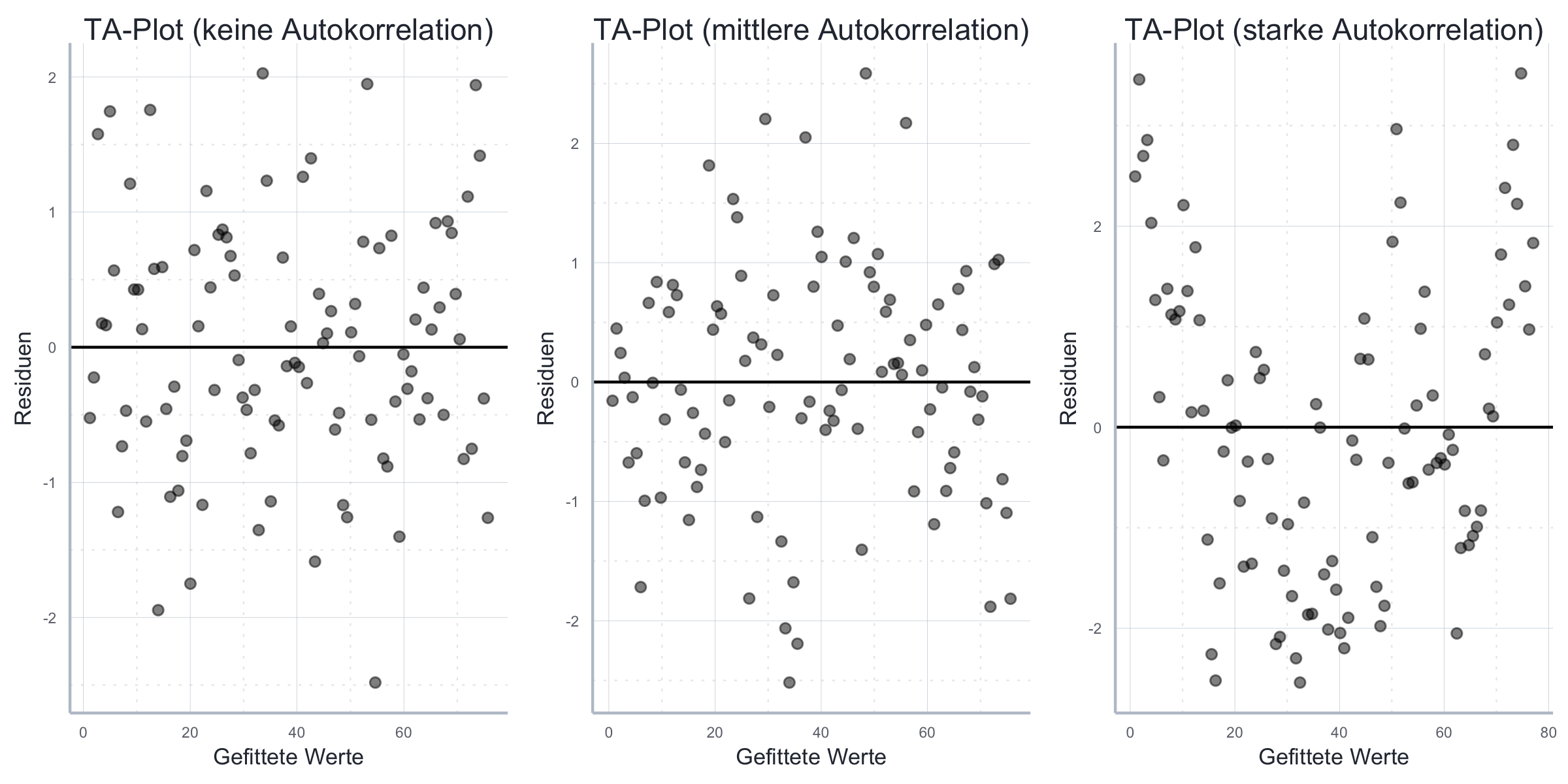
Abbildung 11.10: Unterschiedlich starke Autokorrelation im Tukey-Anscombe Plot.

Gerade bei Anwendungen außerhalb der Zeitreihenökonometrie ist Autokorrelation aber grafisch nicht so einfach zu identifizieren. Dennoch ist gerade bei der starken Autokorrelation offensichtlich, dass die Kovarianz der Fehler nicht gleich Null ist.

Die vielen Arten von Autokorrelation Das Problem beim Testen auf Autokorrelation ist, dass die Fehler natürlich auf sehr viele Arten miteinander korreliert sein können. In Zeitreihen beobachten wir häufig einen so genannten autoregressiven Prozess, bei dem die Fehler in \(t\) folgendermaßen bestimmt sind: \(\epsilon_t=\rho\epsilon_{t-1}+u\), wobei \(u\propto\mathcal{N}(0,\sigma^2)\). Es sind aber natürlich viele weitere Möglichkeiten denkbar, was es schwierig macht allgemeine Tests für Autokorrelation zu entwickeln. Wenn wir aufgrund von theoretischen Überlegungen eine bestimmte Struktur der Autokorrelation vermuten, können wir spezialisierte Tests verwenden, die über deutlich größere Power verfügen als allgemeine Tests.

Es gibt diverse Tests für Autokorrelation, die für jeweils unterschiedliche Settings besonders gut oder weniger gut geeignet sind. Insofern macht es Sinn sich für den konkreten Anwendungsfall die am besten passenden Tests herauszusuchen und immer mehr als einen Test zu verwenden. Im Folgenden werden einige prominente Tests vorgestellt.

Häufig verwendet wird der Box–Pierce, bzw. Ljung–Box Test, welche die \(H_0\) keiner Autokorrelation testen. Sie unterscheiden sich in der genauen Berechnung der Teststatistik und können als Alternativhypothese eine Autokorrelation von unterschiedlichen Graden testen. Mit unterschiedlichen Graden meinen wir die Anzahl der Lags, also der Verzögerungen, zwischen den Beobachtungen, deren Fehler noch miteinander korreliert sind. Standardmäßig testen wir gegen eine Autokorrelation mit Grad 1, allerdings können je nach Anwendungsfall auch höhere Grade sinnvoll sein.

Die Funktion Box.test() kann verwendet werden um diese Tests durchzuführen. Das erste Argument sind immer die Residuen der zu untersuchenden Regression, mit dem Argument type wird dann der Test ("Box-Pierce" oder "Ljung-Box") ausgewählt und mit lag der Grad der Autokorrelation. Entsprechend testen wir folgendermaßen auf eine Autokorrelation mit Grad 1:

Box.test(mid_acl$residuals, lag = 1, type = "Box-Pierce")

#> 
#>  Box-Pierce test
#> 
#> data:  mid_acl$residuals
#> X-squared = 9.5899, df = 1, p-value = 0.001957

bzw.:

Box.test(mid_acl$residuals, lag = 1, type = "Ljung-Box")

#> 
#>  Box-Ljung test
#> 
#> data:  mid_acl$residuals
#> X-squared = 9.8805, df = 1, p-value = 0.00167

In beiden Fällen muss \(H_0\) abgelehnt werden. Wir müssen also von Autokorrelation ausgehen!

Ein anderer bekannter Test auf Autokorrelation ist der Durbin-Watson Test, der allerdings nicht besonders robust ist. Wir können diesen Test mit der Funktion dwtest() aus dem Paket lmtest implementieren. Dazu übergeben wir als erstes Argument das Schätzobjekt der zu überprüfenden Schätzung:

dwtest(small_acl)

#> 
#>  Durbin-Watson test
#> 
#> data:  small_acl
#> DW = 1.9569, p-value = 0.3741
#> alternative hypothesis: true autocorrelation is greater than 0

\(H_0\) des DW-Tests ist keine Autokorrelation. Im aktuellen Fall können wir \(H_0\) (keine Autokorrelation) nicht ablehnen und wir brauchen uns keine Gedanken über Autokorrelation machen. Allerdings können wir die Alternativhypothese des Tests selbst über das Argument alternative festlegen. Wir haben dabei die Wahl zwischen verschiedenen Strukturen der Autokorrelation, nämlich ob die Fehler in zukünftigen Beobachtungen positive (alternative="greater") oder negativ (alternative="less") von dem Fehler in der aktuellen Beobachtung abhängen. Sind wir uns unsicher wählen wir am besten einen zweiseitigen Test (alternative="two.sided"). Wie immer ist die Power des Tests größer wenn wir \(H_1\) restriktiver wählen.

Im folgenden Beispiel ist die tatsächliche Autokorrelation positiv. Die Rolle der gewählten \(H_1\) wird so deutlich:

dwtest(mid_acl, alternative = "greater")

#> 
#>  Durbin-Watson test
#> 
#> data:  mid_acl
#> DW = 1.3469, p-value = 0.0003333
#> alternative hypothesis: true autocorrelation is greater than 0

Hier gibt der Test also korrektermaßen Autokorrelation an. Testen wir dagegen gegen die ‘falsche’ \(H_1\):

dwtest(mid_acl, alternative = "less")

#> 
#>  Durbin-Watson test
#> 
#> data:  mid_acl
#> DW = 1.3469, p-value = 0.9997
#> alternative hypothesis: true autocorrelation is less than 0

In diesem Fall wird keine entsprechende Autokorrelation gefunden. Im Zweifel ist daher der zweiseitige Test vorzuziehen:

dwtest(mid_acl, alternative = "two.sided")

#> 
#>  Durbin-Watson test
#> 
#> data:  mid_acl
#> DW = 1.3469, p-value = 0.0006667
#> alternative hypothesis: true autocorrelation is not 0

Hier wird \(H_0\) wieder korrektermaßen verworfen.

Zuletzt wollen wir noch den Breusch-Godfrey Test einführen, der als relativ robust und breit anwendbar gilt. Er wird mit der Funktion bgtest() aus dem Pakelt lmtest durchgeführt. Hier wird als erstes Argument wieder das Regressionsobjekt übergeben. Als Spezifikationsalternativen können wir wiederum den höchsten Grad der zu testenden Autokorrelation (Argument order) und die Art der Teststatisik (Argument type) auswählen.

Zum Beispiel:

bgtest(mid_acl, order = 1, type = "F")

#> 
#>  Breusch-Godfrey test for serial correlation of order up to 1
#> 
#> data:  mid_acl
#> LM test = 10.702, df1 = 1, df2 = 97, p-value = 0.001483

Oder:

bgtest(mid_acl, order = 1, type = "Chisq")

#> 
#>  Breusch-Godfrey test for serial correlation of order up to 1
#> 
#> data:  mid_acl
#> LM test = 9.9367, df = 1, p-value = 0.00162

Insgesamt bedarf die richtige Wahl des Tests einige theoretische Überlegungen für den Anwendungsfall und wir sollten uns nicht auf das Ergebnis eines einzelnen Tests verlassen!

11.3.3 Reaktionen auf Autokorrelation

Falls wir Autokorrelation in den Residuen finden sollten wir aktiv werden und die Standardfehler unserer Schätzung äquivalent zur Heteroskedastie korrigieren. Da der Schätzer selbt weiterhin erwartungstreu ist können wir die OLS-Schätzer als solche weiterverwenden. Effizienzgewinne sind durch alternative Schätzverfahren möglich, werden hier aber nicht weiter verfolgt.

Das Vorgehen ist dabei quasi äquivalent zum Fall der Heteroskedastie. Wir berechnen wieder zunächst eine robuste Varianz-Kovarianzmatrix mit der Funktion vcovHAC() aus dem Paket sandwich und korrigieren dann die Standardfehler mit der Funktion coeftest() and dem Paket lmtest. Beachten Sie, dass die resultierenden Standardfehler robust sowohl gegen Heteroskedastie als auch Autokorrelation sind.

var_covar_matrix <- vcovHAC(large_acl) 
coeftest(large_acl, vcov. = var_covar_matrix)

#> 
#> t test of coefficients:
#> 
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept) 0.186245   0.919704  0.2025   0.8399    
#> x           0.768353   0.015084 50.9371   <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Diese unterscheiden sich offensichtlich von den nicht-korrigierten Standardfehlern:

summary(large_acl)

#> 
#> Call:
#> lm(formula = y ~ x, data = dgp_acl(0.5, 0.75, 1:100, 0.85))
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -2.5399 -1.1799 -0.1028  1.0744  3.5191 
#> 
#> Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept) 0.186245   0.304383   0.612    0.542    
#> x           0.768353   0.005233 146.833   <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 1.511 on 98 degrees of freedom
#> Multiple R-squared:  0.9955, Adjusted R-squared:  0.9954 
#> F-statistic: 2.156e+04 on 1 and 98 DF,  p-value: < 2.2e-16

11.4 Multikollinearität

In den OLS-Annahmen schließen wir lediglich perfekte Multikollinearität aus. Diese läge vor, wenn eine erklärende Variable eine lineare Funktion einer anderen erklärenden Variable wäre. Da wir in diesem Falle die Matrix \(\boldsymbol{X}\) in der Formel für \(\boldsymbol{\hat{\beta}}\) nicht invertierbar, wir können \(\boldsymbol{X'X\hat{\beta}}=\boldsymbol{X'Y}\) also nicht berechnen und der OLS Schätzer ist überhaupt nicht identifizierbar.

Es zeigt sich jedoch, dass bereits die Existenz von moderater Multikollinearität wichtige Implikationen für den OLS Schätzer hat. Wir sprechen von moderater Multikollinearität wenn zwei oder mehrere erklärende Variablen miteinander korrelieren. Wie wir sehen werden nimmt in diesem Falle die Schätzgenauigkeit ab, weswegen man die Inklusion stark miteinander korrlierter erklärenden Variablen vermeiden sollte.

11.4.1 Folgen von Multikollinearität

Gehen wir einmal von folgender Regressionsgleichung aus:

\[Y_i = \hat{\beta}_0 + \hat{\beta}_1 x_{i1} + \hat{\beta}_2 x_{i2} + e\]

Zunächst wollen wir den Effekt von Multikollinearität per Monte Carlo Simulation ergründen. Zu diesem Zweck erstellen wir drei Datensätze: einen mit wenig, einen mit mittel und einen mit stark korrelierten erklärenden Variablen. Davon abgesehen bleiben die OLS Annahmen erfüllt. Um die Variablen mit vorher spezifizierter Korrelation zu erstellen verwenden wir wieder die Funktion mvrnorm aus dem Paket MASS (Venables und Ripley 2002). Eine genauere Erläuterung findet sich hier.

set.seed("123")
stichprobengroesse <- 500
r_small <- 0.0
r_mid <- 0.4
r_large <- 0.9

data_small = mvrnorm(n=stichprobengroesse, mu=c(0, 0), 
                     Sigma=matrix(c(1, r_small, r_small, 1), 
                                  nrow=2), empirical=TRUE)

data_mid = mvrnorm(n=stichprobengroesse, mu=c(0, 0), 
                   Sigma=matrix(c(1, r_mid, r_mid, 1), 
                                nrow=2), empirical=TRUE)

data_large = mvrnorm(n=stichprobengroesse, mu=c(0, 0), 
                     Sigma=matrix(c(1, r_large, r_large, 1), 
                                  nrow=2), empirical=TRUE)

x_1_small = data_small[, 1]  
x_1_mid = data_mid[, 1]  
x_1_large = data_large[, 1]  

x_2_small = data_small[, 2]  
x_2_mid = data_mid[, 2]  
x_2_large = data_large[, 2]  

cor(x_1_small, x_2_small)  # Test

#> [1] 5.082293e-17

cor(x_1_mid, x_2_mid)  # Test

#> [1] 0.4

cor(x_1_large, x_2_large)  # Test

#> [1] 0.9

Analog zum Vorgehen oben führen wir nun eine Monte Carlo Simulation durch, in der wir wiederholt Stichproben aus einem künstlich generierten Datensatz ziehen und das oben beschriebene Modell mit Hilfe von OLS schätzen. Dies führt zu der in Abbildung 11.11 aufgezeigten Verteilung der Schätzer.

Abbildung 11.11: Folgen der Multikollinearität mit Bezug auf Erwartungstreue und Effizienz anhand von Monte Carlo Simulationen.

Wie wir sehen wird die Schätzgenauigkeit für die Schätzer von \(\beta_1\) und \(\beta_2\) deutlich reduziert! Auf den Schätzer des Achsenabschnitts hat Multikollinearität dagegen keinen Einfluss.

Auch analytisch kann der Effekt von Multikollinearität gezeigt werden. Betrachten wir dazu die folgenden Hilfsregressionen:

\[\begin{align} x_{i1} &= \hat{\beta}_0^a + \hat{\beta}_3^a x_{i3} + e^a\\ x_{i2} &= \hat{\beta}_0^a + \hat{\beta}_2^a x_{i1} + e^a\\ \end{align}\]

Bei \(k\) erklärenden Variablen ergeben sich die \(k-1\) Hilfsregressionen durch eine Umstellung bei der wir eine erklärende Variable auf die LHS der Regressionsgleichung ziehen und alle weiteren erklärenden Variablen auf der RHS belassen. Im Folgenden bezeichnen wir mit \(R^2_h\) das Bestimmtheitsmaß der h-ten Hilfsregression (also der Hilfsregression mit \(x_{ih}\) als abhängiger Variable).

Es kann nun gezeigt werden, dass für die Varianz des Schätzers \(\boldsymbol{\hat{\beta}}\) Folgendes gilt (siehe Greene (2018) für Details):

\[Var(\beta_h) = \frac{\sigma^2}{\left(1-R_h^2\right)\sum_{i=1}^n\left(x_{ih}-\bar{x_h}\right)^2} \] Hieraus wird unmittelbar ersichtlich, dass die Varianz des Schätzers steigt je größer das Bestimmtheitsmaß der Hilfsregressionen ist!

Gleichzeitig wissen wir aus den obigen Herleitungen auch, dass Multikollinearität keinen Einfluss auf die Erwartungstreue oder Effizienz des OLS-Schätzers hat. Beachten Sie, dass wir den Begriff Effizienz hier immer relativ verwenden: unter Multikollinearität wird der OLS-Schätzer weniger genau, aber er bleibt dennoch der genauste Schätzer, den wir zur Verfügung haben.

11.4.2 Testen auf Multikollinearität

Da der Begriff der Multikollinearität nicht exakt definiert ist (außer für den Fall der perfekten Multikollinearität) gibt es natürlich keinen exakten Test. Die Frage welches Ausmaß an Korrelation zwischen den erklärenden Variablen akzeptabel ist, ist demnach auch immer eine individuelle Entscheidung. Es haben sich jedoch einige Faustregeln herausgebildet die zumindest hilfreich sind um festzustellen ob Multikollinearität die Größe der Standardfehler in unserer Regression erklären kann.

Zu diesem Zweck führen wir wieder die Hilfsregressionen von oben durch. Die Bestimmtheitsmaße \(R^2\) dieser Hilfsregressionen geben uns einen Hinweis auf das Ausmaß der Korrelation zwischen den erklärenden Variablen. Ist eines der Bestimmtheitsmaße ähnlich groß wie das Bestimmtheitsmaß der ‘originalen’ Regression macht es Sinn sich über Multikollinearität Gedanken zu machen.

Alternativ können wir uns natürlich auch die paarweisen Korrelationen der erklärenden Variablen anschauen, allerdings berücksichtigt das nicht die Korrelation mehrerer Variablen untereinander - die Hilfsregressionen sind da der bessere Weg!

11.4.3 Reaktionen auf Multikollinearität

Grundsätzlich sollten Sie es vermeiden, stark miteinander korrlierte Variablen gemeinsam als erklärende Variablen in einer Regression zu verwenden. Gleichzeitig werden wir weiter unten sehen, dass das Weglassen von Variablen schwerwiegende Konsequenzen für die Erwartungstreue des OLS-Schätzers haben kann (Stichtwort omitted variable bias, siehe unten). Insofern müssen wir immer sehr gut überlegen ob wir eine Variable aus der Schätzgleichung eliminieren können.

Manchmal können wir die Daten transformieren um die Multikollinearität zu senken oder alternative Variablen erheben, häufig bleibt uns aber auch nichts anderes übrig als uns zu ärgern und die Kröte der Multikollinearität zu schlucken.

11.5 Vergessene Variablen

Stellen wir uns vor, der ‘wahre’ datengenerierende Prozess sähe folgendermaßen aus:

\[\boldsymbol{y} = \beta_0 + \beta_1 \boldsymbol{x}_1 + \beta_2 \boldsymbol{x}_2 + \boldsymbol{\epsilon}\]

Aufgrund geistiger Umnachtung haben wir in unserem Modell \(\boldsymbol{x}_2\) aber nicht berücksichtigt. Unser geschätztes Modell ist also:

\[\boldsymbol{\hat{y}} = \hat{\beta_0} + \hat{\beta_1} \boldsymbol{x}_1 + \boldsymbol{e}\]

Wir haben also eine erklärende Variable vergessen. Dies ist ein praktisch hochrelevantes Problem, denn häufig hat man relevante Variablen nicht auf dem Schirm oder es gibt zu uns relevant erscheinenden Variablen keine Daten.

Es stellt sich nun die Frage: was sind die Implikationen vergessener Variablen? Die Antwort ist recht unbequem, da wir hier nicht so glimpflich wie bisher davon kommen: im Falle vergessener Variablen ist Annahme A2 nicht mehr erfüllt und unser Schätzer \(\hat{\boldsymbol{\beta}}\) ist nun weder erwartungstreu noch konsistent - und zwar für alle unabhänigen Variablen in der Regression!

11.5.1 Folgen vergessener Variablen

Zunächst werden wir die Effekt von einer vergessenen Variable per Monte Carlo Simulation illustrieren. Zu diesem Zweck erzeugen wir Daten gemäß des Modells

\[\boldsymbol{y} = \beta_0 + \beta_1 \boldsymbol{x}_1 + \beta_2 \boldsymbol{x}_2 + \boldsymbol{\epsilon}\]

schätzen aber nur folgende Spezifikation:

\[\boldsymbol{\hat{y}} = \hat{\beta_0} + \hat{\beta_1} \boldsymbol{x}_1 + \boldsymbol{e}\] Das Ergebnis der Simulation ist in Abbildung 11.12 ersichtlich.

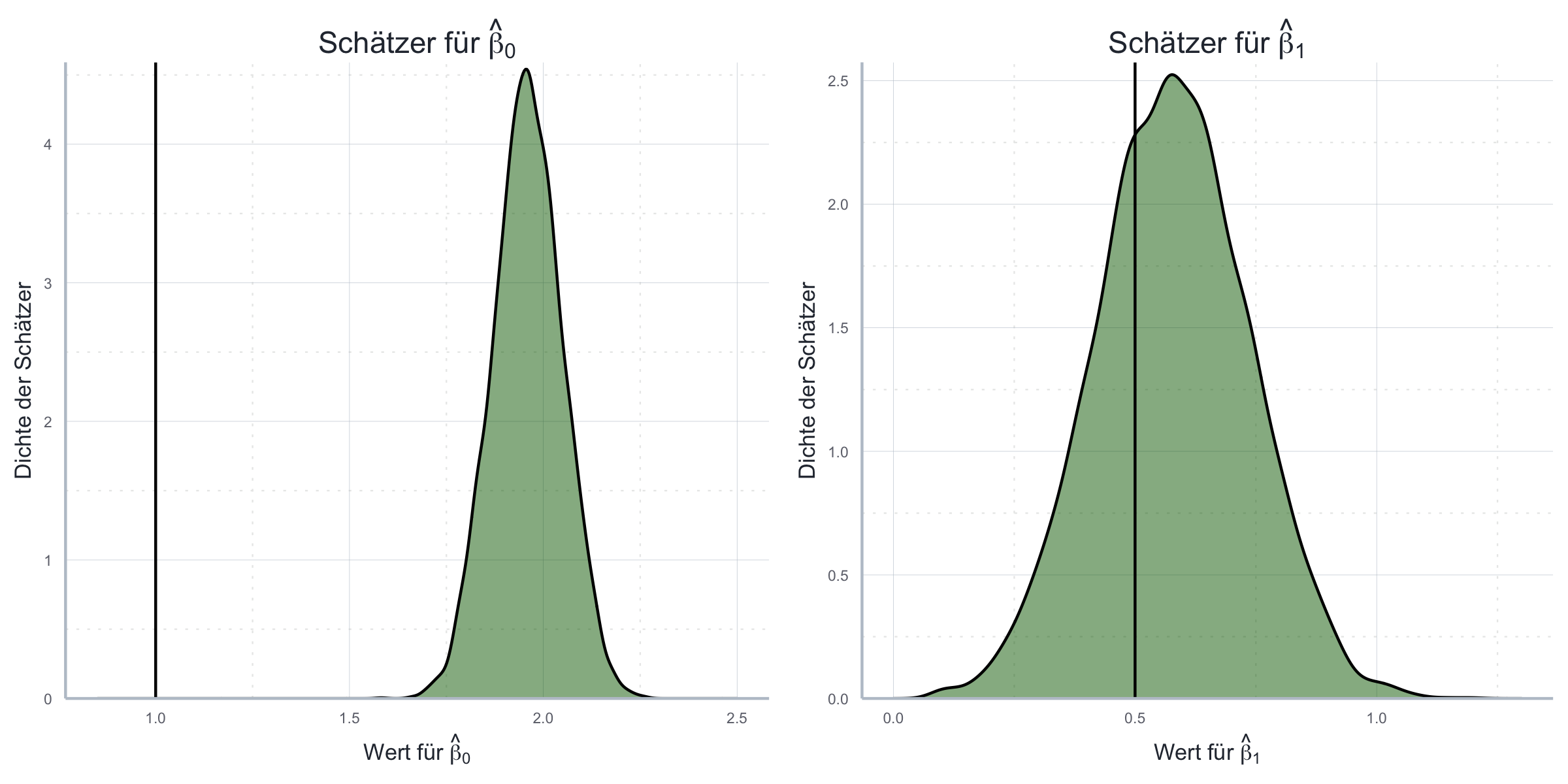
Abbildung 11.12: Folgen der vergessenen Variablen mit Bezug auf Erwartungstreue anhand von Monte Carlo Simulationen.

Wir sehen also, dass unsere OLS-Schätzer nun nicht mehr erwartungstreu sind! Dies können wir auch recht einfach analytisch zeigen. Nehmen wir generell an, das korrekte Modell sei gegeben durch:

\[\boldsymbol{y} = \boldsymbol{X\beta} + \boldsymbol{z}\gamma + \boldsymbol{\epsilon} \] wobei \(\boldsymbol{z}\) hier eine unabhängige Variable ist, die wir normalerweise in \(\boldsymbol{X}\) inkludiert hätten, hier zu Illustrationszwecken jedoch separat angeben um zu zeigen, was passiert wenn wir diese Variable vergessen. \(\gamma\) ist der zugehörige zu schätzende Parameter.

Wenn wir diese Gleichung nun schätzen ohne \(\boldsymbol{z}\) zu berücksichtigen bekommen wir folgenden Schätzer:

\[\boldsymbol{\hat{\beta}} = \left( \boldsymbol{X'X} \right)^{-1} \boldsymbol{X'y} = \boldsymbol{\beta} + \left( \boldsymbol{X'X} \right)^{-1} \boldsymbol{X'z\gamma} + \left( \boldsymbol{X'X} \right)^{-1} \boldsymbol{X'\epsilon}\]

Daraus resultiert, dass:

\[\mathbb{E}(\boldsymbol{\hat{\beta}} | \boldsymbol{X, z}) = \boldsymbol{\beta} + \left( \boldsymbol{X'X} \right)^{-1} \boldsymbol{X'z\gamma}\]

Das bedeutet, dass \(\boldsymbol{\hat{\beta}}\) nicht erwartungstreu ist, es sei denn (1) \(\boldsymbol{\gamma}=0\) oder (2) \(\boldsymbol{X'z}=0\). Fall (1) würde bedeuten, dass \(\boldsymbol{z}\) für die Analyse unserer abhängigen Variable gar nicht relevant wäre. Das würde bedeuten, wir hätten die Variable nicht ‘vergessen’, sondern zu Recht nicht inkludiert. Fall (2) würde bedeutetn, dass \(\boldsymbol{z}\) mit keiner der anderen erklärenden Variablen korreliert. Es ist sehr unwahrscheinlich, dass dies der Fall ist sollte \(\boldsymbol{z}\) tatsächlich relevant für die Erklärung von \(\boldsymbol{y}\) sein.

Das Vergessen relevanter Variablen führt also zu einer Korrelation der anderen unabhängigen Variablen mit dem Fehlerterm, da der Effekt von \(\boldsymbol{z}\) dann im Fehlerterm steckt und dieser dann mit den anderen unabhängigen Variablen korreliert. Zudem gilt, dass \(\mathbb{E}(\epsilon)\neq0\). Das alles geht mit einem Verlust der Erwartungstreue und auch der Konsistenz des Schätzers einher. Daher können wir die Verzerrung auch durch eine Vergößerung der Stichprobe nicht beheben.

11.5.2 Testen auf vergessene Variablen

Da wir den wahren datenerzeugenden Prozess nicht kennen ist es unmöglich direkt zu testen ob wir eine relevante Variable vergessen haben. Es gibt einen möglichen Test, der die Verwendung von Instrumentenvariablen einschließt - ein Thema, das wir später behandeln werden - allerdings basiert auch dieser Test dann wiederum auf nicht zu testenden Annahmen.

Insgesamt müssen wir uns hier also vor allem auf unsere theoretischen Überlegungen verlassen: wir müssen überlegen welche Variablen einen Einfluss auf unsere zu erklärende Variable haben könnten und diese Variablen müssen dann auf die eine oder andere Weise in der Regression berücksichtigt werden!

11.5.3 Reaktion auf vergessene Variablen

Das ist diesmal einfach: fügen Sie ‘einfach’ die relevanten Variablen zu Ihrer Regression hinzu. Wenn Sie dazu keine Daten haben hilft Ihnen allerhöchstens die Verwendung von Instrumentenvariablen.⁹⁵

11.6 Falsche funktionale Form

Eine zentrale Annahme des linearen Regressionsmodells ist die Linearität des datenerzeugenden Prozesses (A1). Wenn diese Annahme verletzt ist wäre unser Schätzer weder erwartungstreu noch konsistent.

Wir haben aber auch gelernt, dass die Annahme der Linearität sich nur auf die Parameter bezieht. Das bedeutet, dass bestimmte nicht-lineare Zusammenhänge durchaus mit OLS geschätzt werden können, wenn wir die Daten entsprechend transformieren. Dies geschieht durch die Wahl der funktionalen Form. Am besten wir illustrieren dies durch ein univariates Beispiel.

So ist auf den ersten Blick ersichtlich, dass der Zusammenhang zwischen BIP und Konsumausgaben direkt linear ist, siehe Abbildung 11.13.

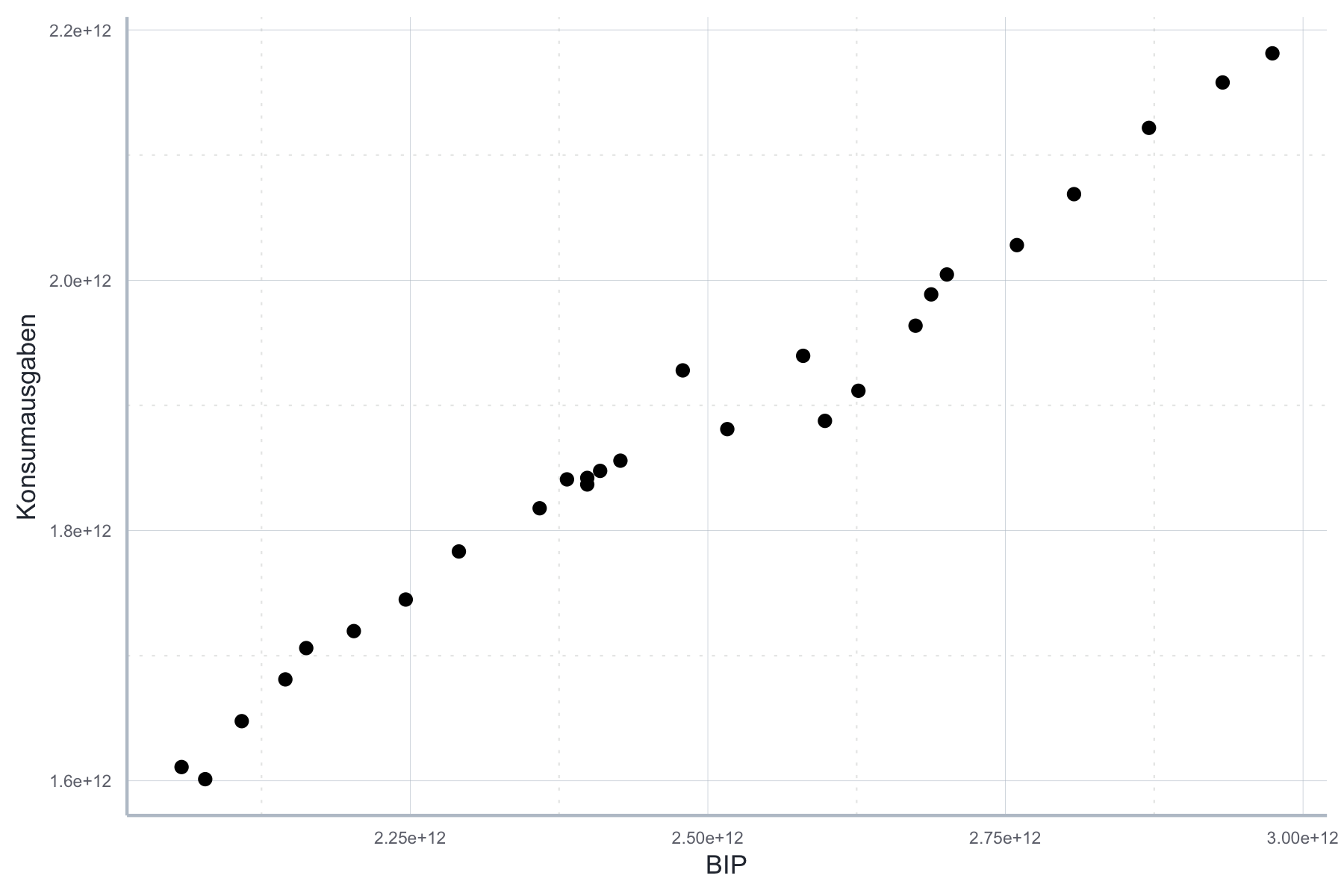
Abbildung 11.13: Linearer Zusammenhang zwischen BIP und Konsumausgaben.

Wir könnten den Zusammenhang also unmittelbar mit OLS schätzen ohne gegen Annahme A1 zu verstoßen.

Der Zusammenhang zwischen BIP pro Kopf und Kindersterblichkeit im Jahr 2000 erscheint dagegen nicht linear zu sein, siehe Abbildung 11.14.

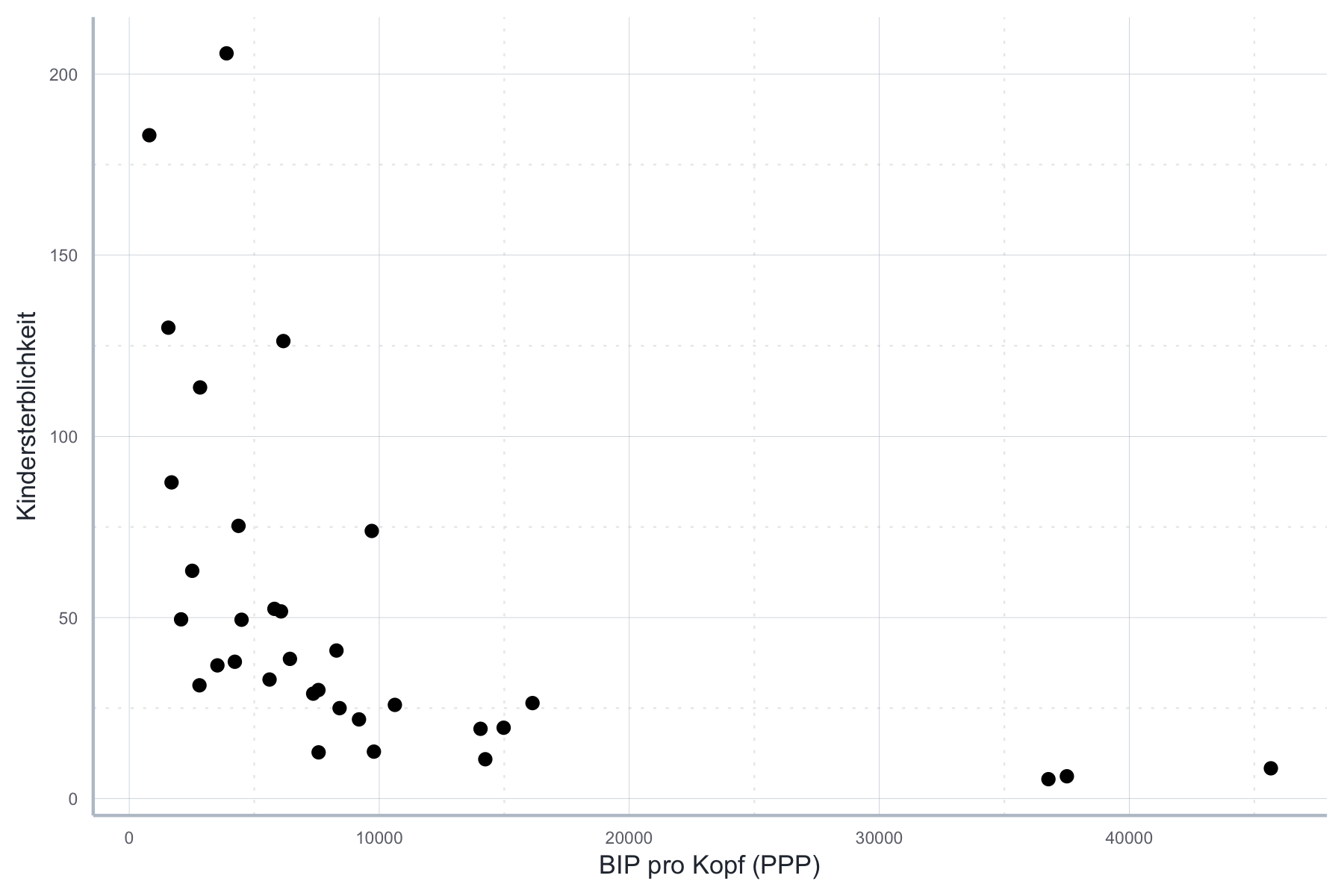
Abbildung 11.14: Nicht-linearer Zusammenhang zwischen BIP und Kindersterblichkeit.

Wenn wir diesen Zusammenhang mit OLS schätzen würden, würden wir klar gegen Annahme A1 verstoßen. Die Konsequenz wäre, dass unser Schätzer weder erwartungstreu, noch konsistent noch effizient wäre.

Gleichzeitig können wir durch die Wahl einer alternativen funktionalen Form den Zusammenhang linearisieren. Dazu nehmen wir einfach den Logarithmus, wie in Abbildung 11.15.

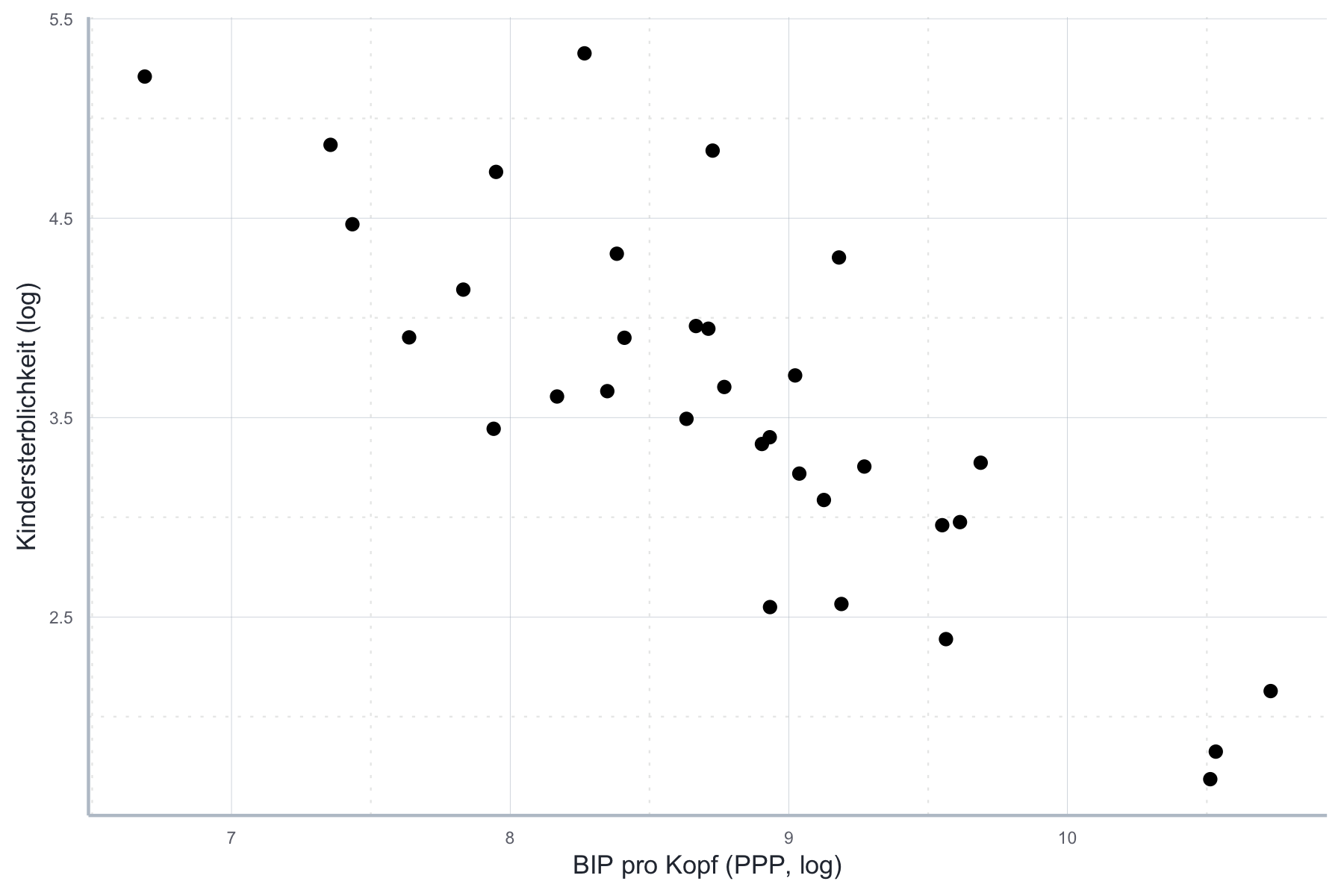
Abbildung 11.15: Logarithmierter Zusammenhang zwischen BIP und Kindersterblichkeit.

Diesen Zusammenhang können wir nun mit OLS schätzen ohne gegen A1 zu verstoßen! Das zeigt, dass die falsche Wahl der funktionalen Form, also die nicht korrekte Transformation der Variablen, große Implikationen für die Eigenschaften unserer Schätzer haben kann!

11.6.1 Folgen einer falschen funktionalen Form

Wie bereits erwähnt bezieht sich die Wahl der funktionalen Form direkt auf Annahme A1. Wie wir oben gesehen haben ist diese Annahme wichtig um die Konsistenz und Erwartungstreue des OLS-Schätzers herzuleiten. Mit anderen Worten: ist A1 nicht erfüllt, z.B. durch die Wahl einer falschen funktionalen Form, ist der OLS-Schätzer nicht mehr erwartungstreu und konsistent. Wir müssen also entweder die funktionale Form ändern oder ein anderes Schätzverfahren wählen.

11.6.2 Testen auf die richtige funktionale Form

Bei der Wahl der funktionalen Form spielen vor allem theoretische Überlegungen eine wichtige Rolle. Auch eine Inspektion der paarweisen Beziehungen zwischen abhängigen und unabhängigen Variablen ist hilfreich. Diese sollte immer am Anfang einer jeden empirischen Untersuchung stehen, um einen ersten Überblick über die Art der zu untersuchenden Zusammenhänge zu bekommen.

Wenn Sie ein Schätzung dann nach bestem Wissen durchgeführt haben, sollten Sie natürlich trotzdem abschließend überprüfen ob Sie die richtige funktionale Form ausgewählt haben. Eine wirksame Methode zur Überprüfung unserer funktionalen Form ist dabei die Inspektion des Tukey-Anscombe Plots. Haben wir die richtige Form gewählt werden wir hier keine Struktur erkennen können. Zeigen die Residuen jedoch eine klare Struktur auf ist das ein Signal, dass wir eine andere funktionale Form ausprobieren sollten. Das möchten wir zunächst anhand von folgendem Beispiel kurz illustrieren.

Anwendungsbeispiel: Durkheim und der Selbstmord in seinem Werk Der Selbstmord unterscheidet Emile Durkheim zwischen einem ‘anomischer Selbstmord’, der auf eine moralische Verwirrung, bzw. fehlende soziale Einbettung in modernen Gesellschaften zurückzuführen ist, und einem ‘fatalistischer Selbstmord’, der seine Ursache in der Erstickung individueller Bedürfnisse in archaischen Gesellschaften hat. Man könnte daraus die Hypothese ableiten, dass es entweder (1) einen U-förmigen Zusammenhang zwischen sozialer Kohäsion und der Wahrscheinlichkeit für einen Selbstmord gibt, oder aber, dass (2) es in mordernen Gesellschaften einen negativen, in archaischen Gesellschaften einen positiven Zusammenhang zwischen sozialer Kohäsion und der Wahrscheinlichkeit für einen Selbstmord gibt. Nehmen wir einmal an, das wäre tatsächlich so und wir hätten Daten zur sozialen Kohäsion und Selbstmordwahrscheinlichkeit gesammelt. Eine erste visuelle Inspektion der (hier simulierten) Daten in Abbildung 11.16 zeigt sofort, dass kein linearer Zusammenhang besteht und auch ein Logarithmieren der Daten nicht weiterhilft. Bereits an dieser Stelle sollten wir uns von einer einfachen linearen Spezifikation verabschieden. Gehen wir aber zu Illustrationszwecken davon aus, wir hätten dennoch das folgende lineares Modell geschätzt:

\[\begin{align} P_{\text{Suizid}} = \beta_0 + \beta_1 KOH + \epsilon \end{align}\]

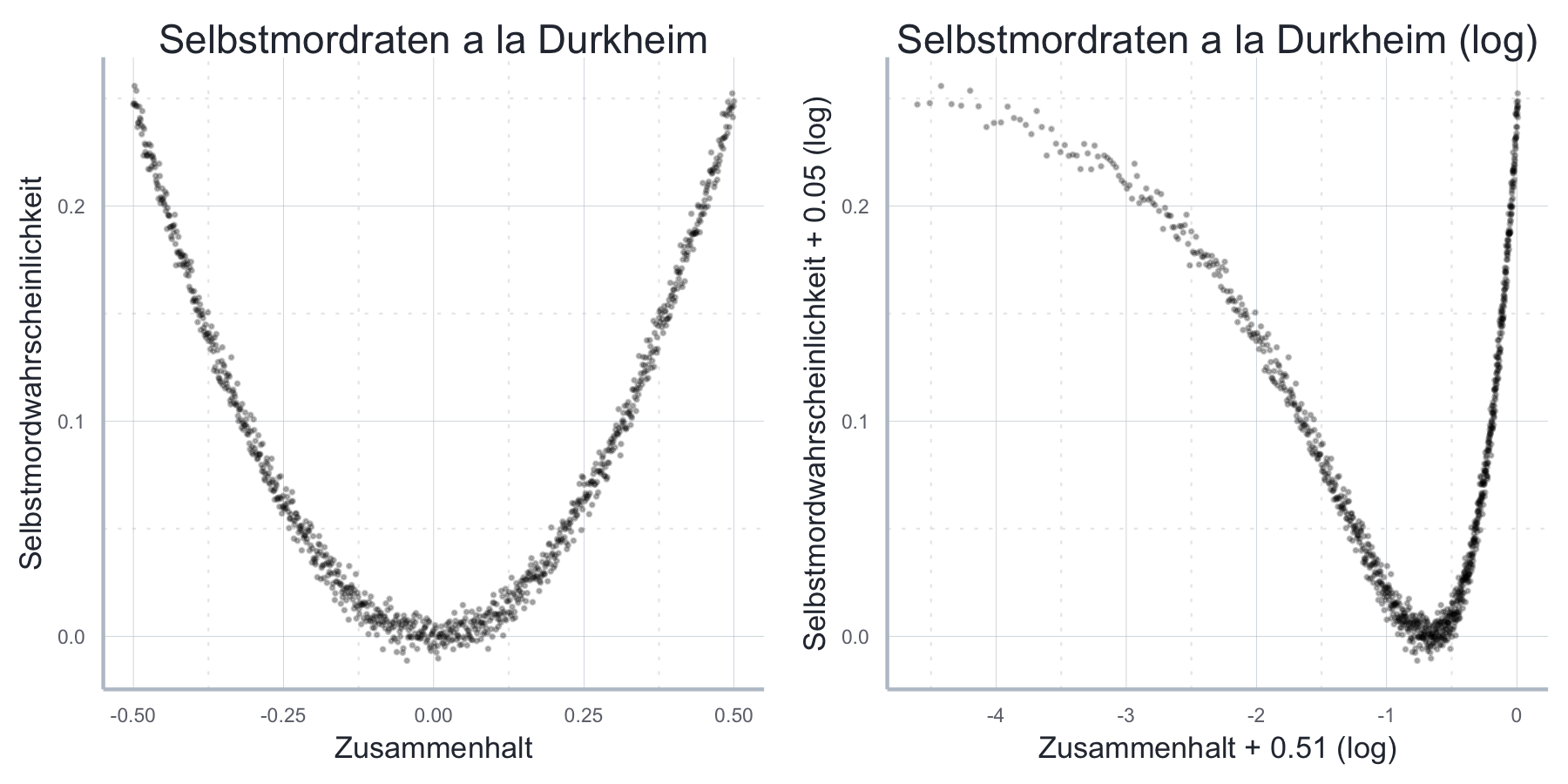
Abbildung 11.16: Simulierte Daten für Durkheim-Beispiel zum Zusammenhang zwischen sozialem Zusammenhalt und der Wahrscheinlichkeit zum Selbstmord.

In diesem Fall würde uns eine Inspektion der Schätzgerade in Abbildung 11.17a) oder aber des TK-Plots in Abbildung 11.17b) schnell vor Augen führen, dass die gewählte funktionale Form unpassend ist.

Abbildung 11.17: Die Schätzung eines linearen Modells auf die simulierten Durkheim-Daten ist eindeutig fehlspezifiziert.

Wenn wir der zweiten Interpretation oben folgen könnten wir in einem nächsten Schritt unsere Stichprobe aufteilen und überprüfen ob es in mordernen Gesellschaften einen negativen, in archaischen Gesellschaften einen positiven Zusammenhang zwischen sozialer Kohäsion und der Wahrscheinlichkeit für einen Selbstmord gibt. Wie in Abbildung 11.18 zu sehen, weisen die jeweiligen TA-Plots weiterhin eine klare Strukur auf, auch wenn der Fit des Modells insgesamt besser geworden ist.

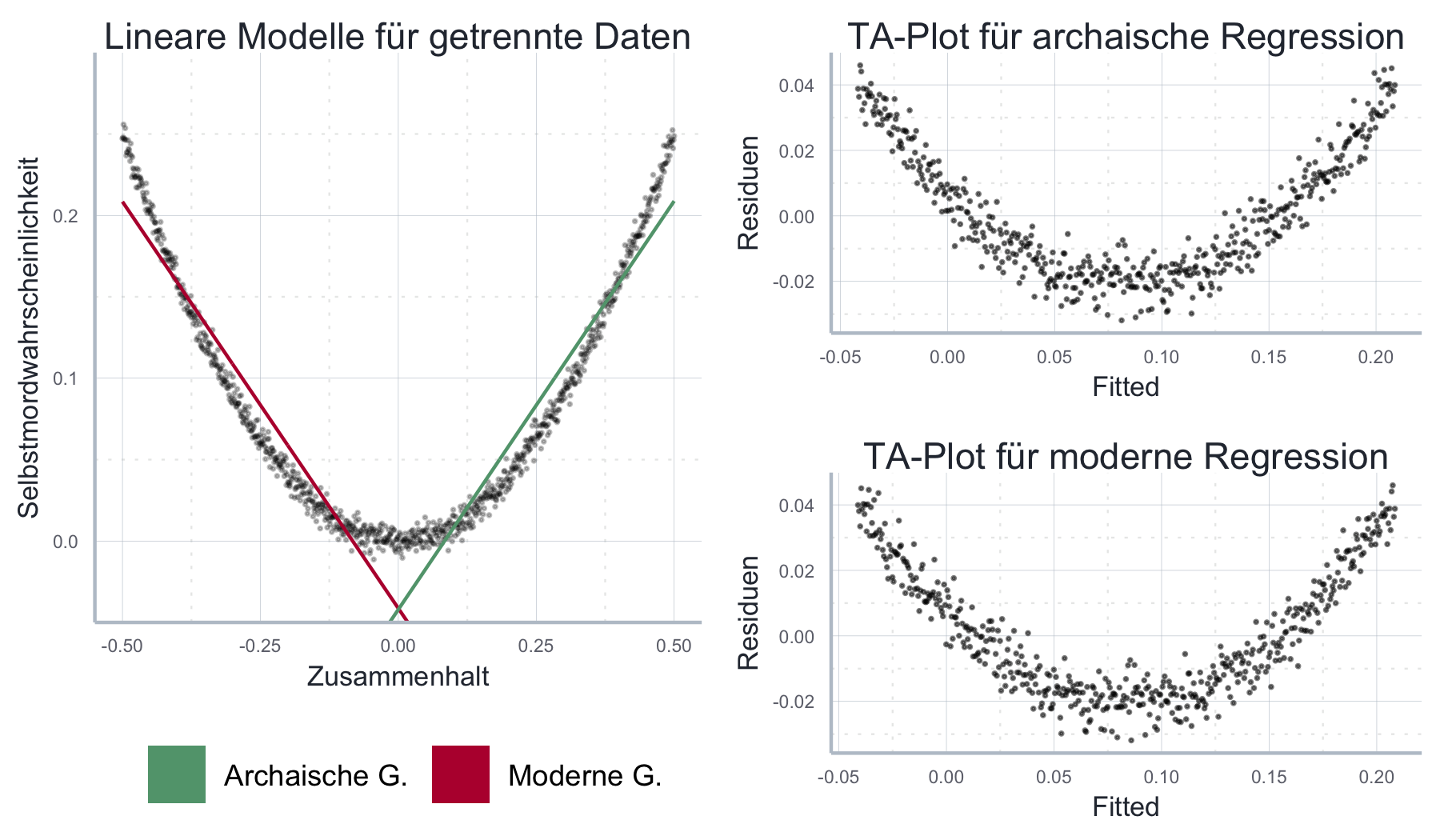
Abbildung 11.18: Auch eine Aufsplittung der Samples führt nicht dazu, dass der nicht-lineare Zusammenhang richtig geschätzt wird.

Im hier vorliegenden stilisierten Beispiel liegt der Grundfehler jedoch darin, dass wir bislang immer nur einen linearen Zusammenhang zwischen Kohäsion und Selbstmordwahrscheinlichkeit untersucht haben. Die Daten sind aber eindeutig nicht-linear. Wir können dieses Problem addressieren, indem wir einen quadratischen Term in unsere Schätzgleichung aufnehmen und folgendes Modell schätzen (das weiterhin linear in den Parametern \(\boldsymbol{\beta}\) ist):

\[\begin{align} P_{\text{Suizid}} = \beta_0 + \beta_1 KOH + \beta_2 KOH^2 + \epsilon \end{align}\]

Wie wir in Abbildung 11.19 sehen, ist das Modell nun deutlich besser spezifiziert und der TA Plot gibt keinen Hinweis auf einen Verstoß gegen die OLS-Annahmen. Der Preis den wir hier zahlen liegt in der nicht gerade intuitiven Interpretation des quadratischen Terms \(\beta_2\) in der Schätzgleichung oben. Es ist hier jedoch der einzige Weg, das Modell ohne Verstoß gegen A1 zu schätzen.

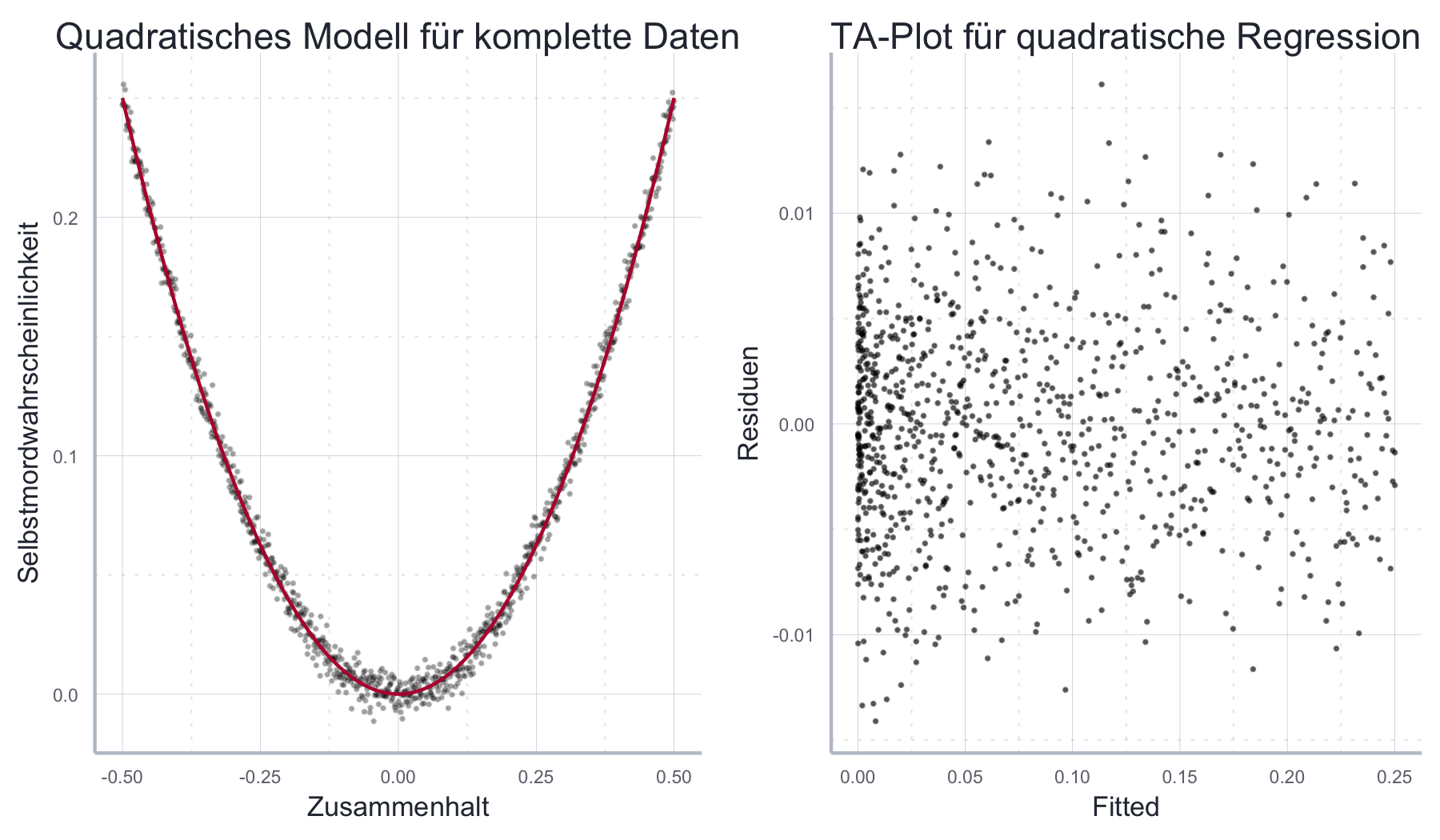
Abbildung 11.19: Durch das Hinzufügen eines quadratischen Terms in die Schätzgleichung kann das Modell korrekt spezifiziert und geschätzt werden.

Natürlich kann die Struktur der Residuen aber auch andere Gründe haben, z.B. Heteroskedastie oder Autokorrelation. Neben der Tatsache, dass die Struktur sich grafisch aber meist anders zeigt, haben Sie in den vorangegangenen Abschnitten ja auch statistische Tests für diese Probleme kennen gelernt, sodass Sie durch sukszessives Testen und Ausprobieren die möglichen Gründe für eine Misspezifikation und in der Folge eine angemessene funktionale Form identifizieren können. Tatsächlich ist es aber so, dass während die quantitativen Tests für Heteroskedastie und Autokorrelation recht weit verbreitet sind, ist für die Untersuchung der Linearitätsannahme der TK-Plot häufig absolut unverzichtbar. Aber natürlich gibt es auch einige Tests, die manchmal verwendet werden um die Wahl der funktionalen Form zu überprüfen. Der bekannteste Test ist dabei der so genannte RESET Test. RESET steht dabei für REgression Specification Error Test. Dieser Test wird mit der Funktion resettest() durchgeführt und testet die \(H_0\), dass wir die richtige funktionale Form gewählt haben.

Wir illustrieren den Test anhand folgenden Beispiels, in dem wir den uns bereits bekannten Datensatz zu Journaldaten analysieren.

Wir betrachten den Zusammenhang zwischen der Abonnentenanzahl und dem Preis pro Zitation. Wie wir in Abbildung 11.20 sehen ist dieser Zusammenhang alles andere linear:

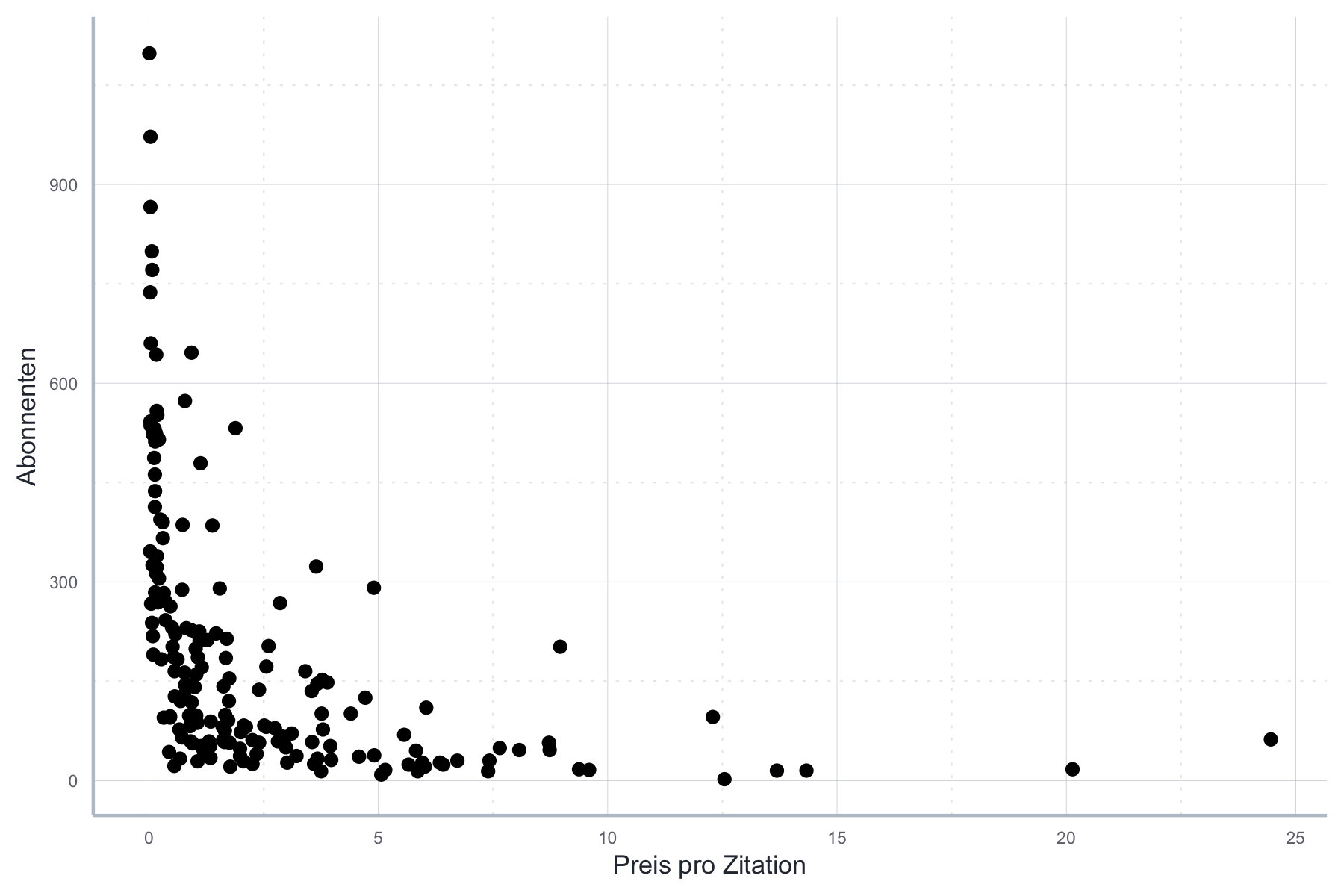
Abbildung 11.20: Nicht-linearer Zusammenhang zwischen Abonnenten und dem Preis pro Zitation

Für die folgende Spezifikation wäre der OLS-Schätzer also weder konsistent noch erwartungstreu, da hier ein klarer Verstoß gegen A1 vorliegen würde. Die folgende Schätzung ist entsprechend nicht zu gebrauchen:

\[\text{Abonnenten} = \beta_0 + \beta_1 \text{Zitationspreis} + \epsilon\]

lin_mod <- lm(Abonnenten~`Preis pro Zitation`, data=journal_daten)

Wenn wir aber beide Größen logarithmieren würden, wäre der Zusammenhang schon ziemlich linear, siehe Abbildung 11.21.

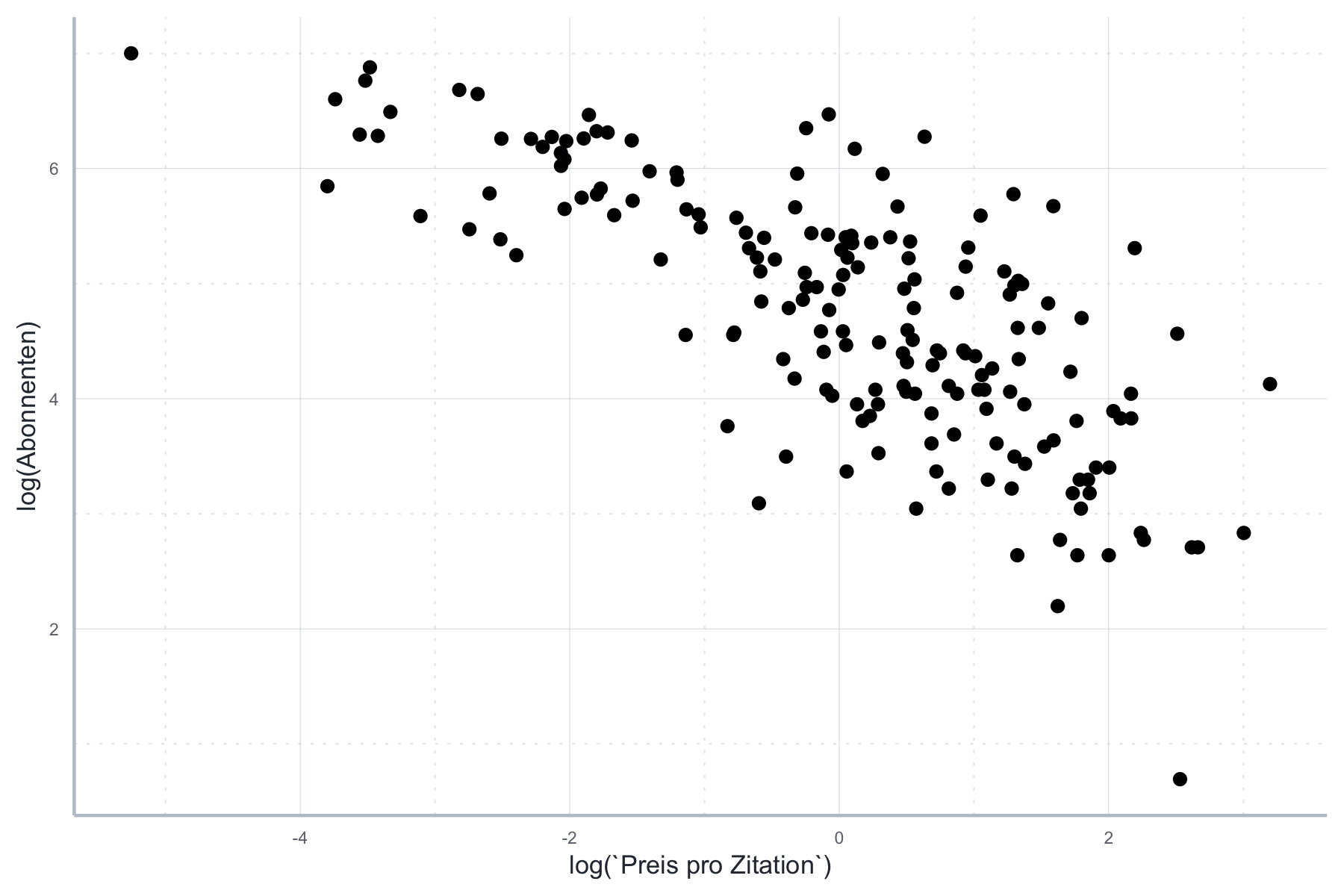
Abbildung 11.21: Logarithmierter Zusammenhang zwischen Abonnenten und Preis pro Zitation.

Die folgende Gleichung wäre also nicht unbedingt mit einem Verstoß gegen A1 verbunden:

\[\ln(\text{Abonnenten}) = \beta_0 + \beta_1 \ln(\text{Zitationspreis}) + \epsilon\]

log_mod <- lm(log(Abonnenten)~log(`Preis pro Zitation`), data=journal_daten)

Wir verwenden die Funktion resettest() um diese Intuition zu überprüfen. Zunächst testen wir auf eine Misspezifikation im linearen Modell, indem wir der Funktion resettest() das Schätzobjekt übergeben:

resettest(lin_mod)

#> 
#>  RESET test
#> 
#> data:  lin_mod
#> RESET = 28.99, df1 = 2, df2 = 176, p-value = 1.31e-11

Wenig überraschend müssen wir die \(H_0\) des korrekt spezifizierten Modells klar ablehnen. Wie sieht es mit dem Log-Lin Modell aus?

resettest(log_mod)

#> 
#>  RESET test
#> 
#> data:  log_mod
#> RESET = 1.4409, df1 = 2, df2 = 176, p-value = 0.2395

Hier kann \(H_0\) nicht abgelehnt werden, dementsprechend können wir nicht davon ausgehen, dass unser Modell misspezifiziert ist.

Beachten Sie aber, dass der RESET Test keine abschließende Sicherheit bieten kann. Hypothesentests bezüglich der funktionalen From sind nicht so zuverlässig wie z.B. die Tests auf Autokorrelation oder Heteroskedastie. Sie werden also immer wieder Situationen erleben in denen der RESET Test ein Modell ablehnt, das sie aufgrund empirischer und theoretischer Überlegungen gut verteidigen könnten und umgekehrt. Daher sollte er immer mit Theorie und Beobachtung kombiniert werden.

11.6.3 Wahl der funktionalen Form

Die Wahl der funktionalen Form hat nicht nur das Ziel Annahme 1 zu erfüllen. Da auch die Interpretation der geschätzten Koeffizienten je nach funktionaler Form eine andere ist, kann die Wahl einer bestimmten funktionalen Form auch theoretisch motiviert sein. Gerade die so genannten ‘log-log-Modelle’ sind häufig auch theoretisch sehr interessant, da wir hier Elastizitäten direkt schätzen können. Tabelle 11.1 gibt einen Überblick über häufig gewählte Spezifikationen und ihre Interpretation für das einfache lineare Regressionsmodell. Für das Modell mit mehreren unabhängigen Variablen ist die Interpretation äquivalent.

Tabelle 11.1: Spezifikationen der funktionalen Form und ihre Interpretationen.

Modellart	Schätzgleichung	Interpretation der Koeffizienten
Level-Level	\(y=\beta_0+\beta_1x_1+\epsilon\)	Ändert sich \(x_1\) um \(1\) ändert sich \(y\) um \(\beta_1\)
Log-Level	\(\ln(y)=\beta_0+\beta_1x_1+\epsilon\)	Ändert sich \(x_1\) um \(1\) ändert sich \(y\) c.p. um ca. \(100\cdot\beta_1\%\)
Level-Log	\(y=\beta_0+\beta_1\ln(x_1)+\epsilon\)	Ändert sich \(x_1\) um ca. \(1\%\) ändert sich \(y\) c.p. um ca. \(\beta_1 / 100\)
Log-Log	\(\ln(y)=\beta_0+\beta_1\ln(x_1)+\epsilon\)	Ändert sich \(x_1\) um ca. \(1\%\) ändert sich \(y\) c.p. um ca. \(\beta_1\%\)

Illustrieren wir die Wahl der funktionalen Form an folgendem Beispiel. Die Daten kommen von Epple und McCallum (2006) und enthalten Information zum Preis und zum Konsum von Hähnchenfleisch.

Wie in Abbildung 11.22 ersichtlich ist dieser Zusammenhang an sich nicht linear, kann aber durch Logarithmieren in eine lineare Form gebracht werden.

Abbildung 11.22: Nicht-linearer und logarithmierter Zusammenhang zwischen Preis und Konsum von Hühnchenpreis.

Die folgende Gleichung ist also konsistent mit A1 und kann entsprechend mit OLS geschätzt werden:

\[\ln(q) = \beta_0 + \beta_1 \ln(p) + \epsilon\]

log_model <- lm(log(q)~log(p), data = chicken_daten)

Diese Form ist dann linear und konsistent mit A1. Entsprechend macht es Sinn den Output zu interpretieren.

summary(log_model)

#> 
#> Call:
#> lm(formula = log(q) ~ log(p), data = chicken_daten)
#> 
#> Residuals:
#>       Min        1Q    Median        3Q       Max 
#> -0.228363 -0.080077 -0.007662  0.106041  0.218679 
#> 
#> Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)  3.71694    0.02236   166.2   <2e-16 ***
#> log(p)      -1.12136    0.04876   -23.0   <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 0.118 on 50 degrees of freedom
#> Multiple R-squared:  0.9136, Adjusted R-squared:  0.9119 
#> F-statistic:   529 on 1 and 50 DF,  p-value: < 2.2e-16

Wir würden den geschätzten Koeffizienten von \(\beta_1\) folgendermaßen interpretieren: wenn der Preis von Hühnerfleisch um \(1\%\) steigt wird der Konsum um ca. \(1.12\%\) zurückgehen.

11.7 Normalverteilung der Fehlerterme

Wie oben beschrieben ist die Annahme A5 für die besonders wichtigen Eigenschaften Erwartungstreue, Effizienz und Konsistenz nicht notwendig. Sie erleichtert aber Hypothesentests und wird häufig als Indiz für ein gut spezifiertes Modell gesehen.

Da wir die Fehlerterme nicht direkt beobachten können wird diese Annahme überprüft, indem die Verteilung der Residuen betrachtet wird. Damit eine visuelle Inspektion möglichst einfach ist verwenden wir hier einen so genannten Q-Q-Plot (siehe dazu Abbildung 11.23). Im Q-Q-Plot werden die tatsächlichen Quantile der Verteilung der Residuen auf der y-Achse gegen die hypothetischen Quantile einer Normalverteilung auf der x-Achse abgebildet.

Um einen Q-Q-Plot mit ggplot2 zu produzieren speichern Sie die Residuen Ihrer Schätzung in einem tibble und spezifizieren sie als Ästhetik sample. Dann verwenden Sie als geoms die Befehle ggplot2::stat_qq() für die Darstellung der Residuen und ggplot2::stat_qq_line() um die Gerade zur leichteren Interpretation zu ergänzen:

ggplot2::ggplot(
  data = tibble::tibble(
    Residuen=residuals_from_reg1
    ),
  mapping = aes(sample=Residuen)) + 
  ggplot2::stat_qq() + ggplot2::stat_qq_line() +
  theme_bw()

Abbildung 11.23: Q-Q-Plot zur Überprüfung der Residuen.

In Abbildung 11.23 sind zwei Q-Q-Plots abgebildet. Plot a) zeigt einen relativ idealtypischen Q-Q-Plot, bei dem wir guten Gewissens von einer Normalverteilung der Residuen ausgehen können: hier liegen die Punkte ziemlich exakt auf der Q-Q-Line. Bei Plot b) in Abbildung 11.23 ist das dagegen nicht der Fall, weswegen wir skeptisch bezüglich aller Ergebnisse sein sollten, die auf der Normalverteilungsannahme aufbauen, also insbesondere bei den Standardfehlern, \(p\)-Werten und den Konfidenzintervallen. In einem solchen Fall können Sie versuchen, über Transformationen Ihrer Daten eine Normalverteilung der Residuen herzustellen. Bleibt das erfolglos oder ergibt es im konkreten Anwendungsfall keinen Sinn sollten Sie die Unsicherheit Ihrer Schätzung nicht über die normalen Standardfehler messen, sondern sich Techniken wie dem Huber-Schätzer oder dem noch robusteren Bootstrap bedienen.

11.8 Weitere Fehlerquellen: Systematische Messfehler, Selbstselektion und Simulatanität

Annahme A2, Exogenität der unabhängigen Variablen, kann nur aufgrund von drei weiteren Gründen verletzt werden: aufgrund von Messfehlern, von Selbstselektion der Stichprobe und aufgrund von Simulatanität. Diese Fehlerquellen sind etwas anders geartet als die anderen hier besprochenen Probleme: hier liegt keine direkte Fehlspezifikation des Modells vor, sondern der Fehler geschieht entweder auf Ebene der Datenerhebung (Messfehler, Selbstselektion) oder ist dem zu untersuchenden Zusammenhang inhärent (Simulatanität). Insofern können wir nicht wirklich auf diese Fehler testen sondern müssen bei der Auswahl unserer Daten und der Formulierung unseres Modells diese Fehlerquellen in Betracht ziehen.

Im Folgenden wollen wir kurz darstellen wie diese drei Fehlerquellen zu einer Verletzung von A2 führen.

11.8.1 Messfehler

Falls wir unsere abhängige Variable nicht korrekt messen können hängen die Implikationen von der Art des Messfehlers ab. Nehmen wir dazu an, die korrekte abhängige Variable wäre \(y^*\). Wir verfügen aber nur über eine näherungsweise Messung, \(y'\). Wenn es sich um einen zufälligen und additiven Messfehler handelt, also \(y^*=y'+w\) und \(w\propto\mathcal{N}(0, \sigma^2)\), dann kann man zeigen, dass der OLS Schätzer weiterhin erwartungstreu ist und lediglich ein gewisses Maß an Effizienz einbüst, da:

\[y^* = \boldsymbol{x'\beta} + \boldsymbol{\epsilon}\]

\[y'= \boldsymbol{x'\beta} + \boldsymbol{\epsilon} + \boldsymbol{w}= \boldsymbol{x'\beta} + \boldsymbol{v}\] und \(\boldsymbol{v}\propto\mathcal{N}(0, \sigma^2_v)\), wobei \(\sigma^2_v>\sigma^2_{\epsilon}\).

Bei anderen Formen des Messfehlers, z.B. multiplikativen Messfehler, oder besonderen Verteilungen des Messfehlers können wir nichts sicher über die Implikationen des Messfehlers sagen.

Wird dagegen eine unabhängige Variable nicht richtig gemessen sind die Implikationen in der Regel mit Sicherheit problematischer. Nehmen wir an, dass \(\boldsymbol{x}^*\) die korrekte Variable und \(\boldsymbol{x}'\) die gemessene Variable ist. Betrachten wir dann die folgende Spezifikation:

\[\boldsymbol{y}=\beta_0 + \beta_1\boldsymbol{x}^* + \boldsymbol{\epsilon}\]

Wenn wieder wie oben gilt \(\boldsymbol{x}' = \boldsymbol{x}^* + \boldsymbol{w}\) und damit \(\boldsymbol{x}^* = \boldsymbol{x}' - \boldsymbol{w}\), dann haben wir:

\[\boldsymbol{y}=\beta_0 + \beta_1(\boldsymbol{x}' - \boldsymbol{w}) + \boldsymbol{\epsilon}\] \[\boldsymbol{y}=\beta_0 + \beta_1\boldsymbol{x}' + \boldsymbol{\epsilon} - \beta_1\boldsymbol{w}\] \[\boldsymbol{y}=\beta_0 + \beta_1\boldsymbol{x}' + \boldsymbol{v}\]

In diesem Fall ist aber \(Cov(\boldsymbol{x'}, \boldsymbol{v})\neq0\) und Annahme A2 somit verletzt! Im Falle der multiplen Regression wären dabei die Schätzer für alle unabhängigen Variablen verzerrt - nicht nur die der falsch geschätzten Variable!

11.8.2 Selbstselektion

Eine Verzerrung tritt immer dann auf wenn bei der Erhebung der Stichprobe Beobachtungen mit bestimmten Werten einer unabhängigen Variablen mit größerer Wahrscheinlichkeit Eingang in die Stichprobe finden als andere. Dies ist besonders bei Umfragestudien eine große Gefahr. So sind in der Regel reiche Menschen weniger willig bei einer Vermögensumfrage zu antworten. Das klassische Beispiel kommt aus der Soziologie: Sie möchten über eine Umfrage die Determinanten für Lesekompetenz erfragen und schicken dazu das Material per Post an die möglichen Studienteilnehmer*innen. Wahrscheinlich werden Personen mit schlechten oder gar keinen Lesekompetenzen eher nicht antworten - Ihre Stichprobe wäre also verzerrt!

Heckman (1979) hat gezeigt, dass die Selbstselektion die gleichen technischen Konsequenzen hat wie eine vergessene Variable. Entsprechend werden wir die Herleitung hier nicht wiederholen.

11.8.3 Simulatanität

Wir sprechen von Simulatanität wenn ein beidseitiges kausales Verhältnis zwischen der abhängigen Variable und einer unabhängigen Variable herrscht.

Betrachten wir dazu folgenden einfaches Beispiel. Die Variablen \(Y\) und \(X\) werden in der Population folgendermaßen bestimmt:

\[\begin{align} Y&=\beta_0 + \beta_1 X + u\nonumber\\ X&=\alpha_0 + \alpha_1 Y + v\nonumber \end{align}\]

Wenn wir die Werte jeweils in die andere Gleichung einsetzen erhalten wir:

\[\begin{align} Y&=\frac{\beta_0+\beta_1\alpha_0}{1-\alpha_1\beta_1} + \frac{\beta_1v+u}{1-\alpha_1\beta_1}\nonumber\\ X&=\frac{\alpha_0+\alpha_1\beta_0}{1-\alpha_1\beta_1} + \frac{v+\alpha_1u}{1-\alpha_1\beta_1}\nonumber \end{align}\]

Wenn wir in einem solchen Fall die Gleichung für \(Y\) schätzen ergibt sich für \(Cov(X, u)=Cov(\frac{v+\alpha_1u}{1-\alpha_1\beta_1}, u)\neq 0\) und damit wiederum ein Verstoß gegen A2!

11.9 Anhang: Übersicht über die Testverfahren

Tabelle 11.2 bietet einen Überblick über die verschiedenen möglichen Probleme bei OLS Schätzungen, die Tests zur Prüfung dieser Probleme, der Implikationen sowie möglicher Lösungsansätze.

Tabelle 11.2: Übersicht über die Testverfahren.

Problem	Mögliche Tests	Implikationen	Reaktion
Heteroskedastie	Tukey-Anscombe Plot, Breusch-Pagan (bptest()), Goldfeld-Quandt (gqtest)	Reduzierte Effizienz, falsche Standardfehler	Robuste Standardfehler
Autokorrelation	Tukey-Anscombe Plot, Box–Pierce/Ljung–Box (Box.test), Durbin-Watson (dwtest), Breusch-Godfrey (bgtest())	Reduzierte Effizienz, falsche Standardfehler	Robuste Standardfehler
Multikollinearität	Hilfsregressionen	Größere Standardfehler	Ggf. alternative unabh. Variablen verwenden
Falsche funktionale Form	Theorie, RESET-Test, Tukey-Anscombe Plot	Verzerrter und ineffizienter Schätzer	Funktionale Form anpassen
Vergessene Variablen	Theorie, Tukey-Anscombe Plot	Verzerrter und ineffizienter Schätzer	Variablen ergänzen

11.10 Anhang: Relevante Theoreme und ihre mathematischen Beweise

An dieser Stelle werden alle relevanten Theoreme gesammelt. Während wir im Hauptteil des Kapitels die Implikationen der Theoreme anhand von Monte Carlo Simulationen illustriert haben finden Sie hier die dazugehörigen mathematischen Beweise.

11.10.1 Theoreme

Bei \(\sigma^2\) aus Gleichung in Theorem handelt es sich um einen unbekannten Parameter der Population, also Teil des DGP, den wir so nicht direkt beobachten k"onnen. Wir m"ussen diesen Parameter also "uber die Stichprobe sch"atzen. Daf"ur ben"otigen wir einen entsprechenden Sch"atzer (siehe Theorem ).

11.10.2 Beweise

---

91. Das ist insofern auch logisch, da wir ja einfach eine neue Variable \(z=x_2^2\) erstellen und diese dann als unabhängige Variable in der Regression verwenden könnten. Dann würde noch nicht einmal der Anschein der Nichtlinearität erweckt obwohl die Werte der unabhängigen Variablen die gleichen wären.↩︎

92. Wen der Beweis interessiert wird in Greene (2018) fündig.↩︎

93. Eigentlich ist \(\plim\) noch allgemeiner definiert, für die Anwendungen in der Ökonometrie ist diese Definition aber ausreichend. Wundern Sie sich aber nicht, wenn Sie in manchen mathematischen Texten leicht andere Definitionen finden.↩︎

94. Die mathematischen Grundlagen behandeln wir hier nicht, sie werden aber in der weiterführenden Literatur erläutert, z.B. in Kapitel 4 von Greene (2018).↩︎

95. Für eine genauere Einführung in Instrumentenvariablen siehe z.B. Greene (2018).↩︎