Chapter 10 Lineare statistische Modelle in R
Zentrales Lernziel dieses Kapitels ist der Umgang mit einfachen linearen Regressionsmodellen in R. Dabei werden die Inhalte der Kapitel zu Wahrscheinlichkeitstheorie sowie deskriptiver und schließender Statistik als bekannt vorausgesetzt (Kapitel 7, 8 und 9). Schauen Sie als erstes in diesen Kapitel nach wenn Sie ein hier verwendetes Konzept nicht verstehen und konsultieren Sie ansonsten ein Statistiklehrbuch (und freundliche Kommiliton*innen) Ihrer Wahl.
Verwendete Pakete
library(here)
library(tidyverse)
library(data.table)
library(latex2exp)
library(icaeDesign)
library(ggpubr)10.1 Einführung in die lineare Regression
Ziel linearer Regressionsmodelle ist es, ausgehend von einem Datensatz ein lineares Modell zu schätzen. Ein solches lineares Modell hat in der Regel die Form
\[Y_i = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_n x_n + \epsilon_i\] und soll uns helfen den linearen Zusammenhang zwischen den Variablen in \(x_i\) und \(Y_i\) zu verstehen. Dazu müssen wir die Parameter \(\beta_i\) schätzen, denn \(\beta_i\) gibt uns Informationen über den Zusammenhang zwischen \(x_i\) und \(Y_i\).
Sobald wir konkrete Werte für \(\beta_i\) geschätzt haben, können wir im Optimalfall von unseren Daten auf eine größere Population schließen und Vorhersagen für zukünftiges Verhalten des untersuchten Systems treffen. Damit das funktioniert, müssen jedoch einige Annahmen erfüllt sein, und in diesem Kapitel geht es nicht nur darum, die geschätzten Werte \(\hat{\beta}_i\) zu identifizieren, sondern auch die der Regression zugrundeliegenden Annahmen zu überprüfen.
Bevor wir uns Schritt für Schritt mit der Regression auseinandersetzen, wollen wir uns noch ein konkretes Beispiel anschauen.
10.1.1 Einführungsbeispiel
Beispiel: Konsum und Nationaleinkommen Wir sind daran interessiert wie zusätzliches Einkommen auf die Konsumausgaben in einer Volkswirtschaft auswirken.81 Daher stellen wir folgendes Modell auf:
\[C_i = \beta_0 + \beta_1 Y_i + \epsilon_i\]
wobei \(C_i\) für die Konsumausgaben und \(Y_i\) für das BIP steht. Diese Gleichung stellt unser statistisches Modell dar. Es hat zwei Parameter, \(\beta_0\) und \(\beta_1\), die wir mit Hilfe unserer Daten schätzen möchten. Wir laden uns also Daten zum Haushaltseinkommen und zum BIP aus dem Internet herunter und inspizieren die Daten zunächst visuell:
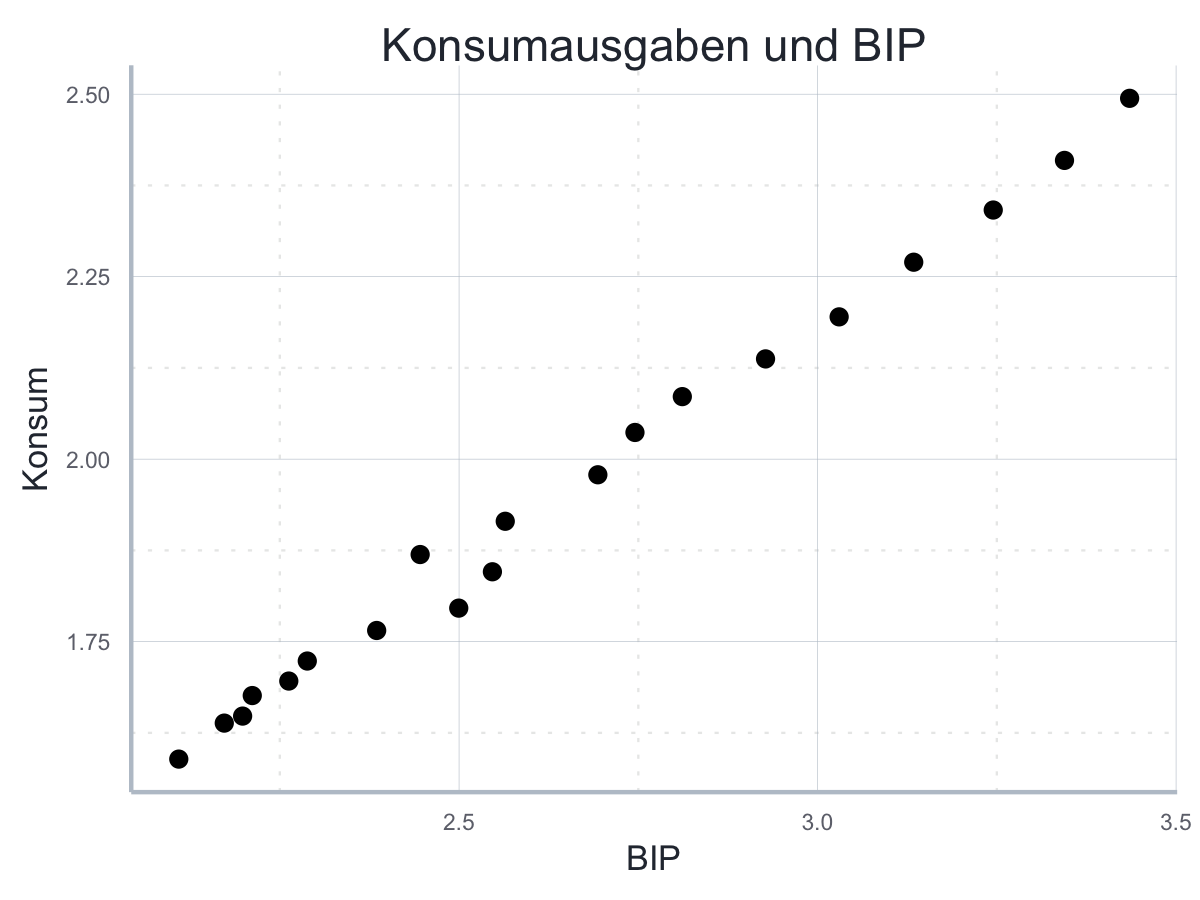
Der Zusammenhang scheint gut zu unserem linearen Modell oben zu passen, sodass wir das Modell mit Hilfe der Daten schätzen um konkrete Werte für \(\beta_0\) und \(\beta_1\) zu identifizieren:
#>
#> Call:
#> lm(formula = Konsum ~ BIP, data = bip_daten)
#>
#> Coefficients:
#> (Intercept) BIP
#> 0.1902 0.6655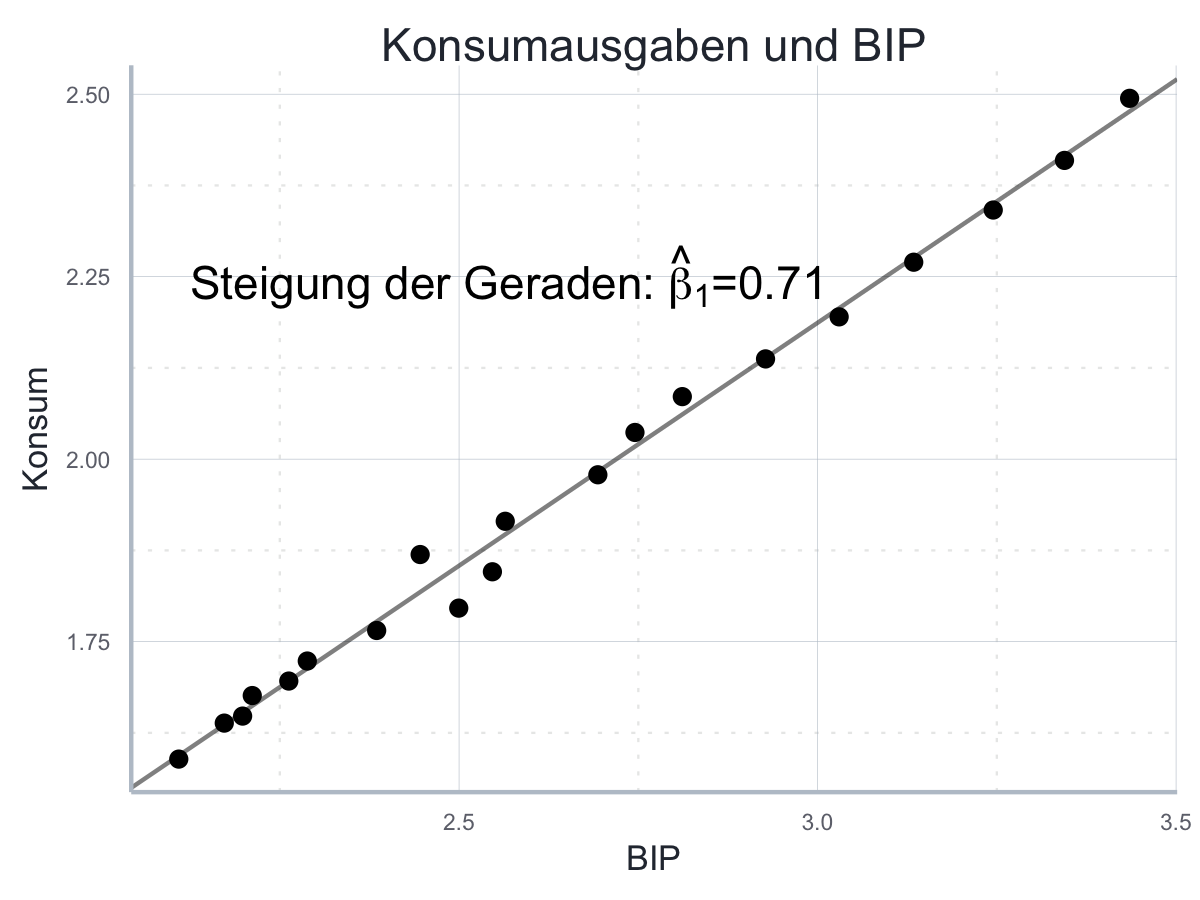
In dieser Abbildung korrespondiert \(\beta_0\) zum Achensabschnitt und \(\beta_1\) zur Steigung der Konsumgerade. Wir können \(\beta_0\) als die Konsumausgaben interpretieren, wenn das BIP Null betragen würde, und \(\beta_1\) als die marginale Konsumquote, also den Betrag, um den die Konsumausgaben steigen, wenn das BIP um einen Euro steigt. Die geschätzten Werte für \(\beta_0\) und \(\beta_1\) sind hier \(-184\) und \(0.7\). Auf dieser Basis können wir auch ausrechnen, wie hoch die Konsumausgaben in einer Volkswirtschaft mit einem BIP von 8000 wäre, indem wir uns einfach an der geschätzten Gerade bis zu diesem Betrag fortbewegen.
beta_0 <- schaetzung_bip[["coefficients"]][1]
beta_1 <- schaetzung_bip[["coefficients"]][2]
unname(beta_0 + beta_1*8000)#> [1] 5324.363Im aktuellen Beispiel wären das also
r round(unname(beta_0 + beta_1*8000), 2)Euro.
10.1.2 Überblick über die Inhalte des Kapitels
Im Folgenden werden wir uns zunächst mit den formalen Grundlagen der linearen Einfachregression, also der Regression mit einer \(x\)-Variable, und ihrer Implementierung in R beschäftigen. Insbesondere wird die Methode der kleinsten Quadrate (OLS) und die dafür notwendigen Annahmen eingeführt.
Danach werden wir typische Kennzahlen einer Regression diskutieren und lernen, wie wir die Güte einer Regression beurteilen können. Dieser Abschnitt enthält Auführungen zum \(R^2\), Standardfehlern von Schätzern, Konfidenzintervallen. Vieles ist eine Anwendung der in Kapitel 9 beschriebenen Konzepte zu schließender Statistik.
Nachdem wir den Ablauf einer Regressionsanalyse kurz zusammengefasst haben, generalisieren wir das Gelernte noch für den multiplen Fall, also den Fall wenn wir mehr als eine \(x\)-Variable in unserem Modell verwenden.
10.2 Grundlagen der einfachen linearen Regression
10.2.1 Grundlegende Begriffe
Wir betrachten zunächst den Fall der einfachen linearen Regression, das heißt wir untersuchen den Zusammenhang zwischen zwei Variablen, sodass unser theoretisches Modell folgendermaßen aussieht:
\[Y_i = \beta_0 + \beta_1 x_i + \epsilon_i\]
Alles was auf der linken Seite vom = steht bezeichnen wir als die LHS
(engl. left hand side), alles auf der rechten Seite als RHS
(engl. right hand side).
Wir bezeichnen \(Y_i\) als die abhängige Variable (auch: Zielvariable oder erklärte Variable). Das ist die Variable, die wir typischerweise erklären wollen. Im Eingangbeispiel waren das die Konsumausgaben.
Wir bezeichnen \(x_i\) als die unabhängige Variable (auch: erklärende Variable). Das ist die Variable, mit der wir die abhängige Variable erklären wollen. Im Eingangsbeispiel war das das BIP, denn wir wollten über das BIP erklären wie viel Geld in einem Land für Konsum ausgegeben wird.
Dabei ist nicht davon auszugehen, dass unser Modell den Zusammenhang zwischen den betrachteten Größen vollständig korrekt beschreibt - wie immer bei Modellen werden bestimmte Aspekte des untersuchten Systems nicht explizit berücksichtigt und unsere Fähigkeit, dass System in einem (hier sogar nur linearen) Modell abzubilden, ist unvollkommen. Um der Tatsäche Rechnung zu tragen, dass der Zusammenhang zwischen \(x_i\) und \(Y_i\) nicht exakt ist, führen wir auf der rechten Seite der Gleichung noch die Fehlerterme \(\epsilon_i\) ein.
Wir müssen für unser Modell annehmen, dass die Fehlerterme nur einen nicht-systematischen Effekt auf \(Y_i\) haben, ansonsten müssten wir sie explizit in unser Modell als erklärende Variable aufnehmen (dazu später mehr). Sie absorbieren quasi alle Einflüsse auf \(Y_i\), die nicht über \(x_i\) wirken. Damit wir die Funktion richtig schätzen können nehmen wir für die Fehler ein bestimmtes Wahrscheinlichkeitsmodell an. In der Regel nimmt man an, die Fehler seien i.i.d. (identically and independently distributed)82 normalverteilt mit Erwartungswert 0: \(\epsilon_i \ i.i.d. \propto \mathcal{N}(0, \sigma^2)\).
Nun ergibt auch die Groß- und Kleinschreibung in der Gleichung mehr Sinn: die \(x_i\) nehmen wir als beobachtete Größen hin und behandeln sie nicht als Zufallsvariablen (ZV).83 Die \(\epsilon_i\) sind als ZV definiert und da wir \(Y_i\) als eine Funktion von \(x_i\) und \(\epsilon_i\) interpretieren sind die \(Y_i\) auch ZV - und dementsprechend groß geschrieben. Die Fehlerterme werden per Konvention nie groß geschrieben - wahrscheinlich weil sich das für Fehler nicht gehört. Wer es ganz genau nehmen würde, müsste sie aber auch groß schreiben, denn sie sind als ZV definiert und diese werden eigentlich groß geschrieben.
Die Annahme von \(\mathbb{E}(\epsilon_i)=0\), also die Annahme, dass der Erwartungswert für jeden Fehler gleich Null ist, ist neben der Annahme, dass wir einen linearen Zusammenhang modellieren zentral: wir gehen davon aus, dass unser Modell im Mittel stimmt. Unter dieser Annahme gibt es keine systematischen Abweichungen der \(Y_i\) von der über \(\beta_0\) und \(\beta_1\) definierten Regressionsgeraden. Das ist allerding nur der Fall, wenn bestimmte Annahmen erfüllt sind (dazu später mehr).
10.2.2 Schätzung mit der Kleinste-Quadrate-Methode
Nachdem wir unser Modell aufgestellt haben, möchten wir nun die Parameter \(\beta_0\) und \(\beta_1\) schätzen. Wir schätzen diese Werte, denn sie sind für uns nicht unmittelbar beobachtbar: Wir brauchen also einen Schätzer. Ein Schätzer ist eine Funktion, die uns für die Daten, die wir haben, den optimalen Wert für den gesuchten Parameter gibt.84 Wir suchen also nach den Werten für \(\beta_0\) und \(\beta_1\) sodass die resultierende Gerade möglichst nahe an allen \(Y_i\) Werten ist, wie in Abbildung 10.1 aufgezeigt.
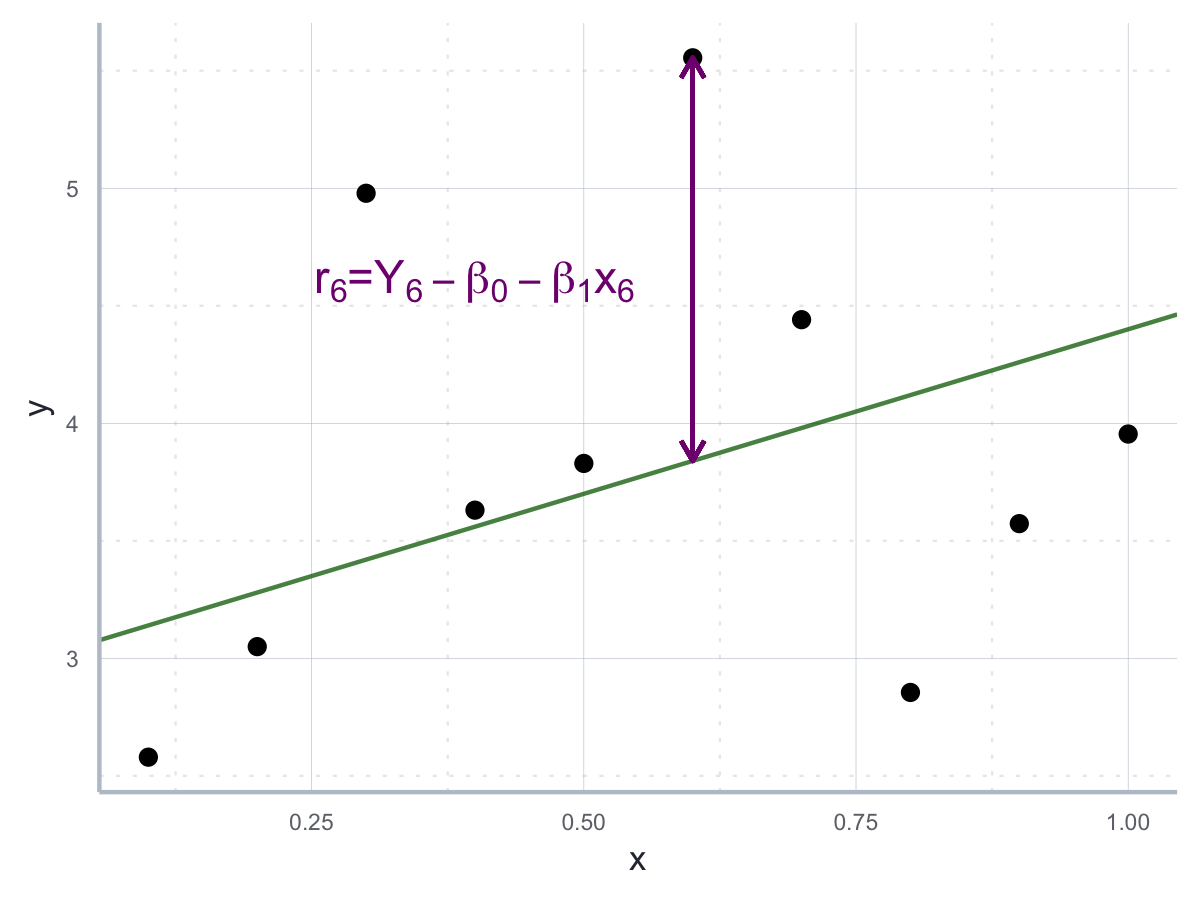
Abbildung 10.1: OLS Gerade als jene Gerade, welche den Abstand zu den quadrierten Residuen minimiert.
Wenn wir das händisch machen würden, könnten wir versuchen die Abstände zwischen den einzelnen \(Y_i\) und der Regressionsgerade zu messen und letztere so lange herumschieben, bis die Summe der Abstände möglichst klein ist. In gewisser Weise ist das genau das, was wir in der Praxis auch machen. Nur arbeiten wir nicht mit den Abständen als solchen, denn dann würden sich positive und negative Abstände ja ausgleichen. Daher quadrieren wir die Abstände, bevor wir sie summieren. Daher ist die gängigste Methode, Werte für \(\beta_0\) und \(\beta_1\) zu finden auch als Kleinste-Quadrate Methode (engl. ordinary least squares - OLS) bekannt.85 Die dadurch definierten Schätzer \(\hat{\beta}_0\) und \(\hat{\beta}_1\) sind entsprechend als OLS-Schätzer bekannt.
Wir bezeichnen die Abweichung von \(Y_i\) zu Regressionsgeraden als Residuum \(e_i\). Wie in der Abbildung zu sehen ist, gilt für die Abweichung von der Regressionsgeraden für die einzelnen \(Y_i\): \(e_i=(Y_i-\hat{\beta}_0-\hat{\beta}_1x_i)\). Wir suchen also nach den Werten für \(\hat{\beta}_0\) und \(\hat{\beta}_1\), für die die Summe aller Residuen minimal ist:
\[\hat{\beta}_0, \hat{\beta}_1 =\text{argmin}_{\beta_0, \beta_1} \sum_{i=1}^n(Y_i-\beta_0-\beta_1x_i)^2\]
Dabei bedeutet \(\text{argmin}_{\beta_0, \beta_1}\): wähle die Werte für \(\beta_0\) und \(\beta_1\), welche den nachfolgenden Ausdruck minimieren.
Diesen Ausdruck kann man analytisch so lange umformen bis gilt:86
\[\hat{\beta}_1 = \frac{\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{\sum_{i=1}^n(x_i-\bar{x})^2}\] und
\[\hat{\beta_0}=\bar{y}-\hat{\beta}_1\bar{x}\]
Zum Glück gibt es in R die Funktion lm(), welche diese Berechnungen für uns
übernimmt.
Wir wollen dennoch anhand eines Minimalbeispiels die Werte selber schätzen,
um unser Ergebnis dann später mit dem Ergebnis von lm() zu vergleichen.
Dazu betrachten wir folgenden (artifiziellen) Datensatz:
datensatz#> x y
#> 1 0.1 2.58
#> 2 0.2 3.05
#> 3 0.3 4.98
#> 4 0.4 3.63
#> 5 0.5 3.83Zuerst berechnen wir \(\hat{\beta}_1\):
\[\hat{\beta}_1 = \frac{\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{\sum_{i=1}^n(x_i-\bar{x})^2}\]
Dazu brauchen wir zunächst \(\bar{x}\), das ist in diesem Fall 0.3,
und \(\bar{y}\), in unserem Fall 3.614.
Dann können wir bereits rechnen:
\[\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})=(0.1-0.3)(2.58-3.614)+(0.2-0.3)(3.05-3.614)\\+(0.3-0.3)(4.98-3.614)+(0.4-0.3)(3.63-3.614)+(0.5-0.3)(3.83-3.614)=0.308\] und
\[\sum_{i=1}^n(x_i-\bar{x})^2=(0.1-0.3)^2+(0.2-0.3)^2+(0.3-0.3)^2+(0.4-0.3)^2+(0.5-0.3)^2=0.1\] Daher:
\[\hat{\beta_1}=\frac{0.308}{0.1}=3.08\]
Entsprechend ergibt sich für \(\hat{\beta}_0\):
\[\hat{\beta_0}=\bar{y}-\hat{\beta}_1\bar{x}=3.614-3.08\cdot 0.3=2.69\]
In R können wir für diese Rechnung wie gesagt die Funktion lm() verwenden.
In der Praxis sind für uns vor allem die folgenden zwei Argumente von lm()
relevant: formula und data.
Über data informieren wir lm über den Datensatz, der für die Schätzung
verwendet werden soll. Dieser Datensatz muss als data.frame oder
vergleichbares Objekt vorliegen.
Über formula teilen wir lm dann die zu schätzende Formel mit.
Die LHS und RHS werden dabei mit dem Symbol ~ abgegrenzt.
Wir können die Formel entweder direkt als y~x an lm() übergeben, oder wir
speichern sie vorher als character und verwenden die Funktion as.formula().
Entsprechend sind die folgenden beiden Befehle äquivalent:
lm(y~x, data = datensatz)
reg_formel <- as.formula("y~x")
lm(reg_formel, data = datensatz)Der Output von lm() ist eine Liste mit mehreren interessanten Informationen:
schaetzung <- lm(y~x, data = datensatz)
typeof(schaetzung)#> [1] "list"schaetzung#>
#> Call:
#> lm(formula = y ~ x, data = datensatz)
#>
#> Coefficients:
#> (Intercept) x
#> 2.69 3.08Die von lm() produzierte Liste enthält also die basalsten Informationen über
unsere Schätzung. Wir sehen unmittelbar, dass wir vorher richtig gerechnet haben,
da wir die gleichen Werte herausbekommen haben.
Wenn wir noch genauer wissen wollen, wie die Ergebnisliste aufgebaut ist,
können wir die Funktion str() verwenden:
str(schaetzung)Da die Liste aber tatsächlich sehr lang ist, wird dieser Code hier nicht ausgeführt. Es sei aber darauf hingewiesen, dass wir die geschätzen Werte auf folgende Art und Weise direkt ausgeben lassen können:
schaetzung[["coefficients"]]#> (Intercept) x
#> 2.69 3.08Dies ist in der Praxis häufig nützlich, z.B. wenn wir wie in der Einleitung Werte mit Hilfe unseres Modell vorhersagen wollen. Zum Abschluss sehen wir in Abbildung 10.2 die Daten mit der von uns gerade berechneten Regressionsgeraden.
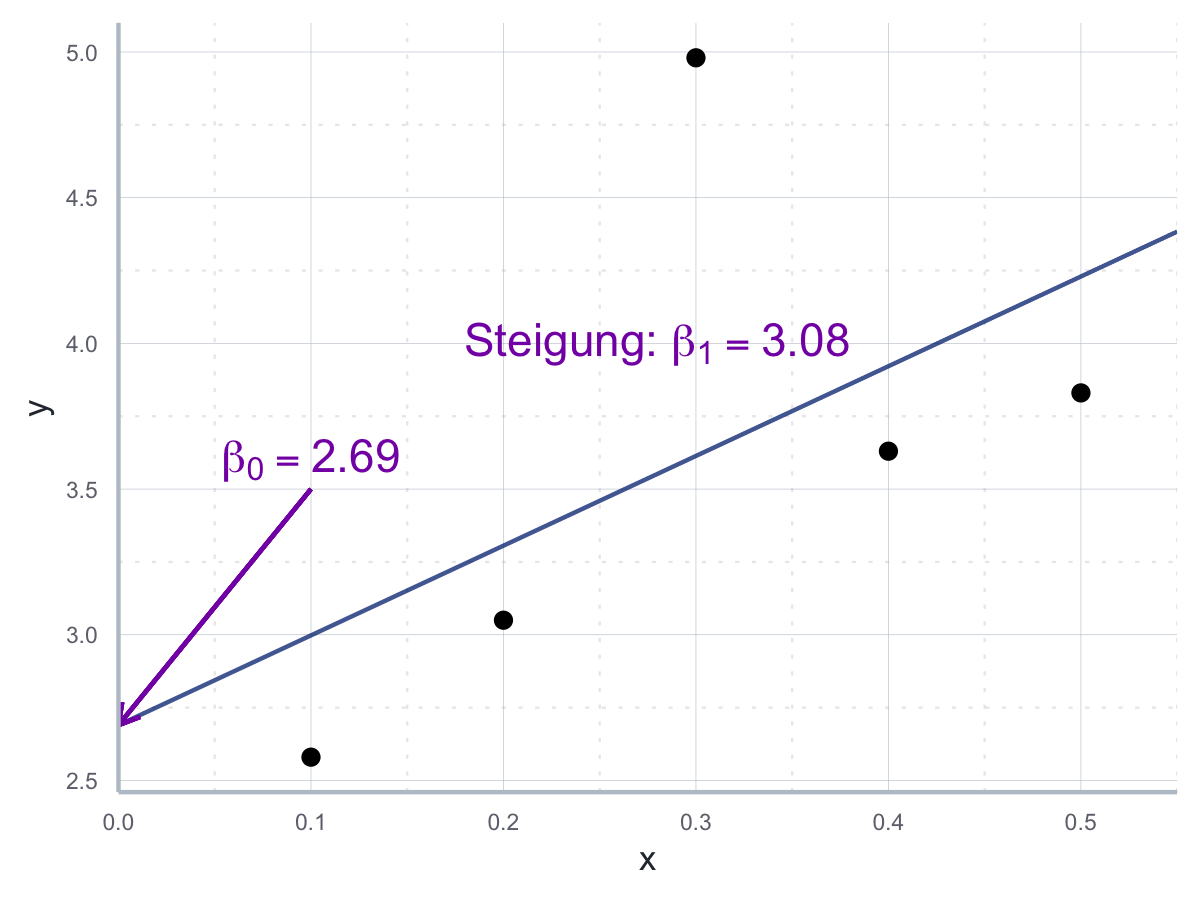
Abbildung 10.2: Regressionsgerade mit den berechneten Parameterwerten.
Zwar wissen wir jetzt, wie wir eine einfache lineare Regression schätzen, allerdings hört die Arbeit hier nicht auf! Unsere bisherige Tätigkeiten korrespondieren zu der in Kapitel 9 beschriebenen Parameterschätzung. Wir wollen aber auch noch die anderen beiden Verfahren, Hypothesentests und Konfidenzintervalle, abdecken und lernen, wie wir die Güte unserer Schätzung besser einschätzen können.
Zuvor wollen wir aber noch einmal genauer überprüfen, welche Annahmen genau erfüllt sein müssen, damit die OLS-Prozedur auch funktioniert.
10.2.3 Annahmen für den OLS Schätzer
Das lineare Regressionsmodell wird sehr häufig in der sozioökonomischen Forschung verwendet. Wie jedes statistische Modell basiert es jedoch auf bestimmten Annahmen, aus denen sich der sinnvolle Anwendungsbereich des Modells ergibt. Wann immer wir die lineare Regression verwenden sollten wir daher kritisch prüfen ob die entsprechenden Annahmen für den Anwendungsfall plausibel sind.
Um die Annahmen des linearen Regressionsmodell mathematisch wirklich exakt und hilfreich darzustellen müssen wir die Schätzer in Matrizenschreibweise formulieren. Das Arbeiten mit Matrizen wird in Kapitel 6 genauer eingeführt und das aktuelle Kapitel versucht ohne diese Konzepte auszukommen. Daher wollen wir an dieser Stelle noch in einer ‘lockeren’ verbalen Beschreibung der Annahmen verbleiben. Eine exakte Darstellung, die sich der Sprache der Matrizenalgebra bedient, sowie die genauen Methoden zum grafischen und statistischen Testen der Annahmen finden Sie dann in Kapitel 11.
Eine zentrale Annahme des linearen Modells ist, dass der Erwartungswert der Fehlerterme \(\epsilon\) gleich Null ist:
\[\mathbb{E}(\epsilon=0)\].
Diese Annahme setzt voraus, dass \(\epsilon\) keine Struktur hat und im Mittel gleich Null ist. Würden wir Informationen über eine Struktur in \(\epsilon\) haben, bedeutet das, dass wir eine weitere erklärende Variable in das Modell aufnehmen könnten, welche diese Struktur explizit macht. Wenn wir also eine wichtige Variable vergessen, dann ist diese Annahme verletzt und es kommt zu einem so genannten Omitted Variable Bias (siehe Kapitel 11). Genauso impliziert die Annahme auch, dass der Zusammenhang zwischen der erklärten und erklärenden Variablen auch tatsächlich linear ist. Wenn der Zusammenhang tatsächlich nichtlinear wäre, können wir nicht erwarten, dass unsere Fehler einen Erwartungswert von Null haben. In einem solchen Fall führt die Anwendung des OLS Schätzers zu irreführenden Ergebnissen.
Insgesamt kann man die Annahme vielleicht auch einfach so (sehr grob) zusammenfassen: wir nehmen an, dass wir unser Modell clever spezifiziert haben. Dabei ist wichtig zu beachten, dass wir hier eine Annahme über eine unbeobachtbare Größe der Population treffen, nämlich die Fehlerterme \(\epsilon\), und nicht über die Residuen \(e_i\) unserer Regression. Die Residuen \(e_i\) können wir beobachten, die echten Fehler \(\epsilon_i\) nicht. Entsprechend gibt es auch keinen abschließenden ‘Test’ dieser ersten Annahme.
Neben dieser zentralen ersten Annahme, nehmen wir des Weiteren an, dass es keinen systematischen Zusammenhang zwischen den Fehlern und den erklärenden Variablen gibt. Die Annahme wäre zum Beispiel verletzt, wenn für größere Werte von \(x\) die Messgenauigkeit drastisch in eine Richtung hin abnehmen würde. Auch bei dieser Annahme gilt, dass unsere Schätzer systematisch verzerrt werden sobald die Annahme nicht mehr erfüllt ist.
Zwei weitere Annahmen beziehen sich auf die Struktur der Fehlerterme: zu einen nehmen wir an, dass die Varianz der Fehlerterme konstant ist (‘Homoskedastizität’): \(Var(\epsilon_i)=\sigma^2\forall i\). Zum anderen nehmen wir an, dass die Fehler nicht untereinander korreliert sind: \(Cov(\epsilon_i, \epsilon_j)=0 \forall i,j\). Letzteres kann vor allem ein Problem sein, wenn die gleichen erklärenden Variablen zu unterschiedlichen Zeitpunkten gemessen werden. Bei diesen beiden Annahmen führt eine Verletzung zum Glück nicht mehr dazu, dass unser Schätzer systematisch verzerrt ist - er wird aber deutlich ungenauer.87
Gleiches gilt auch für die Annahme, dass keine der erklärenden Variablen eine lineare Transformation einer anderen erklärenden Variable ist, also \(\nexists a,b: x_i= q+b\cdot x_j \forall i,j\). Praktisch tritt dieser Fall, den man auch als ‘perfekte Multikollinearität’ bezeichnet, nur selten auf. Würde tatsächlich perfekte Multikollinearität herrschen, wäre \(\hat{\beta}\) schlicht nicht definiert. Praktisch relevant wird die Annahme allerdings deswegen, weil schon eine starke Korrelation zwischen den erklärenden Variablen die Schätzung deutlich ungenauer macht. Als generellen take-away können wir im Bezug auf diese Annahme als mitnehmen, dass wir in den erklärenden Variablen möglichst wenig Redundanz haben sollten.
Sind alle diese Annahmen erfüllt, dann gilt das so genannte Gauss-Markov-Theorem (GMT). Dieses Theorem ist ein wichtiger Grund für die Popularität der OLS-Methode: nach dem GMT ist der OLS-Schätzer für lineare Modelle der beste erwartungstreue Schätzer, den wir finden können. Oder cooler ausgedrückt: OLS ist der BLUE - der Best Linear Unbiased Estimator.
Mit “erwartungsteu” ist dabei gemeint, dass die Schätzer bei vielen Schätzversuchen im Mittel den wahren Wert \(\beta_i\) treffen, also der Erwartungswert jedes Schätzers \(\hat{\beta}_i\) der wahre Werte \(\beta\) ist. Mit “der beste” meinen wir “den effizientesten” im Sinne einer minimalen Varianz. Was mit der Varianz eines Schätzers gemeint wird, wird ausführlich in Kapitel 11 erläutert.
Es gibt auch Varianten von OLS mit denen man die Abhängigkeit von den gerade aufgeführten Kernannahmen reduzieren kann. Das bedeutet aber auch, dass wann immer eine oder mehrere Annahmen verletzt ist, wir unseren Ergebnissen nur bedingt vertrauen können und einige Ergebnisse und Kennzahlen unserer Regression möglicherweise irreführend sind. An dieser Stelle ist es wichtig darauf hinzuweisen, dass wir eine Regression mit OLS schätzen können und keine Fehlermeldungen bekommen, auch wenn die Annahmen für OLS nicht erfüllt sind. Daher ist es immer wichtig, die Korrektheit der Annahmen selbst zu überprüfen und weitere Kennzahlen der Regression zu betrachten um die Ergebnisse unserer Schätzung besser einschätzen zu können. Während die Methoden zum Test der Annahmen in Kapitel 11 eingeführt werden, betrachten wir im Folgenden schon einmal generelle Gütezahlen für eine lineare Schätzung, die Sie bei jeder Anwendung von OLS zu Rate ziehen sollten.
10.3 Kennzahlen in der linearen Regression
10.3.1 Erklärte Varianz und das \(R^2\)
Als erstes wollen wir fragen, ‘wie gut’ unser geschätztes Modell unsere Daten erklären kann. In der ökonometrischen Praxis können wir dazu fragen, wie viel ‘Variation’ der abhängigen Variable \(Y_i\) durch die Regression erklärt wird. Als Maß für die Variation wird dabei die Summe der quadrierten Abweichungen von \(Y_i\) von seinem Mittelwert verwendet, auch \(TSS\) (für engl. Total Sum of Squares - ‘Summe der Quadrate der Totalen Abweichungen’) genannt:
\[TSS=\sum_{i=1}^n(Y_i-\bar{Y})^2\] In R:
tss <- sum((datensatz$y - mean(datensatz$y))**2)
tss#> [1] 3.30012Diese Werte sind in Abbildung 10.3 für unseren Beispieldatensatz von oben grafisch dargestellt:

Abbildung 10.3: Werte für die Summe der totalen Abweichungen (TSS).
Die TSS wollen wir nun aufteilen in eine Komponente, die in unserer Regression erklärt wird, und eine Komponente, die nicht erklärt werden kann. Bei letzterer handelt es sich um die Abweichungen der geschätzten Werte \(\hat{Y_i}\) und den tatsächlichen Werten \(Y_i\), den oben definierten Residuen \(e_i\). Entsprechend definieren wir die Residual Sum of Squares (RSS) (dt.: Residuenquadratsumme) als:
\[RSS=\sum_i^ne_i^2\] In R:
rss <- sum(schaetzung[["residuals"]]**2)
rss#> [1] 2.35148Diese sehen wir in Abbildung 10.4.

Abbildung 10.4: Abweichungen der geschätzen Werten und den tatsächlichen Werten, i.e. den Residuen (RSS).
Was noch fehlt sind die Explained Sum of Squares (ESS) (dt. Summe der Quadrate der Erklärten Abweichungen), also die Variation in der abhängigen Variable, die durch die Regression erklärt wird. Dabei handelt es sich um die quadrierte Differenz zwischen \(\bar{Y}\) und den geschätzten Werten \(\hat{Y}\):
\[ESS=\sum_{i=1}^n(\hat{Y}_i-\bar{Y})^2\] Diese ergibt sich in R als:
ess <- sum((schaetzung[["fitted.values"]] - mean(datensatz$y))**2)
ess#> [1] 0.94864Und grafisch wie in Abbildung 10.5 beschrieben.
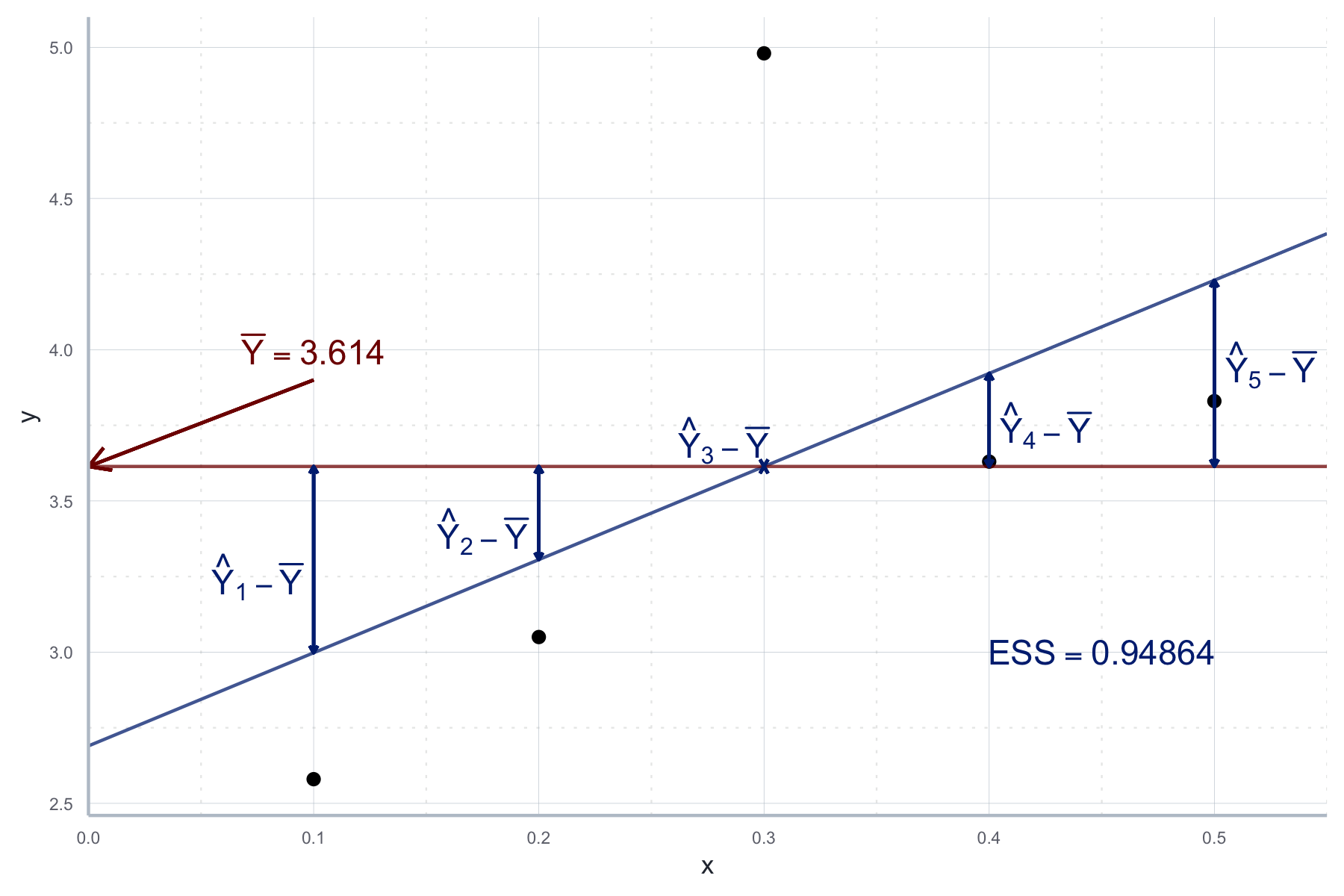
Abbildung 10.5: Variation in der abhängigen Variable, die durch die Regression erklärt wird (ESS).
Für die drei gerade eingeführten Teile der Gesamtvarianz gilt im Übrigen:
\[TSS=ESS+RSS\]
Aus diesen Werten können wir nun das Bestimmtheitsmaß \(R^2\) berechnen, welches Informationen darüber gibt, welchen Anteil der Variation in \(Y_i\) durch unser Modell erklärt wird:
\[R^2=\frac{ESS}{TSS}=1-\frac{RSS}{TSS}\]
Wir können das für unseren Anwendungsfall natürlich händisch berechnen:
r_sq_manual <- ess / tss
r_sq_manual#> [1] 0.2874562Leider wird diese Größe im Output von lm() direkt nicht ausgegeben.
Wir können aber einen ausführlicheren Output unserer Regression mit der Funktion
summary() erstellen, dort ist das \(R^2\) dann auch enthalten:
info_schaetzung <- summary(schaetzung)
info_schaetzung[["r.squared"]]#> [1] 0.2874562In unserem Fall erklärt unser Modell also ca. 29 Prozent der Gesamtvarianz der erklärten Variable.
In einer sozialwissenschaftlichen Anwendung wäre das nicht so wenig, denn aufgrund der vielen Faktoren, die hier eine Rolle spielen, darf man keine zu hohen Werte für \(R^2\) erwarten. Vielmehr legen sehr hohe Werte eine gewisse Skepsis nahe, ob nicht eher ein tautologischer Zusammenhang geschätzt wurde.
Ein großer Nachteil vom \(R^2\) ist, dass es größer wird sobald wir einfach mehr erklärende Variablen in unsere Regression aufnehmen. Warum? Eine neue Variable kann unmöglich \(TSS\) verändern (denn die erklärenden Variablen kommen in der Formel für TSS nicht vor), aber erhöht immer zumindest ein bisschen die ESS. Wenn unser alleiniges Ziel also die Maximierung von \(R^2\) wäre, dann müssten wir einfach ganz viele erklärenden Variablen in unser Modell aufnehmen. Das kann ja nicht Sinn sozioökonomischer Forschung sein!
Zur Lösung dieses Problems wurde das adjustierte \(R^2\) entwickelt, was bei Regressionen auch standardmäßig angegeben wird. Hier korrigieren wir das \(R^2\) mit Hilfe der Freiheitsgrade (engl. degrees of freedom). Die Freiheitsgerade sind die Differenz zwischen Beobachtungen und Anzahl der zu schätzenden Parameter und werden in der Regel mit \(df\) bezeichnet.
Das adjustierte \(R^2\), häufig als \(\bar{R}^2\) bezeichnet, ist definiert als:
\[\bar{R}^2=1-\frac{\sum_{i=1}^n\epsilon^2/(N-K-1)}{\sum_{i=1}^n(Y_i-\bar{Y})^2/(N-1)}\] In unserem Fall hier ist \(N=5\) und \(K=2\), da mit \(\beta_0\) und \(\beta_1\) zwei Parameter geschätzt werden. Um dieses Maß aus unserem Ergebnisobjekts auszugeben schreiben wir:
info_schaetzung[["adj.r.squared"]]#> [1] 0.04994162Leider hat es keine so eindeutige Interpretation wie das \(R^2\), aber es sollte immer gemeinsam mit letzterem beachtet werden. Häufig vergleicht man das \(\bar{R}^2\) vor und nach der Inklusion einer weiteren erklärenden Variable. Wenn \(\bar{R}^2\) steigt geht man häufig davon aus, dass sich die Inklusion auszahlt, allerdings sind das ‘nur’ Konventionen. Man sollte nie eine Variabel ohne gute theoretische Begründung aufnehmen! Zudem bietet sich \(\bar{R}^2\) an, wenn man zwei Modelle des gleichen Untersuchungsgegenstandes miteinander vergleichen will - in diesem Fall geht es nur darum, welches Modell das höhere \(\bar{R}^2\) hat, weniger um den konkreten Wert.
10.3.2 Hypothesentests und statistische Signifikanz
Wie sicher können wir uns mit den geschätzten Parametern für \(\beta_0\) und \(\beta_1\) sein? Wenn z.B. \(\hat{\beta}_1>0\), bedeutet das wirklich, dass wir einen positiven Effekt gefunden haben? Immerhin sind ja unsere Fehler ZV und vielleicht haben wir einfach zufällig eine Stichprobe erhoben, wo der Effekt von \(x_1\) positiv erscheint, tatsächlich aber kein Effekt existiert? Um die Unsicherheit, die mit der Parameterschätzung einhergeht, zu quantifizieren können wir uns die Annahme, dass unsere Fehler normalverteilt sind, zu Nutze machen und testen wie plausibel die tatsächliche Existenz eines Effekts ist.
Wir verlassen nun also das Gebiet der reinen Parameterschätzung und beschäftigen uns mit Hypothesentests und Konfidenzintervallen für unsere Schätzer \(\hat{\beta}_0\) und \(\hat{\beta}_1\). Das ist analog zu den in Kapitel 9 zur schließenden Statistik besprochenen Herangehensweisen.
Wir wissen bereits, dass es sich bei unseren Schätzern \(\hat{\beta}_0\) und \(\hat{\beta}_1\) um ZV handelt. Aber welcher Verteilung folgen sie? Da wir im Rahmen des OLS Modells annehmen, dass der Erwartungswert der Fehler gleich null ist (siehe Abschnitt 10.2.3), können wir schreiben:
\[\hat{\beta}_0 \propto \mathcal{N}\left(\beta_0, \sigma^2\left( \frac{1}{n} + \frac{\bar{x}^2}{SS_X}\right) \right), \quad SS_X=\sum_{i=1}^n(x_i-\bar{x})^2\\ \hat{\beta}_1 = \mathcal{N}\left(\beta_1, \frac{\sigma^2}{SS_X}\right)\]
Da \(\mathbb{E}(\hat{\beta_i})=\beta_i\) sagen wir, dass die Schätzer erwartungstreu sind - wir also erwarten, dass Sie im Mittel den wahren Wert für den Parameter schätzen.
Es ist dann plausibel die Genauigkeit oder Effizienz eines Schätzers durch seine Varianz zu messen: wenn ein Schätzer eine große Varianz hat bedeutet das, dass wir bei dem einzelnen Schätzwert eine große Unsicherheit haben, ob der Schätzer tatsächlich nahe an seinem Erwartungswert liegt. Am besten kann man das an einem simulierten Beispiel illustrieren.
Beispiel: Die Varianz von \(\hat{\beta}_1\): Im Folgenden kreieren wir einen künstlichen Datensatz, bei dem wir den wahren datengenerierenden Prozess kennen. Diesen beschreiben wir durch folgende Gleichung:
\[Y_i=\beta_0+\beta_1 x_i + \epsilon_i, \quad \epsilon_i\propto\mathcal{N}(0,5)\]
Wenn wir nun mit diesem Prozess mehrere Datensätze kreieren, sieht natürlich jeder Datensatz anders aus. Schließlich sind die \(\epsilon_i\) zufällig. Dennoch wissen wir, dass, da unsere Schätzer erwartungstreu sind, sie im Mittel die wahren Werte von \(\beta_0\) und \(\beta_1\) treffen sollten. Aber wie sehr streuen die geschätzten Werte um diesen wahren Wert? Zunächst erstellen wir den künstlichen Datensatz. Dazu spezifizieren wir zunächst die Grundstruktur des datengenerierenden Prozess:
set.seed(123)
true_DGP <- function(x, b0, b1){
y <- b0 + b1*x + rnorm(length(x), 0, 5)
return(y)
}
beta_0_wahr <- 3
beta_1_wahr <- 2
sample_size <- 100
x <- runif(sample_size, 0, 10)Nun erstellen wir mit Hilfe einer Schleife 1000 Realisierungen der Daten. Wir können uns das wie 1000 Erhebungen vorstellen. Für jede dieser Realisierungen schätzen wir dann die lineare Regressionsgleichung von oben:
set.seed(123)
n_datensaetze <- 1000
beta_0_estimates <- rep(NA, n_datensaetze)
beta_1_estimates <- rep(NA, n_datensaetze)
for (i in 1:n_datensaetze){
daten_satz <- data.frame(
x = x,
y = true_DGP(x, beta_0_wahr, beta_1_wahr)
)
schaetzung_2 <- lm(y~x, data = daten_satz)
beta_0_estimates[i] <- schaetzung_2[["coefficients"]][1]
beta_1_estimates[i] <- schaetzung_2[["coefficients"]][2]
}Nun können wir die Streuung der Schätzer in Abbildung 10.6 ablesen.

Abbildung 10.6: Vergleich der Effizienz zweier Schätzer über ihre jeweilige Streuung.
Wie wir sehen, treffen die Schätzer im Mittel den richtigen Wert, streuen aber auch. Die Varianz gibt dabei die Breite des jeweiligen Histograms an und je stärker die relativen Häufigkeiten des geschätzten Wertes um den wahren Wert konzentriert sind, also desto geringer die Varianz, desto genauer und somit effizienter ist der Schätzer.
Ein Maß für die Genauigkeit eines Schätzers ist sein Standardfehler. Für \(\hat{\beta}_1\) ist dieser wie oben beschrieben definiert als \(\frac{\sigma}{\sqrt{SS_X}}\). Da \(\sigma\) (die Varianz der Fehler) nicht bekannt ist, müssen wir sie aus den Daten schätzen. Das geht mit \(\frac{1}{n-2}\sum_{i=1}^ne_i^2\), wobei die detaillierte Herleitung hier nicht diskutiert wird. Grundsätzlich handelt es sich hier um die empirische Varianz. Das \(n-2\) kommt von den um zwei reduzierten Freiheitsgraden dieser Schätzung.
Dieser Standardfehler ist ein erstes Maß für die Genauigkeit des Schätzers. Er wird aufgrund seiner Wichtigkeit auch in der Summary jeder Schätzung angegeben. Hier betrachten wir die Schätzung aus dem einführenden Beispiel:
summary(schaetzung_bip)#>
#> Call:
#> lm(formula = Konsum ~ BIP, data = bip_daten)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.057813 -0.007137 -0.002679 0.015034 0.051435
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.19021 0.03478 5.468 3.41e-05 ***
#> BIP 0.66552 0.01296 51.341 < 2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.02353 on 18 degrees of freedom
#> Multiple R-squared: 0.9932, Adjusted R-squared: 0.9928
#> F-statistic: 2636 on 1 and 18 DF, p-value: < 2.2e-16Sie sind hier unter Std. Error zu finden. Wir können diese Information jedoch
noch weiter verwenden und Hypothesen im
Zusammenhang mit den Schätzern testen. Eine besonders relevante Frage ist immer
ob ein bestimmter Schätzer signifikant
von 0 verschieden ist. Dazu können wir fragen: “Wie wahrscheinlich ist es,
gegeben der Daten, dass \(\beta_i\) gleich Null ist?”.
Das ist die klassische Frage für einen Hypothesentest88 mit \(H_0: \beta_0=0\) und \(H_1: \beta_0 \neq 0\).
Für einen Hypothesentest brauchen wir zunächst eine Teststatistik, also die Verteilung für den Schätzer wenn \(H_0\) wahr wäre. Da wir annehmen, dass die Fehlerterme in unserem Fall normalverteilt sind, ist das in unserem Falle eine \(t\)-Verteilung mit \(n-2\) Freiheitsgraden.89 Damit können wir überprüfen wie wahrscheinlich unser Schätzwert unter der \(H_0\) wäre. Wenn er sehr unwahrscheinlich wäre, würden wir \(H_0\) verwerfen.
Die Wahrscheinlichkeit, dass wir unseren Schätzer gefunden
hätten, wenn \(H_0\) wahr wäre wird durch den \(p\)-Wert des Schätzers angegeben.
Dieser findet sich in der Spalte Pr(>|t|).
In unserem Fall mit \(\hat{\beta}_1\) ist dieser Wert mit \(2\cdot 10^{-16}\)
extrem klein. Das bedeutet, wenn \(H_0: \beta_1=0\) wahr wäre, würden wir unseren
Wert für \(\hat{\beta}_1\) mit einer Wahrscheinlichkeit nahe Null beobachten.
Es erscheint daher sehr unplausibel, dass \(\beta_1=0\).
Tatsächlich würden wir diese Hypothese auf quasi jedem beliebigen
Signifikanzniveau verwerfen. Daher ist der Schätzer in der Zusammenfassung mit
drei Sternen gekennzeichnet:
summary(schaetzung_bip)#>
#> Call:
#> lm(formula = Konsum ~ BIP, data = bip_daten)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.057813 -0.007137 -0.002679 0.015034 0.051435
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.19021 0.03478 5.468 3.41e-05 ***
#> BIP 0.66552 0.01296 51.341 < 2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.02353 on 18 degrees of freedom
#> Multiple R-squared: 0.9932, Adjusted R-squared: 0.9928
#> F-statistic: 2636 on 1 and 18 DF, p-value: < 2.2e-16Grundsätzlich gilt, dass wir \(H_0: \beta_i = 0\) auf dem \(\alpha\)-Signifikanzniveau verwerfen können wenn \(p<1-\alpha\). Wenn wir \(H_0: \beta_i\) auf dem Signifikanzniveau von mindestens \(\alpha=0.05\) verwerfen können, sprechen wir von einem signfikanten Ergebnis. In unserem Beispiel der Konsumfunktion sind also sowohl die Schätzer \(\beta_0\) und \(\beta_1\) hochsignifikant und wir können, under den oben getroffenen Annahmen, mit großer Sicherheit davon ausgehen, dass beide von Null verschieden sind.
Dabei ist jedoch wichtig darauf hinzuweisen, dass statistische Signifikanz nicht mit sozioökonomischer Relevanz zu tun hat: ein Effekt kann hochsignifikant, aber extrem klein sein. Dennoch ist die Signifikanz eine wichtige und häufig verwendete Kennzahl für jede lineare Regression. Gleichzeitig ist die wissenschaftliche Praxis, nur Studien mit signifikanten Ergebnissen ernst zu nehmen, sehr problematisch, Stichwort p-Hacking.
10.3.3 Konfidenzintervalle für die Schätzer
Ausgehend von den Überlegungen zur Signifikanz können wir nun Konfidenzintervalle für unsere Schätzer konstruieren. Wie im Kapitel 9 zur schließenden Statistik genauer erläutert besteht ein ein Konfidenzintervall \(I_{\alpha}\) aus allen geschätzten Parameterwerten, für die wir bei einem zweiseitigen Hypothesentest zum Signifikanzniveau \(\alpha\) die Nullhypothese \(\beta_i=0\) nicht verwerfen können.
Um diese Intervalle für eine Schätzung in R zu konstruieren verwenden wir die
Funktion confint, die als erstes Argument das geschätzte Modell und als
Argument level das Signifikanzniveau \(1-\alpha\) akzeptiert:
confint(schaetzung_bip, level=0.95)#> 2.5 % 97.5 %
#> (Intercept) 0.1171319 0.2632874
#> BIP 0.6382880 0.6927551Für \(\hat{\beta}_1\) ist das 95%-Konfidenzintervall also \([0.69, 0.72]\). Das bedeutet, wenn der zugrundeliegende Datengenerierungsprozess sehr häufig wiederholt werden würde, dann würden 95% der so für \(\hat{\beta}_1\) berechneten 95%-Konfidenzintervalle \(\beta_1\) enthalten.
10.3.4 Zur Rolle der Stichprobengröße
Um die Rolle der Stichprobengröße besser beurteilen zu können, verwenden wir hier einen künstlich hergestellten Datensatz für den wir die ‘wahren’ Werte \(\beta_0\) und \(\beta_1\) kennen:90
set.seed(123)
wahres_b0 <- 3
wahres_b1 <- 1.4
stichproben_n <- 50
x <- 1:stichproben_n * 0.1
fehler <- rnorm(stichproben_n, mean = 0, sd = 3)
y <- rep(NA, stichproben_n)
for (i in 1:stichproben_n){
y[i] <- wahres_b0 + wahres_b1*x[i] + fehler[i]
}
datensatz <- data.frame(
x = x,
y = y
)Wie wir in Abbildung 10.7 sehen ist die geschätzte Gerade nicht exakt deckungsgleich zur ‘wahren’ Gerade, aber doch durchaus nahe dran.
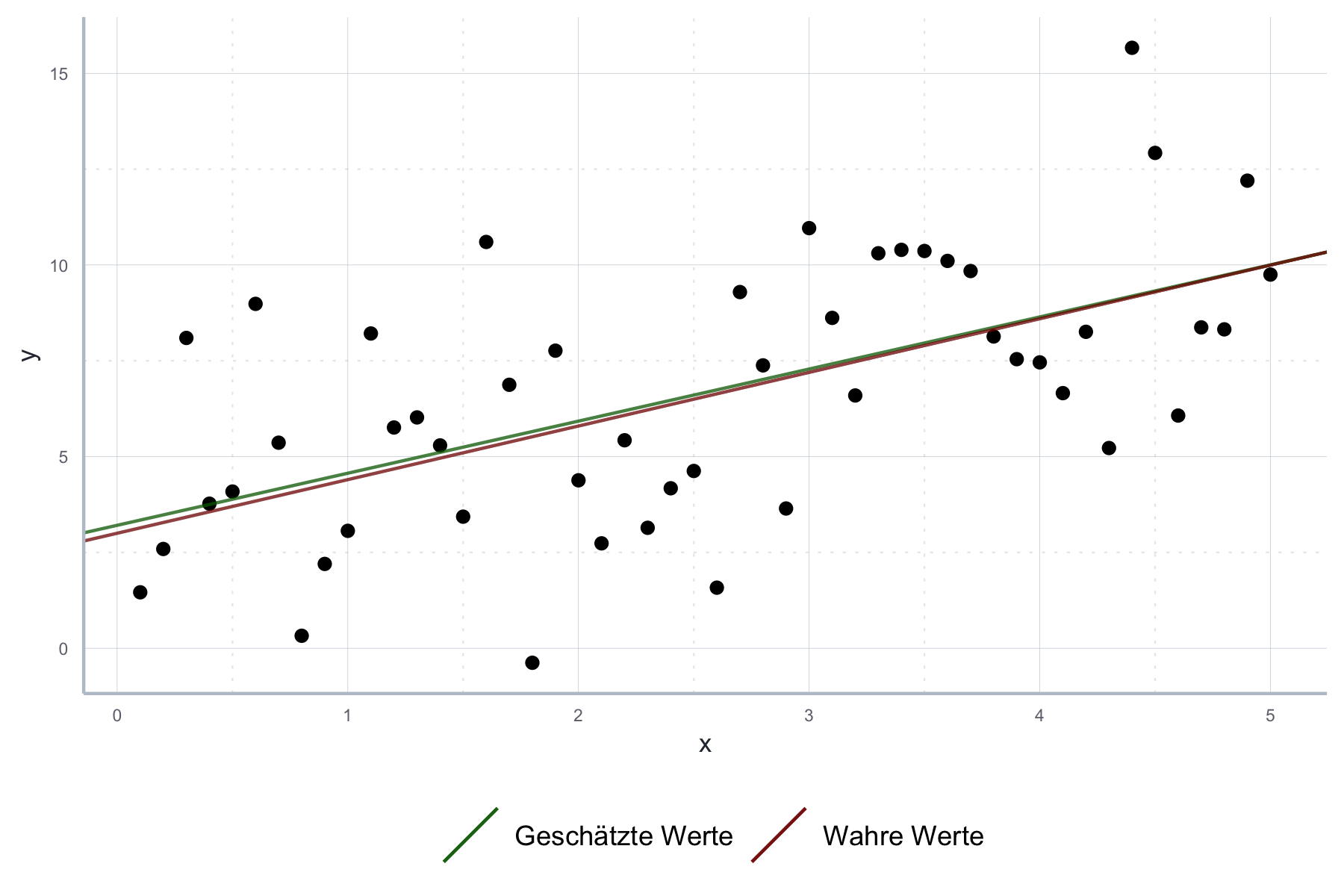
Abbildung 10.7: Vergleich der geschätzten und wahren Gerade unserer Stichprobe.
Grundsätzlich gilt, dass die erwartete Deckung der beiden dann höher ist wenn (1) die Annahmen für die einfache lineare Regression erfüllt sind und (2) die Stichprobe groß ist. Im Moment sind wir in einer Luxussituation, da wir die ‘wahre’ Gerade kennen: wir haben ja den Datensatz, für den wir die Gerade schätzen, selbst erstellt. In der Praxis bleibt uns nichts anderes üblich als (1) so gut es geht zu überprüfen und die restliche Unsicherheit so gut es geht zu quantifizieren. Im Folgenden wollen wir uns genauer anschauen welche Methoden uns dafür zur Verfügung stehen. Vorher wollen wir uns aber noch in Abbildung 10.8 ansehen, wie eine größere Stichprobe die Schätzgenauigkeit beeinflusst.
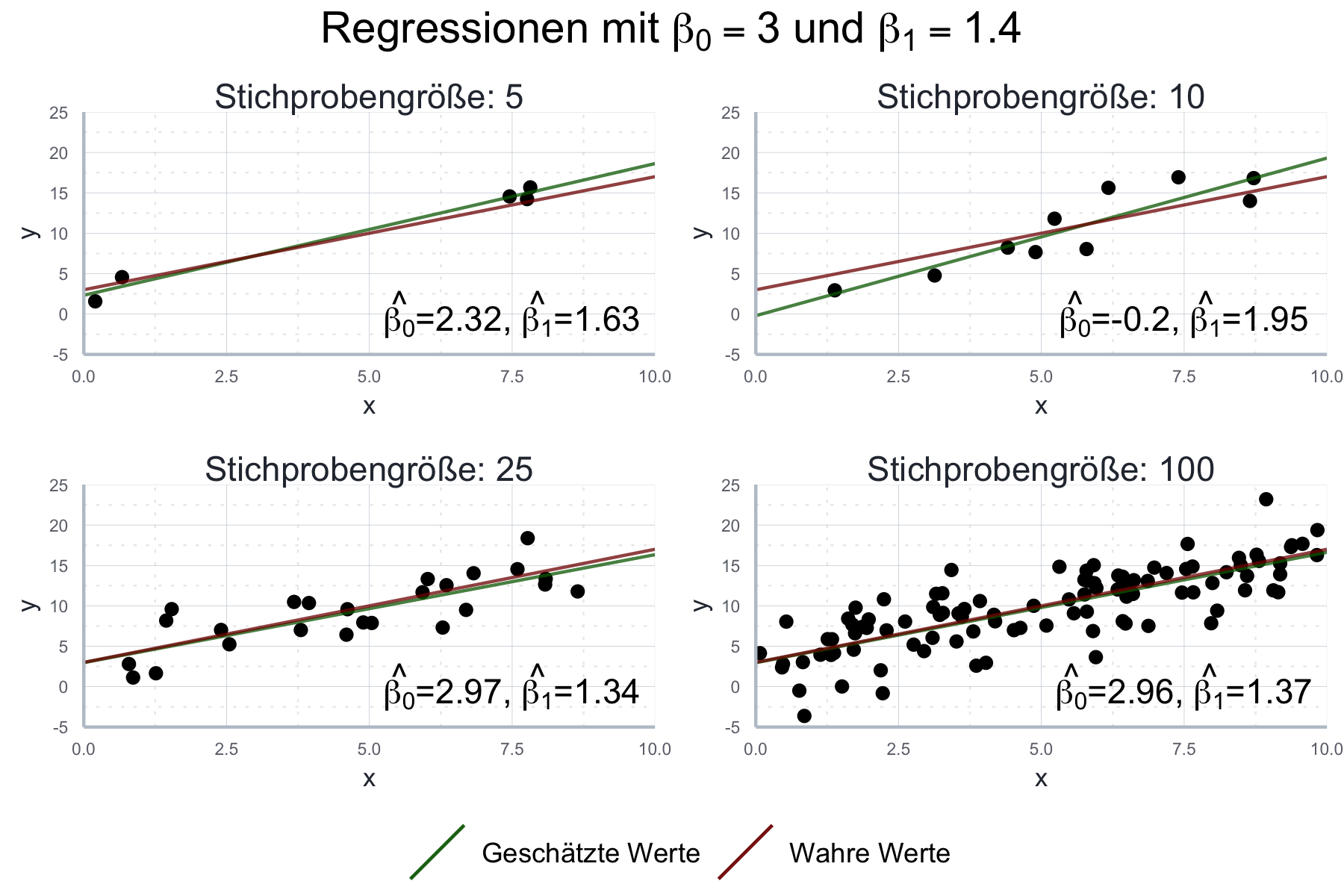
Abbildung 10.8: Vergleich der geschätzten Parameterwerte mit den wahren Werten unter verschiedenen Stichprobengrößen.
10.4 Multiple lineare Regression
Zum Abschluss wollen wir noch das bislang besprochene für den Fall von mehreren erklärenden Variablen generalisieren. In der Praxis werden Sie nämlich so gut wie immer mehr als eine erklärende Variable verwenden. Zwar sind die resultierenden Plots häufig nicht so einfach zu interpretieren wie im Fall der einfachen Regression, das Prinzip ist jedoch quasi das gleiche. Zudem ist die Implementierung in R nicht wirklich schwieriger.
Im Folgenden wollen wir den uns bereits aus früheren Kapiteln bekannten Beispieldatensatz verwenden, in dem Informationen über die Preise von ökonomischen Journalen gesammelt sind:
journal_data <- fread(here("data/tidy/journaldaten.csv")) %>%
select(Titel, Preis, Seitenanzahl, Zitationen)
head(journal_data)#> Titel Preis Seitenanzahl
#> 1: Asian-Pacific Economic Literature 123 440
#> 2: South African Journal of Economic History 20 309
#> 3: Computational Economics 443 567
#> 4: MOCT-MOST Economic Policy in Transitional Economics 276 520
#> 5: Journal of Socio-Economics 295 791
#> 6: Labour Economics 344 609
#> Zitationen
#> 1: 21
#> 2: 22
#> 3: 22
#> 4: 22
#> 5: 24
#> 6: 24In einer einfachen linearen Regression könnten wir z.B. folgendes Modell schätzen:
\[PREIS_i = \beta_0 + \beta_1 SEITEN + \epsilon\]
Das würden wir mit folgendem Befehl in R implementieren:
reg <- lm(Preis~Seitenanzahl, data=journal_data)
summary(reg)#>
#> Call:
#> lm(formula = Preis ~ Seitenanzahl, data = journal_data)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -1157.56 -190.54 -40.72 179.59 1329.30
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 56.74315 53.85199 1.054 0.293
#> Seitenanzahl 0.43610 0.05757 7.575 1.89e-12 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 336.5 on 178 degrees of freedom
#> Multiple R-squared: 0.2438, Adjusted R-squared: 0.2395
#> F-statistic: 57.38 on 1 and 178 DF, p-value: 1.888e-12Allerdings ergibt es auch Sinn anzunehmen, dass beliebte Journale teurer sind. Daher würden wir gerne die Anzahl der Zitationen in das obige Modell als zweite erklärende Variable aufnehmen. In diesem Fall würden wir mit einem multiplen linearen Modell arbeiten:
\[PREIS_i = \beta_0 + \beta_1 SEITEN + \beta_2 ZITATE + \epsilon\]
Tatsächlich ist die einzige Änderungen, die wir auf der technischen Seite machen müssen, die Inklusion der neuen erklärenden Variable in die Schätzgleichung:
reg <- lm(Preis~Seitenanzahl + Zitationen, data=journal_data)Hierbei ist zu beachten, dass das + nicht im additiven Sinne gemeint ist,
sondern in der Logik einer Regressionsgleichung.
Wenn wir uns die Zusammenfassung dieses Objekts anschauen, sehen wir einen sehr ähnlichen Output wie für den einfachen linearen Fall, nur dass wir eine weitere Zeile für die neue erklärende Variable haben:
summary(reg)#>
#> Call:
#> lm(formula = Preis ~ Seitenanzahl + Zitationen, data = journal_data)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -1346.70 -173.48 -38.83 138.32 1259.00
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -3.72002 52.80969 -0.070 0.944
#> Seitenanzahl 0.59413 0.06477 9.173 < 2e-16 ***
#> Zitationen -0.10872 0.02393 -4.544 1.02e-05 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 319.3 on 177 degrees of freedom
#> Multiple R-squared: 0.3228, Adjusted R-squared: 0.3151
#> F-statistic: 42.18 on 2 and 177 DF, p-value: 1.049e-15Zwei Punkte sind bei der multiplen Regression zu beachten: Erstens sind die geschätzten Effekte als isolierte Effekte zu interpretieren, also in einer Situation in der alle anderen erklärenden Variablen fix gehalten werden. Das ist die berühmte ceteris paribus Formel.
Der geschätzte Wert für Seitenanzahl sagt uns dementsprechend:
“Ceteris paribus, also alle anderen Einflussfaktoren fix gehalten, geht ein
um eine Seite dickeres Journal mit einem um \(0.6\) Dollar höherem Abo-Preis einher.”
Beachten Sie den relevanten Unterschied zur einfachen Regression,
die sehr wahrscheinlich unter dem oben angesprochenen omitted variable bias
gelitten hat.
Der zweite zu beachtende Aspekt bezieht sich auf die Korrelation der verschiedenen erklärenden Variablen. Die Annahmen für OLS schließen an sich nur so genannte perfekte Kollinearität (siehe Abschnitt 10.2.3) aus. Das heißt die Situation in der eine erklärende Variable eine perfekte lineare Transformation einer anderen erklärenden Variable ist. Problematisch sind aber auch schon geringere, aber immer noch hohe Korrelationen: denn je stärker die erklärenden Variablen untereinander korrelieren, desto größer werden die Standardfehler unserer Schätzer. Mit diesem Problem werden wir uns im folgenden Kapitel noch genauer auseinandersetzen.
10.5 Zum Ablauf einer Regression
Insgesamt ergibt sich aus den eben beschriebenen Schritten also folgendes Vorgehen bei einer Regression:
Aufstellen des statistischen Modells
Erheben und Aufbereitung der Daten
Schätzen des Modells
Überprüfung der Modellannahmen (dazu mehr im Kapitel 11)
Inspektion der relevanten Kennzahlen wie \(R^2\) und der statistischen Signifikanz der geschätzten Werte; falls relevant: Angabe von Konfidenzintervallen
Dabei handelt es sich natürlich um ein eher stilisiertes Beispiel: Der Konsum ist ja Teil der Definition des BIP, weswegen ein starker Zusammenhang keine Überraschung und eine lineare Regression in diesem Kontext sogar sehr irreführend wäre - mehr dazu in Kapitel 11. Zusammenhänge, die in der Forschung betrachtet werden, sind oft weit weniger trivial und so gut wie immer steht auf der rechten Seite mehr als eine Variable. Alles was Sie für die einfache lineare Regression lernen gilt aber fast genauso für die multiple lineare Regression, die wir dann später in Abschnitt 10.4 kennen lernen werden.↩︎
D.h. die Fehler sind unabhängig voneinander und folgen alle der gleichen Verteilung.↩︎
Wenn Sie Schwierigkeiten mit dem Konzept einer ZV haben, schauen Sie doch noch einmal in Kapitel 7 nach.↩︎
Wenn Ihnen das Konzept eines Schätzers sehr fremd ist, schauen Sie noch mal in das Kapitel 9 zu schließender Statistik.↩︎
Warum summiert man nicht die Absolutwerte der Abweichungen, sondern ihre quadrierten Werte? Das hat technische Gründe: mit quadrierten Werten lässt sich einfach leichter rechnen als mit Absolutwerten.↩︎
Jede*r Interessierte findet die genaue Herleitung im Kapitel zu linearen Algebra.↩︎
Was das genau bedeutet wird im Detail in Kapitel 11 erläutert.↩︎
Lesen Sie noch einmal im Kapitel @ref(#stat-rep) zur schließenden Statistik nach, wenn Sie nicht mehr wissen was ein Hypothesentest ist.↩︎
Warum jetzt genau eine \(t\)-Verteilung und keine Normalverteilung? Das liegt daran, dass wir die Varianz unserer Fehler \(\sigma\) nicht beobachten können und durch \(\hat{\sigma}\) geschätzt haben. Das führt dazu, dass die resultierende Teststatistik nicht mehr normalverteilt ist. Mit zunehmendem Stichprobenumfang wird die Abweichung immer irrelevanter, jedoch ist die t-Verteilung so einfach zu handhaben, dass man sie eigentlich immer benutzen kann.↩︎
Die Befehle sollten Ihnen weitgehen bekannt sein. Die Funktion
set.seed()verwenden wir um den Zufallszahlengenerator von R so zu kalibrieren, dass bei jedem Durchlaufen des Skripts die gleichen Realisierungen der ZV gezogen werden und die Ergebnisse somit reproduzierbar sind.↩︎