Chapter 7 Grundlagen der Wahrscheinlichkeitstheorie

In diesem Kapitel werden einige grundlegende Konzepte der Wahrscheinlichkeitstheorie eingeführt, bzw. wiederholt. Die zentralen Themen auf die wir uns fokussieren werden sind dabei:

• Der Zusammenhang zwischen Wahrscheinlichkeitstheorie und Statistik
• Grundbegriffe der Wahrscheinlichkeitstheorie und Statistik
• Zufallsvariablen
• Diskrete und stetige Verteilungen einzelner und mehrerer Zufallsvariablen

Grundkonzepte der deskriptiven und schließenden Statistik (insb. Parameterschätzung, Hypothesentests und die Berechnung von Konfidenzintervallen) werden in den beiden folgenden Kapiteln zur deskriptiven und schließenden Statistik (siehe Kapitel 8 und Kapitel 9 behandelt.

Verwendete Pakete

library(here)
library(tidyverse)
library(ggpubr)
library(latex2exp)
library(data.table)
library(viridis)
library(icaeDesign)

7.1 Einleitung: Wahrscheinlichkeitstheorie und Statistik

Statistik und Wahrscheinlichkeitstheorie sind untrennbar miteinander verbunden. In der Wahrscheinlichkeitstheorie beschäftigt man sich mit Modellen von Zufallsprozessen, also Prozessen, deren Ausgang nicht exakt vorhersehbar ist. Häufig spricht man von Zufallsexperimenten.

Die Wahrscheinlichkeitstheorie entwickelt dabei Modelle, welche diese Zufallsexperimente und deren mögliche Ausgänge beschreiben und dabei den möglichen Ausgängen Wahrscheinlichkeiten zuordnen. Diese Modelle werden Wahrscheinlichkeitsmodelle genannt.

In der Statistik versuchen wir anhand von beobachteten Daten herauszufinden, welches Wahrscheinlichkeitsmodell gut geeignet ist, den die Daten generierenden Prozess (data generating process - DGP) zu beschreiben. Das ist der Grund warum man für Statistik auch immer Kenntnisse der Wahrscheinlichkeitstheorie braucht.

Kurz gesagt: in der Wahrscheinlichkeitstheorie wollen wir mit Hilfe von Wahrscheinlichkeitsmodellen Daten vorhersagen, in der Statistik mit Hilfe bekannter Daten Rückschlüsse auf die zugrundeliegenden Wahrscheinlichkeitsmodelle ziehen.

7.2 Grundbegriffe der Wahrscheinlichkeitstheorie

7.2.1 Wahrscheinlichkeitstheoretische Modelle

Ein wahrscheinlichkeitstheoretisches Modell besteht immer aus den folgenden drei Komponenten:

Ergebnisraum: diese Menge \(\Omega\) enthält alle möglichen Ergebnisse des modellierten Zufallsexperiments. Das einzelne Ergebnis bezeichnen wir mit \(\omega\).

Beispiel: Handelt es sich bei dem Zufallsexperiment um das Werfen eines normalen sechseitigen Würfels, so gilt \(\Omega=\{1,2,3,4,5,6\}\). Wenn der Würfel gefallen ist, bezeichnen wir die oben liegende Zahl als das Ergebnis \(\omega\) des Würfelwurfs, wobei hier gilt \(\omega_1=\) “Der Würfel zeigt 1”, u.s.w.

Ereignisse: unter Ereignissen \(A, B, C,...\) verstehen wir die Teilmengen des Ergebnisraums. Ein Ereignis enthält ein oder mehrere Elemente des Ergebnisraums. Enthält ein Ereignis genau ein Element, sprechen wir von einem Elementarereignis.

Beispiel: “Es wird eine gerade Zahl gewürfelt” ist ein mögliches Ereignis im oben beschriebenen Zufallsexperiment. Das Ereignis - nennen wir es hier \(A\) - tritt ein, wenn ein Würfelwurf mit dem Ergebnis “2”, “4” oder “6” endet. Also: \(A=\{\omega_2, \omega_4, \omega_6\}\). Das Ereignis \(B\) “Es wird eine 2 gewürfelt” tritt nur ein, wenn das Ergebnis des Würfelwurfs eine 2 ist: \(B=\{\omega_2\}\). Entsprechend nennen wir es ein Elementarereignis.

Da es sich bei Ereignissen um Mengen handelt können wir die typischen mengentheoretischen Konzepte wie ‘Vereinigung’, ‘Differenz’ oder ‘Komplement’ zu ihrer Beschreibung verwenden. Diese sind in Tablle 7.1 zusammengefasst:

Tabelle 7.1: Mengentheoretische Konzepte und ihre Übersetzungen.

Konzept	Symbol	Übersetzung
Schnittmenge	\(A\cap B\)	\(A\) und \(B\)
Vereinigung	\(A\cup B\)	\(A\) und/oder \(B\)
Komplement	\(A^c\)	Nicht \(A\)
Differenz	\(A \setminus B = A\cap B^c\)	\(A\) ohne \(B\)

Wahrscheinlichkeiten: jedem Ereignis \(A\) wird eine Wahrscheinlichkeit \(\mathbb{P}(A)\) zugeordnet. Wahrscheinlichkeiten können aber nicht beliebige Zahlen sein. Vielmehr müssen sie im Einklang mit den drei Axiomen von Kolmogorow stehen:

1. Für jedes Ereignis \(A\) gilt: \(0\leq\mathbb{P}(A)\leq1\)

2. Das sichere Ereignis \(\Omega\) umfasst den ganzen Ergebnisraum und es gilt entsprechend \(\mathbb{P}(\Omega)=1\).

3. Es gilt: \(\mathbb{P}(A\cup B) = \mathbb{P}(A)+\mathbb{P}(B)\) falls \(A\cap B=\emptyset\), also wenn sich A und B gegenseitig ausschließen.

Aus diesen Axiomen lassen sich eine ganze Menge Sätze heraus ableiten, auf die wir im Folgenden nicht weiter eingehen wollen. Die Grundidee ist aber, bestimmten Ereignissen von Anfang an bestimmte Wahrscheinlichkeiten zuzuordnen, und die Wahrscheinlichkeiten für andere Ereignisse dann aus den eben beschriebenen Regeln abzuleiten.

Je nach Art des Ergebnisraums \(\Omega\) unterscheiden wir zwei grundsätzlich verschiedene Arten von Wahrscheinlichkeitsmodellen: ist \(\Omega\) abzählbar handelt es sich um ein diskretes Wahrscheinlichkeitsmodell. Der Würfelwurf oder ein Münzwurf sind hierfür Beispiele: die Menge der möglichen Ergebnisse ist hier klar abzählbar.⁶⁴

Ist \(\Omega\) nicht abzählbar handelt es sich dagegen um ein stetiges Wahrscheinlichkeitsmodell. Ein Beispiel hierfür wäre das Fallenlassen von Steinen und die Messung der Falldauer. Die einzelnen Ereignisse wären dann die Falldauer und da wir die Zeiten in immer kleineren Intervallen angeben können, es also allein zwischen den Messungen “1 Sekunde” und “2 Sekunden” unendlich viele Zwischenschritte gibt, würde gelten, dass \(\Omega=\mathbb{R^+}\). Dabei handelt es sich um eine nicht abzählbare Menge.

Welches Modell für den konkreten Anwendungsfall vorzuziehen ist, muss auf Basis von theoretischen Überlegungen entschieden werden.

7.2.2 Stochastische Unabhängigkeit

Von Interesse ist häufig aus den Wahrscheinlichkeiten für zwei Ereignisse, \(A\) und \(B\), die Wahrscheinlichkeit für \(A\cap B\), also die Wahrscheinlichkeit, dass beide Ereignisse auftreten, zu berechnen. Leider ist das nur im Spezialfall der stochastischen Unabhängigkeit ohne Probleme möglich. Stochastische Unabhängigkeit kann immer dann sinnvollerweise angenommen werden, wenn zwischen den beteiligten Ereignissen kein kausaler Zusammenhang besteht. In diesem Fall gilt dann:

\[\mathbb{P}(A\cap B) = \mathbb{P}(A)\cdot\mathbb{P}(B)\]

Beispiel für stochastische Unabhängigkeit: Es ist plausibel anzunehmen, dass es keinen kausalen Zusammenhang zwischen zwei aufeinanderfolgenden Münzwürfen gibt. Entsprechend sind die Ereignisse \(A\): “Zahl im ersten Wurf” und \(B\): “Kopf im zweiten Wurf” stochastisch unabhängig und \(\mathbb{P}(A\cap B)=\mathbb{P}(A)\cdot \mathbb{P}(B)=\frac{1}{4}\).

Beispiel für stochastische Abhängigkeit: Ein anderer Fall liegt vor, wenn wir die Ereignisse \(C\): “Die Summe beider Würfe ist 6” und \(D\): “Der erste Wurf zeigt eine 2.” betrachten. Hier ist offensichtlich, dass ein kausaler Zusammenhang zwischen den beiden Würfen und den Ereignissen besteht. Es gilt: \(\mathbb{P}(C\cap D)=\mathbb{P}(\{2, 4\})=\frac{1}{36}\). Würden wir die Wahrscheinlichkeiten einfach multiplizieren erhielten wir allerdings \(\mathbb{P}(C)\cdot \mathbb{P}(D)=\frac{5}{36}\cdot\frac{1}{6}=\frac{5}{216}\), wobei \(\mathbb{P}(C)=\frac{5}{36}\).

7.2.3 Bedingte Wahrscheinlichkeiten

Ein weiteres wichtiges Konzept ist das der bedingten Wahrscheinlichkeit: die bedingte Wahrscheinlichkeit von \(A\) gegeben \(B\), \(\mathbb{P}(A|B)\), bezeichnet die Wahrscheinlichkeit für \(A\), wenn wir wissen, dass \(B\) bereits eingetreten ist.

Es gilt dabei:⁶⁵

\[\mathbb{P}(A|B)=\frac{\mathbb{P}(A\cap B)}{\mathbb{P}(B)}\]

Beispiel: Sei \(A\): “Der Würfel zeigt eine 6” und \(B\): “Der Würfelwurf zeigt eine gerade Zahl”. Wenn wir bereits wissen, dass \(B\) eingetreten ist, ist \(\mathbb{P}(A)\) nicht mehr \(\frac{1}{6}\), weil wir ja wissen, dass 1, 3 und 5 nicht auftreten können. Vielmehr gilt \(\mathbb{P}(A|B)=\frac{1/6}{1/2}=\frac{1}{3}\).

7.2.4 Der Satz von Bayes

Wenn wir aus der bedingten Wahrscheinlichkeit für \(A\) gegeben \(B\) die bedingte Wahrscheinlichkeit von \(B\) gegeben \(A\) berechnen wollen, also aus \(\mathbb{P}(A|B)\) den Ausdruck \(\mathbb{P}(B|A)\) ableiten möchten, dann müssen wir den Satz von Bayes anwenden - es gilt nämlich leider nicht notwendigerweise \(\mathbb{P}(A|B)=\mathbb{P}(B|A)\). Vielmehr gilt nach dem Satz von Bayes:

\[\mathbb{P}(A|B)=\frac{\mathbb{P}(A\cap B)}{\mathbb{P}(B)}=\frac{\mathbb{P}(B|A)\mathbb{P}(A)}{\mathbb{P}(B)}\]

Beispiel für die Anwendung von Bayes’ Theorem: Nehmen wir an, Claudius fährt an 70% der Tage mit dem Fahrrad in die Universität. Immer wenn Claudius mit dem Fahrrad fährt, ist er zu 80% pünktlich. Insgesamt ist er an 60% der Tage pünktlich. Wenn er nun heute pünktlich gekommen ist, wie hoch ist dann die Wahrscheinlichkeit, dass er mit dem Fahrrad gekommen ist? Um diese Frage zu beantworten können wir den Satz von Bayes verwenden. Sei \(A:\) “Claudius kommt mit dem Fahrrad” und \(B:\) “Claudius ist pünklich”. Dann gilt in jedem Falle \(\mathbb{P}(A)=0.7\), \(\mathbb{P}(B)=0.6\) sowie \(\mathbb{P}(B|A)=0.8\). Wir sind interessiert an \(\mathbb{P}(A|B)\), also der Wahrscheinlichkeit, dass Claudius mit dem Fahrrad gefahren ist, wenn er pünktlich war. Das können wir nun mit der oben beschriebene Formel herausfinden:

\[\mathbb{P}(A|B)=\frac{\mathbb{P}(B|A)\mathbb{P}(A)}{\mathbb{P}(B)}=\frac{0.8\cdot 0.7}{0.6}\approx 0.93\]

Die Wahrscheinlichkeit, dass Claudius mit dem Fahrrad gekommen ist beträgt also ca. 93 Prozent!

Herleitung von Bayes’ Theorem aus den Formeln für bedingte Wahrscheinlichkeiten Wir können Bayes’ Theorem aus den oben beschriebenen Formeln für bedingte Wahrscheinlichkeiten recht einfach herleiten. Wir wissen, dass

\[\mathbb{P}(A|B)=\frac{\mathbb{P}(A\cap B)}{\mathbb{P}(B)}\]

Für \(\mathbb{P}(A\cap B)\) im Zähler können wir äquivalent \(\frac{\mathbb{P}(A\cap B)}{\mathbb{P}(A)}\cdot \mathbb{P}(A)\) schreiben. Daraus ergibt sich für die Formel oben:

\[\mathbb{P}(A|B)=\frac{\frac{\mathbb{P}(A\cap B)}{\mathbb{P}(A)}\cdot \mathbb{P}(A)}{\mathbb{P}(B)}\]

Gleichzeitig gilt aber auch:

\[\mathbb{P}(B|A)=\frac{\mathbb{P}(A\cap B)}{\mathbb{P}(A)}\]

Das können wir nun im Zähler ersetzen und erhalten so den Satz von Bayes:

\[\mathbb{P}(A|B)=\frac{\mathbb{P}(B|A)\cdot \mathbb{P}(A)}{\mathbb{P}(B)}\]

7.2.5 Das Gesetz der total Wahrscheinlichkeiten

Wenn wir die Wahrscheinlichkeiten für mehrstufige Zufallsexperimente berechnen wollen müssen wir oft Wahrscheinlichkeiten von verschiedenen Ebenen “aggregieren”. Das machen wir mit dem Gesetz der totalen Wahrscheinlichkeit, das in Beweisen im Bereich der Stochastik sehr häufig verwendet wird. Formal besagt das Gesetz der totalen Wahrscheinlichkeit folgendes: seien \(A_1,...,A_k\) Ergeignisse, die sich nicht überschneiden und gemeinsam den kompletten Ereignisraum \(\Omega\) abdecken, dann gilt:

\[\mathbb{P}(B)=\sum_{i=1}^k\mathbb{P}(B|A_k)\mathbb{P}(A_k)\]

Das sieht natürlich erst einmal sperrig aus, wie so oft ist es aber eigentlich ganz einfach. Das folgende Beispiel illustriert das.

Beispiel für die Anwendung vom Gesetz der totalen Wahrscheinlichkeit: Wir haben eine Urne mit drei weißen und sieben schwarzen Kugeln. Wir ziehen zweimal eine Kugel ohne sie dabei zurückzulegen - wir haben es also mit einem zweistufigen Zufallsexperiment zu tun. Wie hoch ist nun die Wahrscheinlichkeit, dass wir genau eine schwarze Kugel gezogen haben? Sei \(B:\) “Eine schwarze Kugel wird gezogen” und $A: $ “Eine weiße Kugel wird gezogen”. Wir addieren nun die Wahrscheinlichkeiten für aller Ergebnisse, die in Kombination zu unserem Gesamtereignis führen, also die Wahrscheinlichkeit erst eine weiße und dann eine schwarze und die Wahrscheinlichkeit erst eine schwarze und dann eine weiße Kugel zu ziehen:

\[\mathbb{P}(B=1)=\frac{7}{9}\cdot\frac{3}{10} + \frac{3}{9}\cdot\frac{7}{10}=\frac{42}{90}\]

wobei \(\mathbb{P}(B|A)=\frac{7}{9}\cdot\frac{3}{10}\) und \(\mathbb{P}(A|B)=\frac{3}{9}\cdot\frac{7}{10}\). Die Wahrscheinlichkeit genau eine schwarze Kugel zu ziehen liegt also bei ca. \(45.5\) Prozent.

7.3 Diskrete Wahrscheinlichkeitsmodelle

Wenn wir die Wahrscheinlichkeit für das Eintreten eines Ereignisses \(A\) erfahren möchten können wir im Falle eines diskreten Ergebnisraums einfach die Eintrittswahrscheinlichkeiten für alle Ergebnisse, die zu \(A\) gehören, aufsummieren:

\[ \mathbb{P}(A)=\sum_{\omega\in A} \mathbb{P}(\{\omega\})\]

Beispiel: Beim Werfen eines sechseitigen Würfels ist die Wahrscheinlichkeit für das Ereignis “Es wird eine gerade Zahl gewürfelt”: \(\mathbb{P}(2)+\mathbb{P}(4)+\mathbb{P}(6)=\frac{1}{6}+\frac{1}{6}+\frac{1}{6}=\frac{1}{2}\).

7.3.1 Diskrete Zufallsvariablen

Bei Zufallsvariablen (ZV) handelt es sich um besondere Funktionen. Die Definitionsmenge einer Zufallsvariable ist immer der zurgundeliegende Ergebnisraum \(\Omega\), die Zielmenge ist i.d.R. \(\mathbb{R}\), sodass gilt:

\[X:\Omega\rightarrow\mathbb{R}, \omega \mapsto X(\omega)\]

Im Kontext von ZV sprechen wir häufig nicht von dem zugrundeliegenden Ergebnisraum \(\Omega\), sondern - inhaltlich äquivalent - vom Wertebereich von X, bezeichnet als \(W_X\). Produkte und Summen von ZV sind selbst wieder Zufallsvariablen. Man addiert bzw. multipliziert ZV indem man ihre Werte addiert bzw. mutlipliziert.

In der Regel bezeichnen wir Zufallsvariablen mit Großbuchstaben und die konkrete Realisation einer ZV mit einem Kleinbuchstaben, sodass \(\mathbb{P}(X=x)\) die Wahrscheinlichkeit angibt, dass die ZV \(X\) den konkreten Wert \(x\) annimmt. Bei \(x\) sprechen wir von einer Realisierung der ZV \(X\). Wir nehmen für die weitere Notation an, dass \(W_X=\{x_1, x_2,...,x_K\}\) und bezeichnen das einzelne Element mit \(x_k\) mit \(1\leq k\leq K\).

Dies bedeutet streng genommen, dass die ZV selbst nicht als zufällig definiert wird. Zufällig ist nur der Input \(\omega\) der entsprechenden Funktion \(X: \Omega\rightarrow X(\omega)\), also z.B. ein Würfelwurf. Der funktionale Zusammenhang zwischen Funktionswert \(X(\omega)\) und dem Input \(\omega\) ist hingegen eindeutig und deterministisch.

Das impliziert, dass wenn ein Zufallsexperiment zweimal das gleiche Ergebnis \(\omega\) hat, auch der Wert \(X(\omega)\) der gleiche ist.

Das mag im Moment ein wenig nach ‘Pfennigfuchserei’ aussehen, die Unterscheidung zwischen dem nicht-zufälligem funtionalen Zusammenhang, aber einem zufälligen Input bei ZV ist wichtig, um den Sinn in vielen fortgeschrittenen Beiträgen im Bereich der Ökonometrie zu sehen.

Im Falle von diskreten ZV können wir eine Liste erstellen, die für alle möglichen Werte \(x_k\in W_X\) die jeweilige Wahrscheinlichkeit \(\mathbb{P}(X=x_k)\) angibt.⁶⁶ Diese Liste nennen wir Wahrscheinlichkeitsverteilung von \(X\) und sie wird häufig visuell dargestellt. Um diese Liste zu erstellen verwenden wir die zu \(X\) gehörende Wahrscheinlichkeitsfunktion (Probability Mass Function, PMF), \(p(x_k)\), die uns für jedes Ergebnis die zugehörige Wahrscheinlichkeit gibt:⁶⁷

\[p(x_k)=\mathbb{P}(X=x_k)\]

Ebenfalls häufig verwendet wird die kumulierte Wahrscheinlichkeitsfunktion (cumulative distribution function, CDF):

\[F_X(a)=\mathbb{P}(X\leq x_k)\]

Die CDF einer diskrete ZV \(X\) gibt also die Wahrscheinlichkeit an, dass \(X\) sich als ein Wert kleiner gleich einem Schwellenwert realisiert. Daher auch der Name: sie kumuliert die Eintrittswahrscheinlichkeiten aller Events zwischen \(-\infty\) und \(a\). Für eine solche Funktion gilt wie für die PMF, dass \(0\leq F_X(a)\leq1\). Zudem handelt es sich bei der CDF um eine wachsende Funktion (\(F_X(a)\leq F(b) \leftrightarrow a\leq b\)) und es gilt, dass \(\lim_{a\rightarrow \infty}F_X(a)=1\) sowie \(\lim_{a\rightarrow -\infty}F_X(a)=0\), d.h. für sehr große Werte von \(a\) geht \(F_X\) gegen 1 und für sehr kleine Werte gegen 0.

Wenn wir eine ZV analysieren tun wir dies in der Regel durch eine Analyse ihrer Wahrscheinlichkeitsverteilung. Zur genaueren Beschreibung einer ZV wird entsprechend häufig einfach die Wahrscheinlichkeitsfunktion angegeben.

Im Folgenden wollen wir einige häufig auftretende Wahrscheinlichkeitsverteilungen kurz einführen Am Ende des Abschnitts findet sich dann ein tabellarischer Überblick. Doch vorher wollen wir uns noch mit den wichtigsten Kennzahlen einer Verteilung vertraut machen. Denn wie Sie sich vorstellen können sind Wahrscheinlichkeitsverteilungen als Listen, die alle möglichen Realisierungen einer ZV enthalten ziemlich umständlich zu handhaben. Daher beschreiben wir Wahrscheinlichkeitsverteilungen nicht indem wir eine Liste beschreiben, sondern indem wir bestimmte Kennzahlen zu ihrer Beschreibung verwenden. Die wichtigsten Kennzahlen einer ZV \(X\) sind der Erwartungswert \(\mathbb{E}(x)\) als Lageparameter und die Standardabweichung \(\sigma(X)\) als Streuungsmaß.

Der Erwartungswert ist definitert als die nach ihrer Wahrscheinlichkeit gewichtete Summe aller Elemente im Wertebereich von \(X\) und gibt damit die mittlere Lage der Wahrscheinlichkeitsverteilung an. Wenn \(W_X\) der Wertebereich von \(X\) ist, dann gilt:

\[\mathbb{E}(x)=\mu_X=\sum_{x_k\in W_X}p(x_k)x_k\]

Beispiel: Der Erwartungswert einer ZV \(X\), die das Werfen eines fairen Würfels beschreibt ist: \(\mathbb{E}(X)=\sum_{k=1}^6k\cdot\frac{1}{6}=3.5\).

Wie wir im Kapitel 9 sehen werden, wird der Erwartungswert in der empirischen Praxis häufig über den Mittelwert einer Stichprobe identifiziert.

Ein gängiges Maß für die Streuung einer Verteilung \(X\) ist die Varianz \(Var(X)\) oder ihre Quadratwurzel, die Standardabweichung, \(\sigma(X)=\sqrt{Var(X)}\). Letztere wird häufiger verwendet, weil sie die gleiche Einheit hat wie \(X\):

\[Var(X)=\sum_{x_k\in W_X}\left[x_k-\mathbb{E}(X)\right]^2 p(x_k)\]

Beispiel: Die Standardabweichung einer ZV \(X\), die das Werfen eines fairen Würfels beschreibt ist: \(\sigma_X=\sqrt{\sum_{k}^6\left[x_k-\mathbb{E}(X)\right]^2 p(x_k)}=\sqrt{5.83}\approx 2.414\).

Im Folgenden wollen wir uns einige der am häufigsten verwendeten ZV und ihre Verteilungen genauer ansehen. Am Ende der Beschreibung jeder Funktion folgt ein Beispiel für eine Anwendung. Wenn Ihnen die theoretischen Ausführungen am Anfang etwas kryptisch erscheinen, empfiehlt es sich vielleicht erst einmal das Anwendungsbeispiel anzusehen.

7.3.2 Beispiel: die Binomial-Verteilung

Die vielleicht bekannteste diskrete Wahrscheinlichkeitsverteilung ist die Binomialverteilung \(\mathcal{B}(n,p)\). Mit ihr modelliert man Zufallsexperimente, die aus einer Reihe von Aktionen bestehen, die entweder zum ‘Erfolg’ oder ‘Misserfolg’ führen.

Die Binomialverteilung ist eine Verteilung mit zwei Parametern. Parameter sind Werte, welche die Struktur der Verteilung bestimmen. In der Statistik sind wir häufig daran interessiert, die Paramter einer Verteilung zu bestimmen. Im Falle der Binomialverteilung gibt es die folgenden zwei Parameter: \(p\) gibt die Erfolgswahrscheinlichkeit einer einzelnen Aktion an (und es muss daher gelten \(p\in[0,1]\)) und \(n\) gibt die Anzahl der Aktionen an. Daher auch die Kurzschreibweise \(\mathcal{B}(n,p)\).

Beispiel: Wenn wir eine faire Münze zehn Mal werfen, können wir das mit einer Binomialverteilung mit \(p=0.5\) und \(n=10\) modellieren.

Die Wahrscheinlichkeitsfunktion \(p(x)\) der Binomialverteilung ist die Folgende, wobei \(x\) die Anzahl der Erfolge darstellt:

\[\mathbb{P}(X=x)=p(x)=\binom{n}{x}p^x(1-p)^{n-x}\] Dies ergibt sich aus den grundlegenden Wahrscheinlichkeitsgesetzen: \(\binom{n}{x}\) ist der Binomialkoeffizient und gibt uns die Anzahl der Möglichkeiten wie man bei \(n\) Versuchen \(x\) Erfolge erzielen kann. Dies multiplizieren wir mit der Wahrscheinlichkeit \(x\)-mal einen Erfolg zu erzielen und \(n-x\)-mal einen Misserfolg zu erzielen.

Wenn die ZV \(X\) einer Binomialverteilung mit bestimmten Parametern \(p\) und \(n\) folgt, dann schreiben wir \(P \propto \mathcal{B}(n,p)\) und es gilt, dass \(\mathbb{E}(X)=np\) und \(\sigma(X)=\sqrt{np(1-p)}\).⁶⁸

In Abbildung 7.1 sehen wir eine Darstellung der Wahrscheinlichkeitsverteilung der Binomialverteilung für verschiedene Parameterwerte.

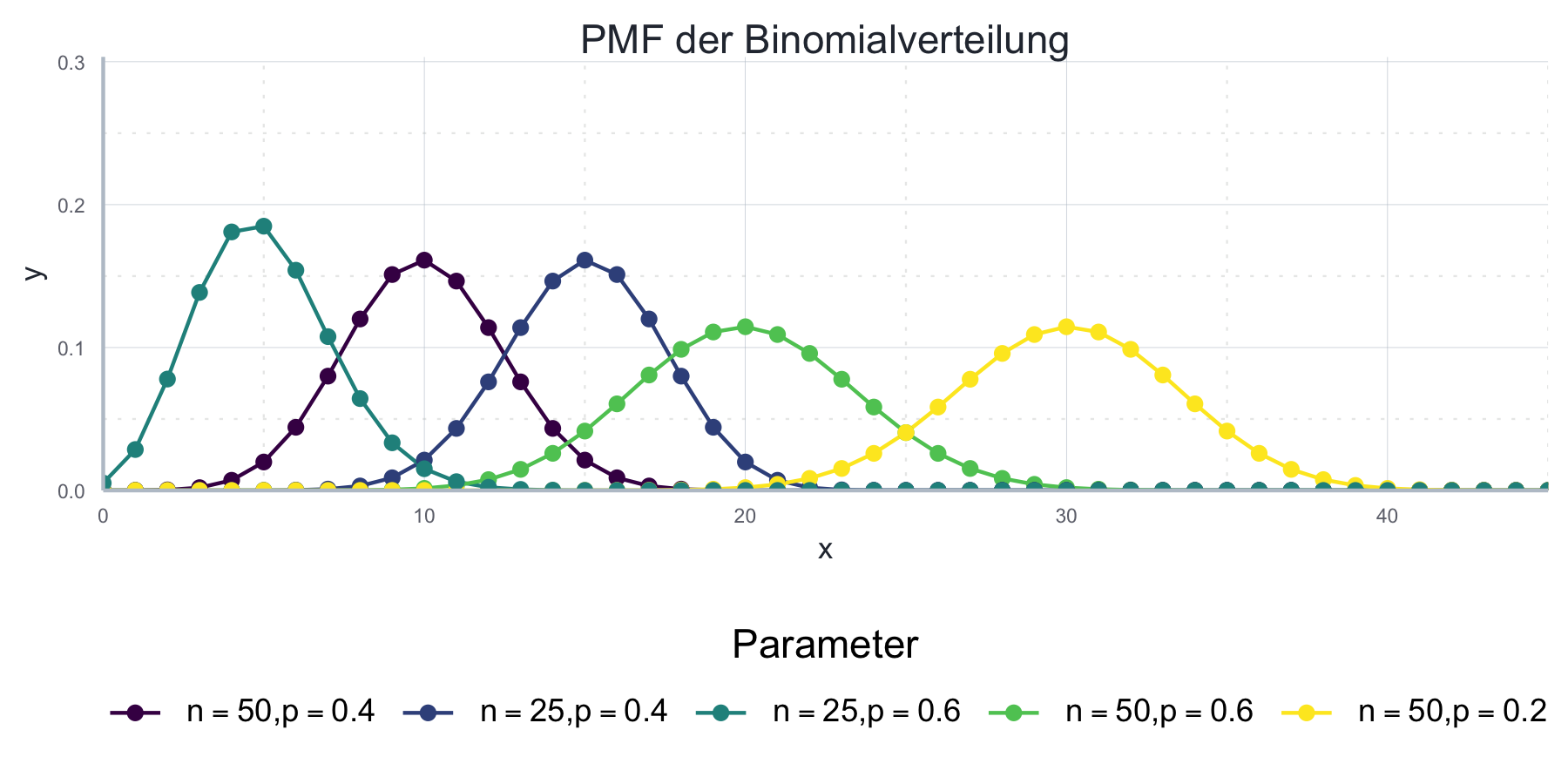
Abbildung 7.1: Die Wahrscheinlichkeitsverteilung der Binomialverteilung für verschiedene Parameterwerte.

R stellt uns einige nützliche Funktionen bereit, mit denen wir typische Rechenaufgaben einfach lösen können:

Möchten wir die Wahrscheinlichkeit berechnen, genau \(x\) Erfolge zu beobachten, also \(\mathbb{P}(X=x)\) geht das mit der Funktion dbinom(). Die notwendigen Argumente sind x für den interessierenden x-Wert, size für den Parameter \(n\) und prob für den Parameter \(p\):

dbinom(x = 10, size = 50, prob = 0.25)

#> [1] 0.09851841

Das bedeutet, wenn \(X \propto B(50, 0.25)\), dann: \(\mathbb{P}(X=10)=0.09852\). Dies ist in Abbildung 7.2 illustriert.

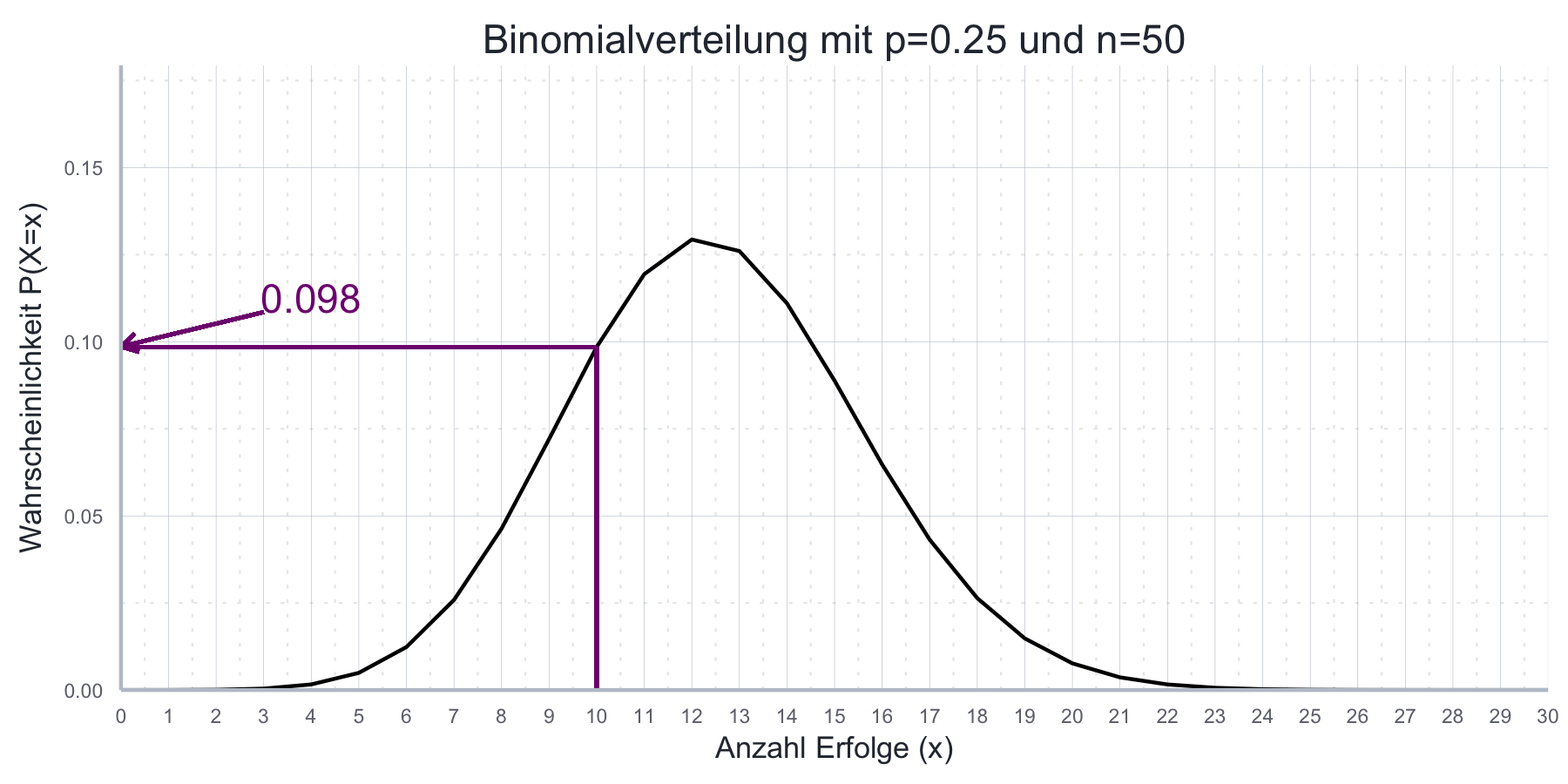
Abbildung 7.2: Beispiel einer Binomialverteilung mit \(p\)=0.25 und \(n\)=50.

Natürlich können wir an die Funktion auch einen atomaren Vektor als erstes Argument übergeben:

dbinom(x = 5:10, size = 50, prob = 0.25)

#> [1] 0.004937859 0.012344647 0.025864974 0.046341412 0.072086641 0.098518410

Häufig sind wir auch an der kumulierten Wahrscheinlichkeitsfunktion interessiert. Während uns die Wahrscheinlichkeitsfunktion die Wahrscheinlichkeit für genau \(x\) Erfolge angibt, also \(\mathbb{P}(X=x)\), gibt uns die kumulierte Wahrscheinlichkeitsfunktion die Wahrscheinlichkeit für \(x\) oder weniger Erfolge, also \(\mathbb{P}(X\leq x)\).

Die entsprechenden Werte für die kumulierten Wahrscheinlichkeitsfunktion erhalten wir mit der Funktion pbinom(), welche quasi die gleichen Argumente benötigt wie dbinom(). Nur gibt es anstatt des Parameters x jetzt einen Parameter q:

pbinom(q = 10, size = 50, prob = 0.25)

#> [1] 0.2622023

Die Wahrscheinlichkeit 10 oder weniger Erfolge bei 10 Versuchen und einer Erfolgswahrscheinlichkeit von 25% zu erzielen beträgt also 26.2%. Dies ist auch in Abbildung 7.3 ersichtlich.

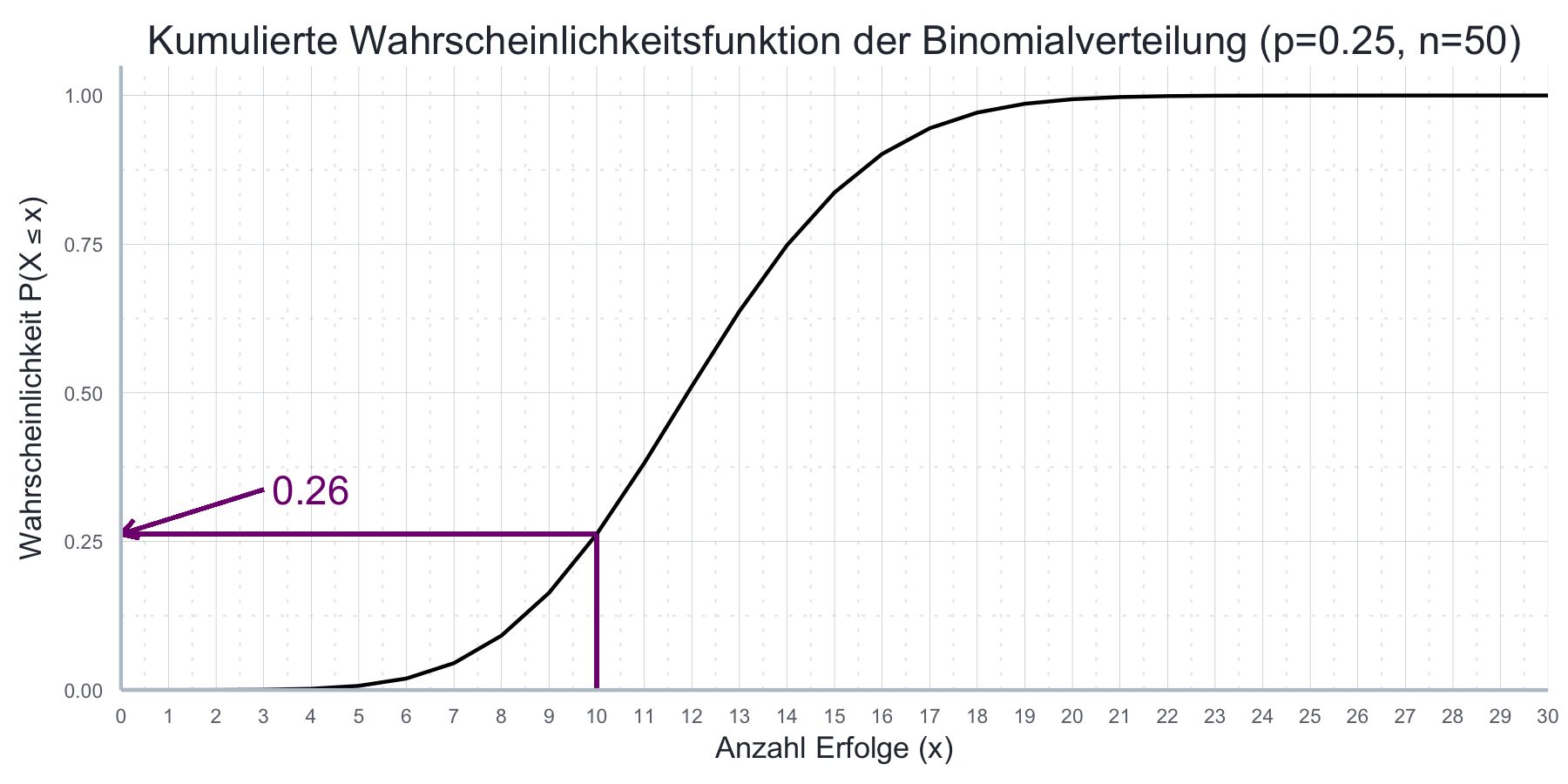
Abbildung 7.3: Kumulative Wahrscheinlichkeitsfunktion mit \(p\)=0.25 und \(n\)=50

Schlussendlich haben wir die Funktion qbinom(), welche als ersten Input eine Wahrscheinlichkeit p akzeptiert und dann den kleinsten Wert \(x\) findet, für den gilt, dass \(\mathbb{P}(X=x)\geq p\).

Wenn wir also wissen möchten wie viele Erfolge mit einer Wahrscheinlichkeit von 50% mindestens zu erwarten sind, dann schreiben wir:

qbinom(p = 0.5, size = 50, prob = 0.25)

#> [1] 12

Es gilt also: \(\mathbb{P}(X=12)\geq p\).

Abbildung 7.4 verdeutlicht dies grafisch.

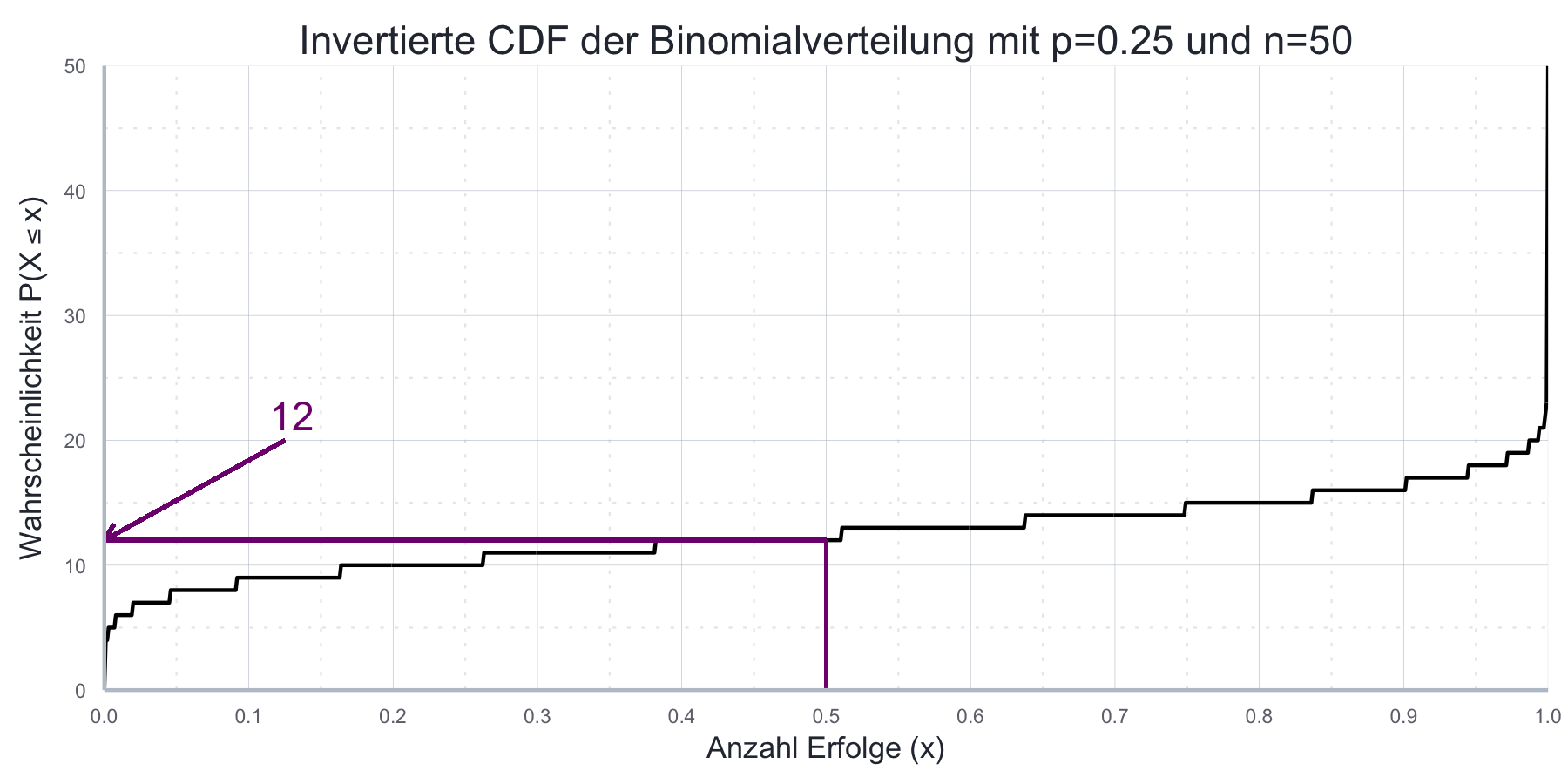
Abbildung 7.4: Graph der invertierten kumulierten Wahrscheinlichkeitsfunktion der Binomialverteilung mit \(p=0.25\) und \(n=50\)

Möchten wir schließlich eine bestimmte Menge an Realisierungen aus einer Binomialverteilung ziehen geht das mit der Funktion rbinom(), welche auch wieder drei Argumente verlangt: n für die Anzahl der zu ziehenden Realisierungen, sowie size und prob als da Paramter \(n\) und \(p\) der Binomialverteilung:

sample_binom <- rbinom(n = 5, size = 10, prob = 0.4)
sample_binom

#> [1] 4 3 3 5 4

Anwendungsbeispiel Binomialverteilung: Unser Zufallsexperiment besteht aus dem zehnmaligen Werfen einer fairen Münze. Unter ‘Erfolg’ verstehen wir das Werfen von ‘Zahl’. Nehmen wir an, wir führen das Zufallsexperiment 10 Mal durch, werfen also insgesamt 100 Mal die Münze und schreiben jeweils auf, wie häufig wir dabei einen Erfolg verbuchen konnten. Wenn wir unsere Ergebnisse aufmalen, indem wir auf der x-Achse die Anzahl der Erfolge, und auf der y-Achse die Anzahl der Experimente mit genau dieser Anzahl an Erfolgen festhalten, erhalten wir ein Histogram, das ungefähr so aussieht wie in Abbildung 7.5.

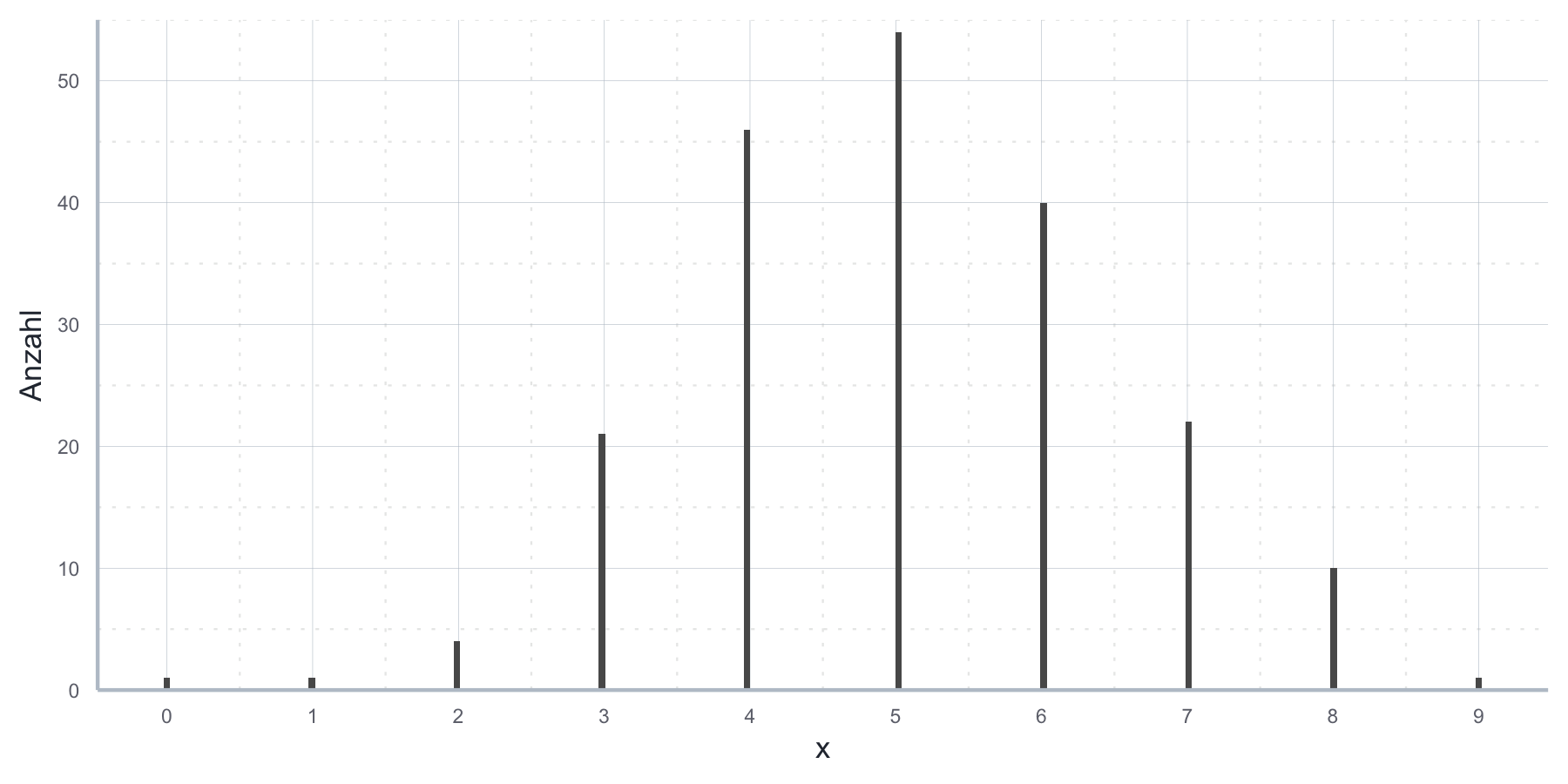
Abbildung 7.5: Histogram für einen Münzwurf.

Aus der Logik der Konstruktion des Zufallsexperiments und der Inspektion unserer Daten können wir schließen, dass die Binomialverteilung eine sinnvolle Beschreibung des Zufallsexperiments und der daraus entstandenen Stichprobe von 100 Münzwurfergebnissen ist. Da wir eine faire Münze geworfen haben macht es Sinn für die Binomialverteilung \(p=0.5\) anzunehmen, und da wir in jedem einzelnen Experiment die Münze 10 Mal geworfen haben für \(n=10\). Wenn wir die mit \(n=10\) und \(p=0.5\) parametrisierte theoretische Binomialverteilung nehmen und ihre theoretische Verteilungsfunktion über die Aufzeichnungen unserer Ergebnisse legen, können wir uns in dieser Vermutung bestärkt fühlen, wie in Abbildung 7.6 ersichtlich ist.

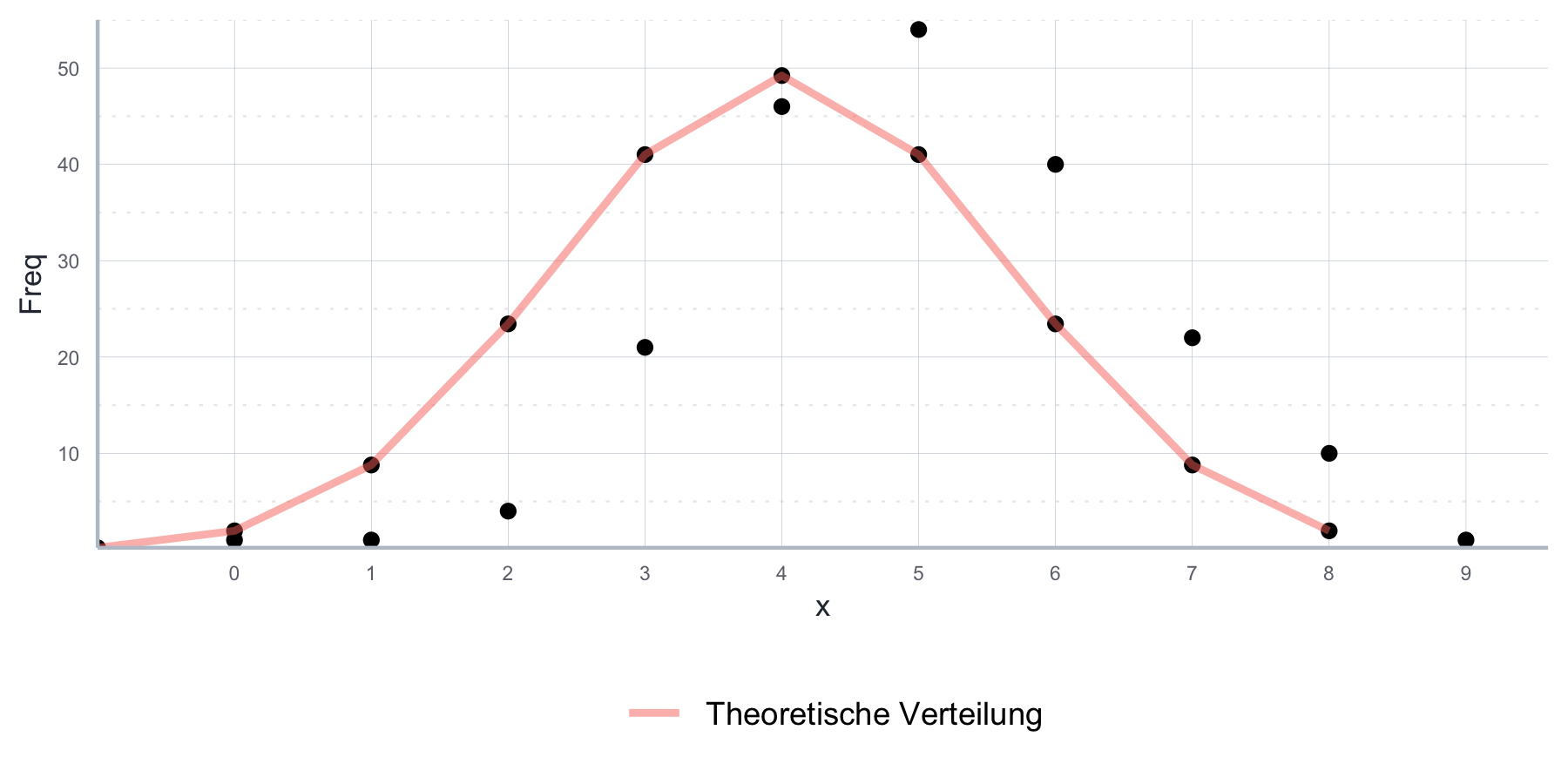
Abbildung 7.6: Vergleich der empirischen Stichprobe und der parametrisierten theoretischen Binomialverteilungsfunktion

7.3.3 Beispiel: die Poisson-Verteilung

Bei der Poisson-Verteilung handelt es sich um die Standardverteilung für unbeschränkte Zähldaten, also diskrete Daten, die kein natürliches Maximum haben.

Es handelt sich dabei zudem um eine ein-parametrische Funktion, deren einziger Parameter \(\lambda>0\) ist. \(\lambda\) wird häufig als die mittlere Ereignishäufigkeit interpretiert und ist zugleich Erwartungswert als auch Varianz der Verteilung: \(\mathbb{E}(P_\lambda)=Var(P_\lambda)=\lambda\).

Ihre Definitionsmenge ist \(\mathbb{N}\), also alle natürlichen Zahlen - daher ist sie im Gegensatz zur Binomialverteilung geeignet, wenn die Definitionsmenge der Verteilung keine natürliche Grenze hat.

Die Wahrscheinlichkeitsfunktion der Poisson-Verteilung hat die folgende Form:

\[p_\lambda(x)=\frac{\lambda^x}{x!}e^{-\lambda}\] Abbildung 7.7 zeigt wie sich die Wahrscheinlichkeitsfunktion für unterschiedliche Werte von \(\lambda\) manifestiert.

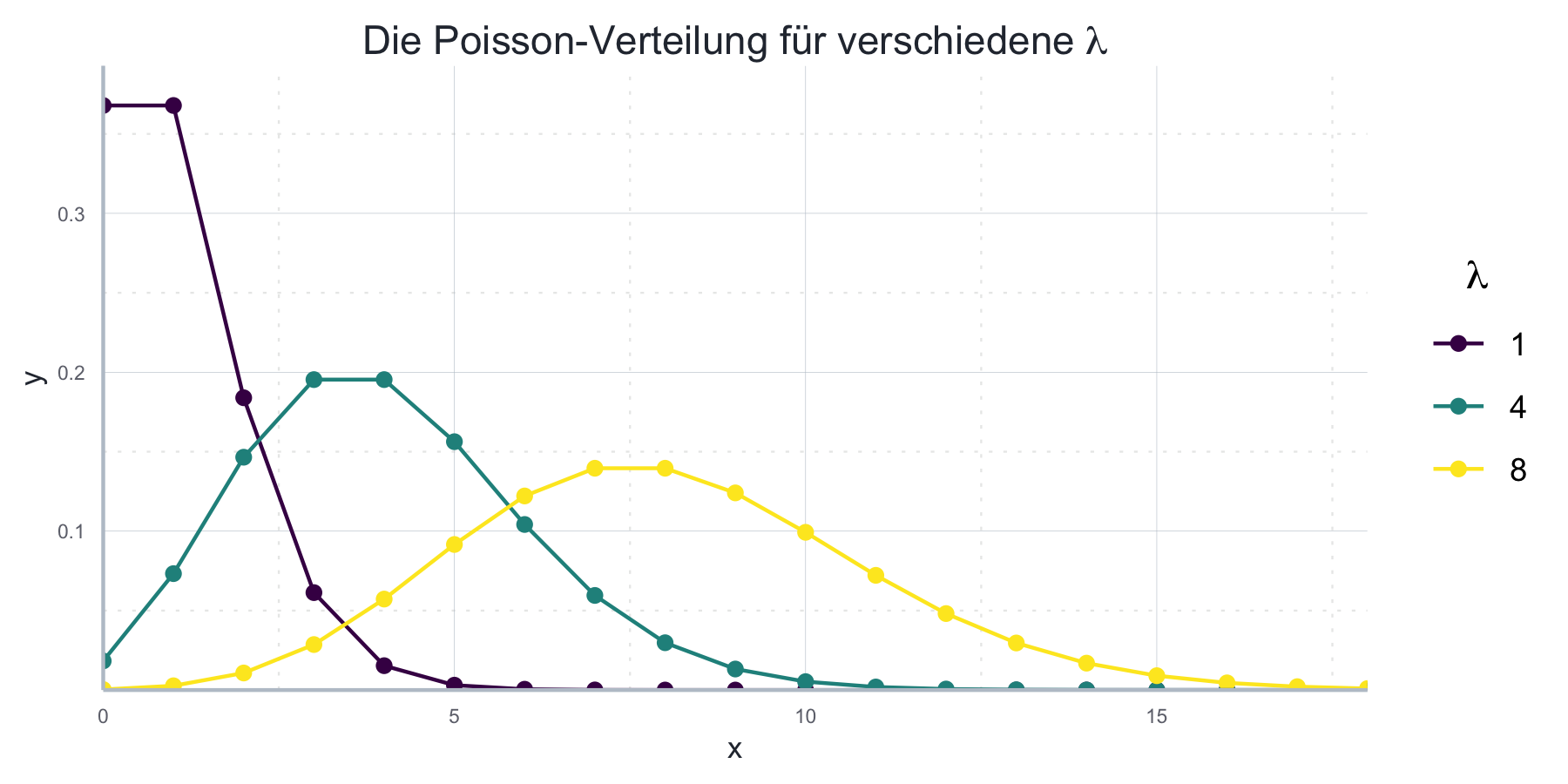
Abbildung 7.7: Poisson-Verteilung für verschiedene Parameter.

Wir können die Verteilung mit sehr ähnlichen Funktionen wie bei der Binomialverteilung analysieren. Nur die Parameter müssen entsprechend angepasst werden, da es bei der Poisson-Verteilung jetzt nur noch einen Paramter (lambda) gibt.

Möchten wir die Wahrscheinlichkeit berechnen, genau \(x\) Erfolge zu beobachten, also \(\mathbb{P}(X=x)\) geht das mit der Funktion dpois(). Das einzige notwendige Argument ist lambda (siehe zudem Abbildung 7.8):

dpois(5, lambda = 4)

#> [1] 0.1562935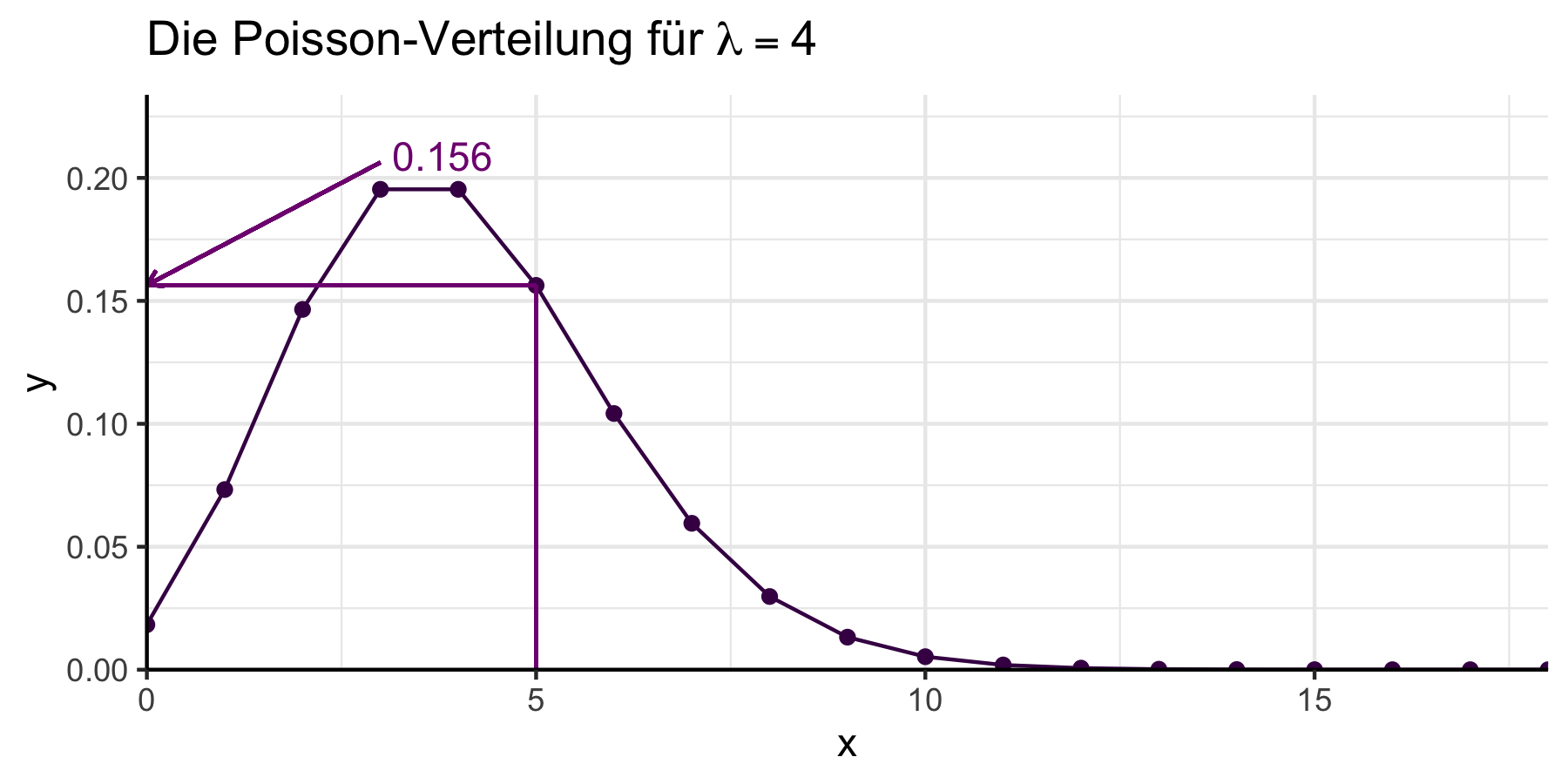

Abbildung 7.8: Poisson-Verteilung mit ausgewählten Parameterwerten.

Informationen über die CDF erhalten wir über die Funktion ppois(), die zwei Argumente, q und lambda, annimmt. Grafisch dargestellt ist dies in Abbildung 7.9.

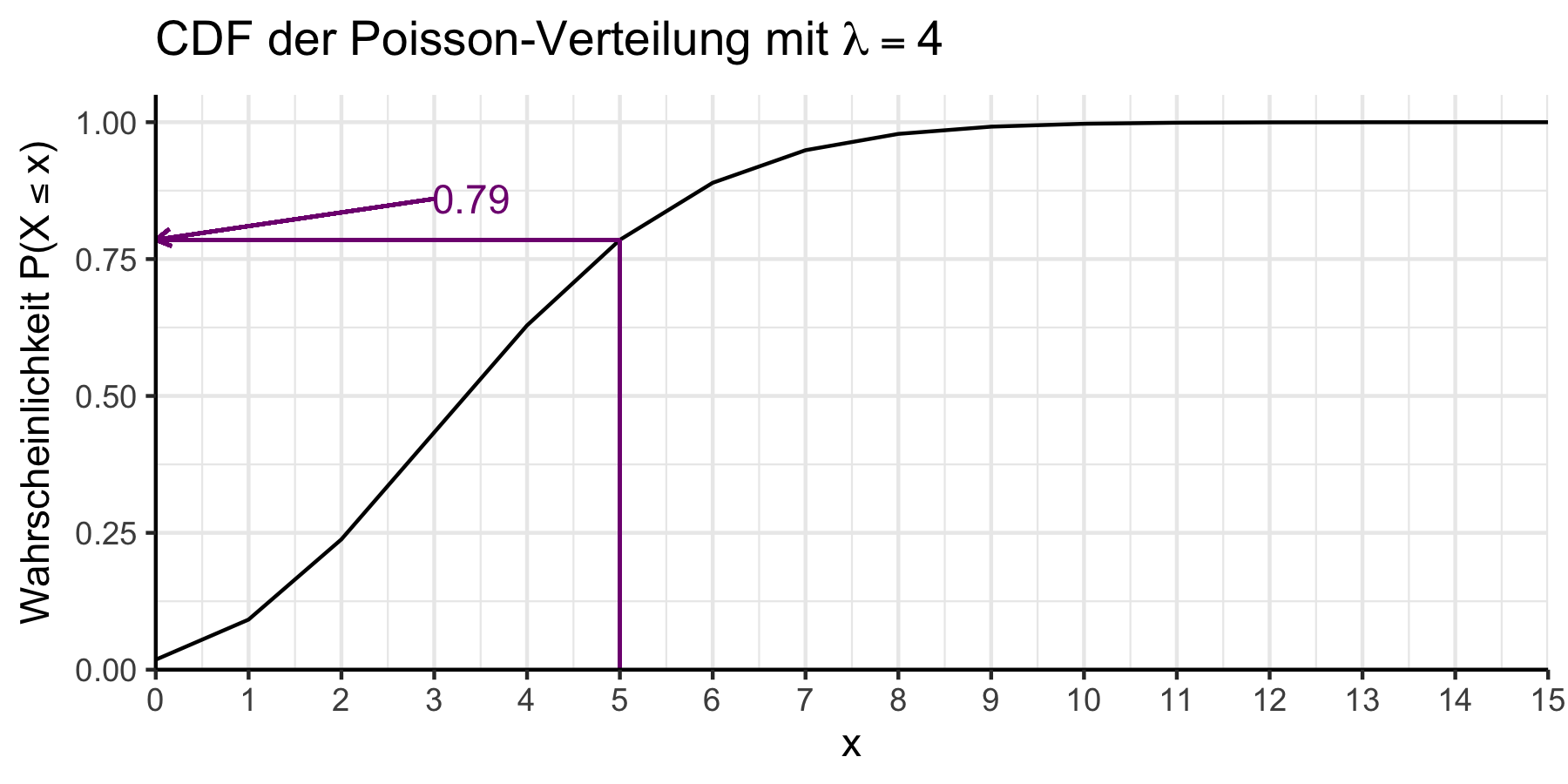
Abbildung 7.9: Kumulierte Wahrscheinlichkeitsfunktion der Poisson-Verteilung mit \(\lambda = 4\)

Mit der Funktion qpois() finden wir für eine Wahrscheinlichkeit p den kleinsten Wert \(x\), für den gilt, dass \(\mathbb{P}(X=x)\geq p\).

Wenn wir also wissen möchten wie viele Erfolge mit einer Wahrscheinlichkeit von 50% mindestens zu erwarten sind, dann schreiben wir:

qpois(p = 0.5, lambda = 4)

#> [1] 4

Es gilt also: \(\mathbb{P}(X=4)\geq 0.5\).

Wir können dies erneut grafisch verdeutlichen, wie in Abbildung 7.10 dargestellt.

Abbildung 7.10: Invertierte CDF der Poisson-Verteilung mit \(\lambda = 4\)

Möchten wir schließlich eine bestimmte Menge an Realisierungen der ZV aus einer Poisson-Verteilung ziehen geht das mit rpois(), welches zwei notwendige Argumente annimmt: n für die Anzahl der Realisierungen und lambda für den Parameter \(\lambda\):

pois_sample <- rpois(n = 5, lambda = 4)
pois_sample

#> [1] 3 8 4 4 3

7.3.4 Hinweise zu diskreten Wahrscheinlichkeitsverteilungen

Wie Sie vielleicht bereits bemerkt haben sind die R Befehle für verschiedene Verteilungen alle gleich aufgebaut. Wenn * für die Abkürzung einer bestimmten Verteilung steht, können wir mit der Funktion d*() die Werte der Wahrscheinlichkeitsverteilung, mit p*() die Werte der kumulierten Wahrscheinlichkeitsverteilung und mit q*() die der Quantilsfunktion berechnen. Mit r*() werden Realisierungen von Zufallszahlen generiert. Für das Beispiel der Binomialverteilung, welcher die Abkürzung binom zugewiesen wurde, heißen die Funktionen entsprechend dbinom(), pbinom(), qbinom() und rbinom().

Tabelle 7.2 gibt einen Überblick über gängige Abkürzungen und die Parameter der oben besprochenen diskreten Verteilungen.

Tabelle 7.2: Überblick der besprochenen diskreten Verteilungen.

Verteilung	Abkürzung	Parameter
Binomialverteilung	binom	size, prob
Poisson-Verteilung	pois	lambda

7.4 Stetige Wahrscheinlichkeitsmodelle

7.4.1 Stetige ZV

In vorangegangen Abschnitt haben wir uns mit diskreten Wahrscheinlichkeitsmodellen beschäftigt. Die diesen Modellen zugrundeliegenden ZV hatten einen abzählbaren Wertebereich. Häufig interessieren wir uns aber für ZV mit einem nicht abzählbaren Wertebereich, z.B. \(\mathbb{R}\) oder \([0,1]\).⁶⁹

Bei stetigen Wahrscheinlichkeitsmodellen liegen zwischen zwei Punkten unendlich viele Punkte. Das hat bedeutende Implikationen für die Angabe von Wahrscheinlichkeiten. Im Gegensatz zu diskreten Wahrscheinlichkeitsmodellen hat demnach jeder einzelne Punkt im Wertebereich der ZV die Wahrscheinlichkeit 0:

\[\mathbb{P}(X=x_k)=0 \quad \forall x_k \in W_X\] wobei \(W_X\) für den Wertebereich von ZV \(X\) steht.

Als Lösung werden Wahrscheinlichkeiten bei stetigen ZV nicht als Punktwahrscheinlichkeiten, sondern als Intervallwahrscheinlichkeiten angeben. Aus \(\mathbb{P}(X=x)\) im diskreten Fall wird im stetigen Fall also:

\[\begin{align} \mathbb{P}(a<X\leq b) = \int_a^bf(x)dx, \quad a<b \end{align}\]

Entsprechend wird für stetige ZV eine etwas andere Notation als für diskrete ZV verwendet, wobei das Prinzip gleich bleibt. Zudem werden Sie merken, dass im stetigen Fall anstatt Summen immer Integrale verwendet werden. Informell kann man ja auch sagen, dass ein Integral nichts anderes ist als eine Summe über stetige Werte.

Wo wir bei diskreten ZV eine Wahrscheinlichkeitsfunktion (PMF) verwendet haben verwenden wir nun eine Wahrscheinlichkeitsdichte (probability density function, PDF). Aus der PMF \(p_X(x)=\mathbb{P}(X=x_k)\) im diskreten Fall wird nun also die PDF \(f_X(x)\), für die gilt, dass \(\mathbb{P}(a<X\leq b) = \int_a^bf(x)dx\) für den stetigen Fall.

Für die PDF gilt äquivalent zum diskreten Fall, dass \(f_X(x)\geq0\) (keine negativen Werte) und \(\int_{-\infty}^{\infty}f(x)dx=1\) (das Integral (die ‘stetige Summe’) über den ganzen Wertebereich ergibt 1). Allerdings gibt es einen wichtigen Unterschied: im Gegensatz zur PMF \(p_X(x)\) gibt die PDF \(f_X(x)\) keine Wahrscheinlichkeiten an - daher auch nur die Restriktion \(f_X(x)\geq0\) und nicht \(1\geq f_X(x)\geq0\). Wenn wir von Wahrscheinlichkeiten reden wollen, müssen wir die PDF integrieren:

\[\mathbb{P}((a,b])=\int_a^bf(x)dx\]

da wir im stetigen Fall für einzelne Punkte keine von Null verschiedenen Wahrscheinlichkeiten haben.

Wen übrigens die unterschiedlichen Bezeichnungen “probability mass” und “probablity density” irritieren: tatsächlich ist die Verwendung dieser Bezeichnungen ganz analog zu den physikalischen Pendents “Masse” und “Dichte” in der Physik: wenn wir die Masse für einzelne Teile einer Stange haben bekommen wir die Gesamtmasse indem wir die Masse der Teile addieren - das ist genauso wie bei der PMF: wir bekommen die Gesamtwahrscheinlichkeit indem wir die Wahrscheinlichkeiten für einzelne Events addieren und die Einzelgewichte indem wir uns die Masse der einzelnen Teile ansehen. Wenn wir jetzt eine Stange haben, die unterschiedlich dicht ist, bekommen wir die gesamte Masse indem wir über die Dichte integrieren. Wir können die Stange auch in kleinere Teile schneiden und deren Masse addieren. Wenn die Teile unendlich klein werden kommen wir zum gleichen Ergebnis wie bei der Integration.

Die kumulative Verteilungsfunktion (CDF) ist im stetigen Fall genauso definiert wie im diskreten Fall: \(F_X(x)=\mathbb{P}(X\leq x)\), wobei immer gilt:

\[\mathbb{P}(a<X\leq b) = F(b)-F(a)=\int_a^bf(x)dx\]

Man sieht hier, dass die Dichtefunktion (PDF) einer ZV die Ableitung ihrer kumulative Verteilungsfunktion (CDF) ist:

\[F_X'(x)=f_X(x)\]

Wie oben beschrieben können wir die Werte an einzelnen Punkten der PDF nicht als absolute Wahrscheinlichkeiten interpretieren, da die Wahrscheinlichkeit für einzelne Punkte immer gleich 0 ist und die PDF auch Werte größer 1 annehmen kann. Wir können aber die Werte der PDF an zwei oder mehr Punkten vergleichen um die relative Wahrscheinlichkeit der einzelnen Punkte zu bekommen.

Wie bei den diskreten ZV beschreiben wir eine ZV mit Hilfe von bestimmten Kennzahlen, wie dem Erwartungswert, der Varianz und den Quantilen. Diese sind quasi äquivalent zum diskreten Fall definiert, nur eben über Integrale (wir vergleichen alle folgenden Definitionen mit ihrem diskreten Pendant am Ende des Abschnitts). Für den Erwartungswert der ZV \(X\) gilt somit:

\[\mathbb{E}(X)=\int_{-\infty}^{\infty}xf(x)dx\]

Für die Varianz und die Standardabweichung entsprechend:

\[Var(X)= \mathbb{E}(X-\mathbb{E}\left(X)\right)^2=\int_{-\infty}^{\infty}(x-\mathbb{E}(X))^2f(x)dx\]

\[\sigma_X=\sqrt{Var(X)}\]

Und, schlussendlich, gilt für das \(\alpha\)-Quantil \(q(\alpha)\):

\[\mathbb{P}(X\leq q(\alpha))=\alpha\]

In Abbildung 7.11 werden das \(0.25\) und \(0.5\)-Quantil visuell dargestellt.

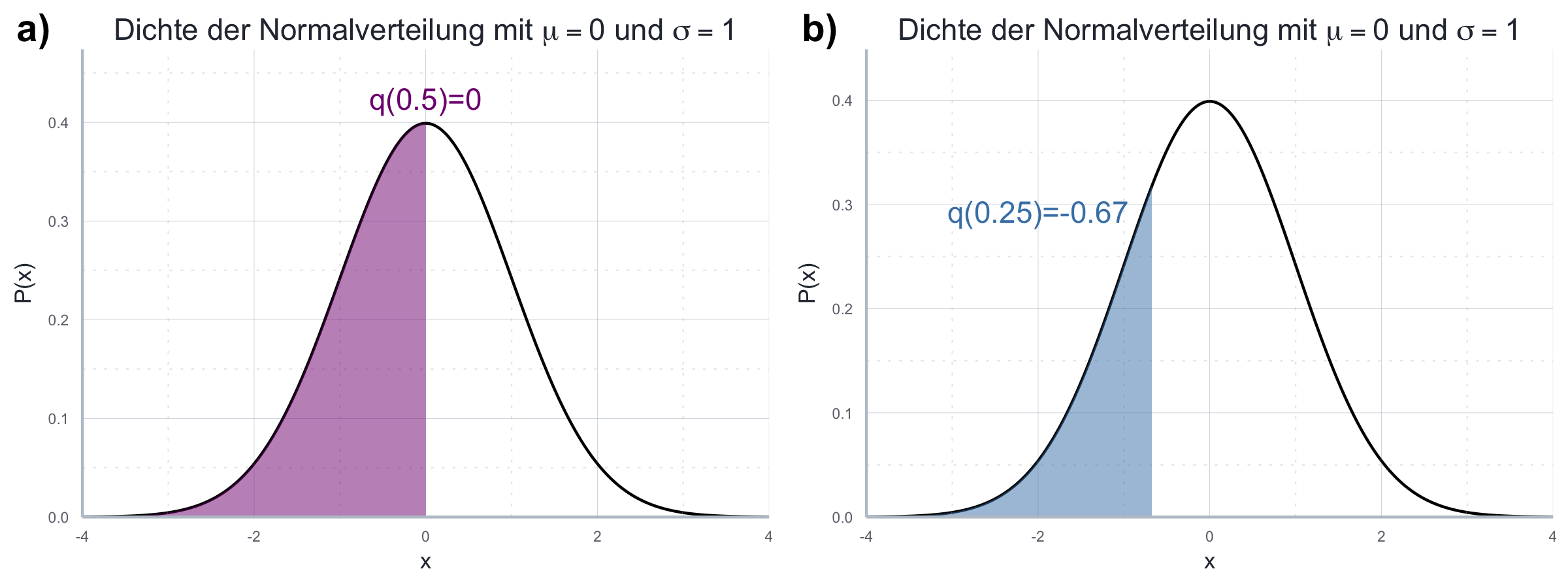
Abbildung 7.11: Vergleich des \(0.25\)- und \(0.5\)-Quantils

Tabelle 7.3 vergleicht noch einmal die Definitionen der Kennzahlen und charakteristischer Verteilungen für den stetigen und diskreten Fall.

Tabelle 7.3: Vergleich der Kennzahlen charakteristischer Verteilungen im stetigen und im diskreten Fall.

Bezeichnung	Diskreter Fall	Stetiger Fall
Erwartungswert	\(\mathbb{E}(x)=\sum_{x\in W_X}\mathbb{P}(X=x)x\)	\(\mathbb{E}(X)=\int_{-\infty}^{\infty}xf(x)dx\)
Varianz	\(Var(X)=\sum_{x\in W_X}\left[x-\mathbb{E}(X)\right]^2 \mathbb{P}(X=x)x\)	\(Var(X)= \mathbb{E}(X-\mathbb{E}\left(X)\right)^2\)
Standard-abweichung	\(\sqrt{Var(X)}\)	\(\sqrt{Var(X)}\)
\(\alpha\)-Quantil	\(\mathbb{P}(X\leq q(\alpha))=\alpha\)	\(\mathbb{P}(X\leq q(\alpha))=\alpha\)
Dichtefunktion (PDF)	NA	\(f_X(x)=\mathbb{P}([a,b])=\int_a^bf(x)dx\)
Wahrsch’s-funktion (PMF)	\(p_X(x_k)=\mathbb{P}(X=x_k)\)	NA
Kumulierte Verteilungsfunktion (CDF)	\(\mathbb{P}(X\leq x)\)	\(F(x)=\mathbb{P}(X\leq x)\)

Analog zum diskreten Fall wollen wir uns nun die am häufigsten vorkommenden stetigen Verteilungen noch einmal genauer anschauen. Vorher wollen wir jedoch die oben eingeführten Konzepte (statistische Unabhängigkeit, bedingte Wahrscheinlichkeiten, etc.) noch für den stegigen Fall formulieren - am Prinzip ändert sich hier nichts, nur an der Notation.

7.4.2 Beispiel: die Uniformverteilung

Die Uniformverteilung kann auch mit einem beliebigen Intervall \([a,b]\) mit \(a<b\) definiert werden und ist dadurch gekennzeichnet, dass die Dichte über \([a,b]\) vollkommen konstant ist. Ihre einzigen Parameter sind die Grenzen des Intervalls, \(a\) und \(b\).

Da bei stetigen Verteilungen die Dichte aller Werte außerhalb des Wertebereichs per definitionem gleich Null ist, haben wir folgenden Ausdruck für die Dichte der Uniformverteilung:

\[f(x)= \begin{cases} \frac{1}{b-a} & a\leq x \leq b \\ 0 & \text{sonst} \left(x\notin W_X\right) \end{cases} \] Auch der Erwartungswert ist dann intuitiv definiert, er liegt nämlich genau in der Mitte des Intervalls \([a,b]\) und ist definiert als \(\mathbb{E}(X)=\frac{a+b}{2}\). Die Varianz ist mit \(Var(X)=\frac{(b-a)^2}{12}\) gegeben.

Die Dichtefunktion der Uniformverteilung für \([a,b]=[2,4]\) ist in Abbildung 7.12 dargestellt:

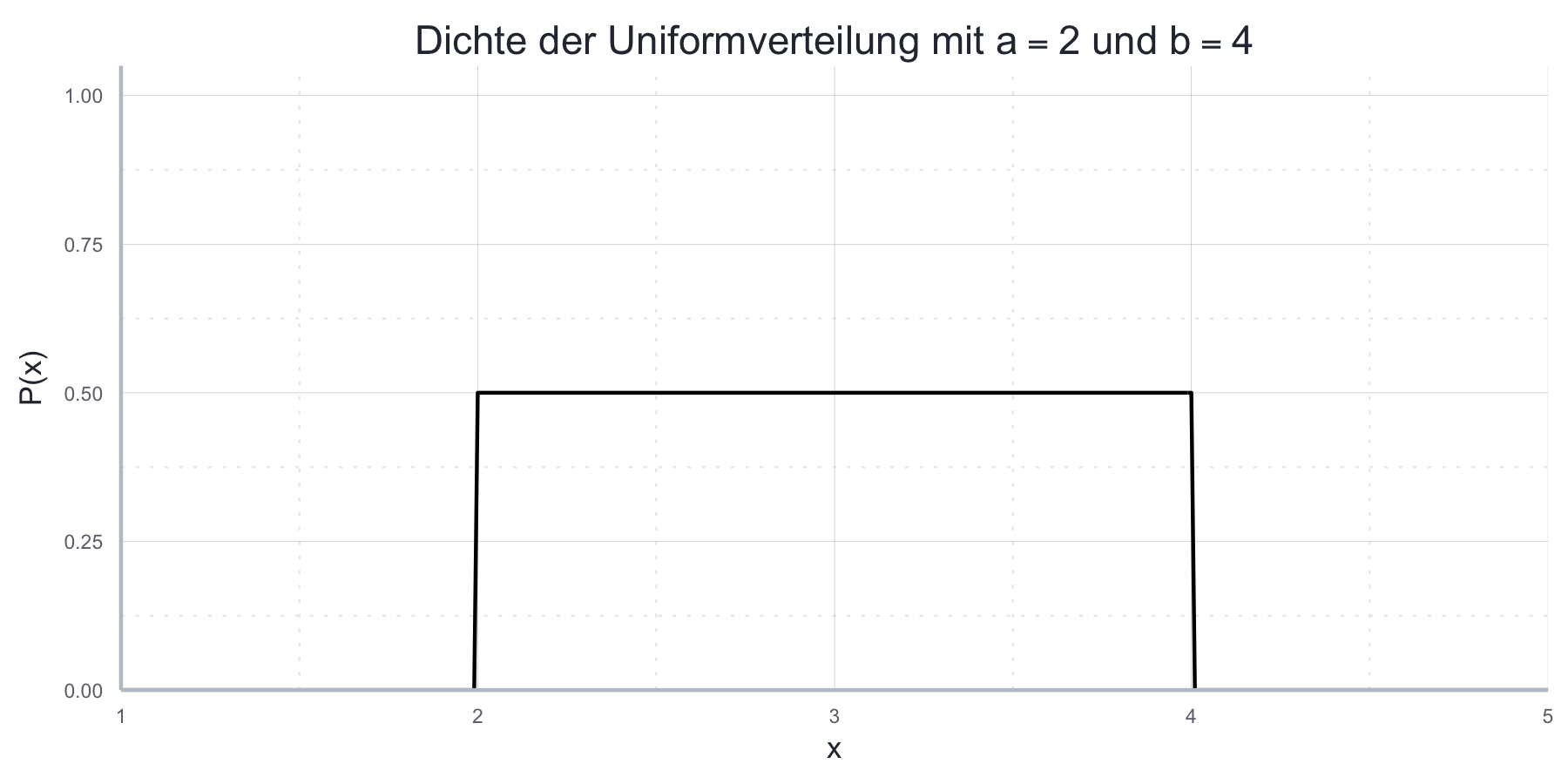
Abbildung 7.12: Dichte der Uniformverteilung mit \(a = 2\) und \(b = 4\)

Die Abkürung in R für die Uniformverteilung ist unif. Endsprechend berechnen wir Werte für die Dichte mit dunif(), welches lediglich die Argumente a und b für die Grenzen des Intervalls benötigt:

dunif(seq(2, 3, 0.1), min = 0, max = 4)

#>  [1] 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25

Wie wir sehen erhalten wir hier immer den gleichen Wert \(\frac{1}{b-a}\), was die zentrale Eigenschaft der Uniformverteilung ist. Hier wird auch deutlich, dass dieser Wert die relative Wahrscheinlichkeit angibt, da die absolute Wahrscheinlichkeit für jeden einzelnen Wert wie oben beschrieben bei stetigen ZV 0 ist.

Die CDF berechnen wir entsprechend mit punif(). Wenn \(X\propto U(0,4)\) erhalten wir \(\mathbb{P}(X\leq3)\) entprechend mit:

punif(0.8, min = 0, max = 4)

#> [1] 0.2

Abbildung 7.13 zeigt dies grafisch.

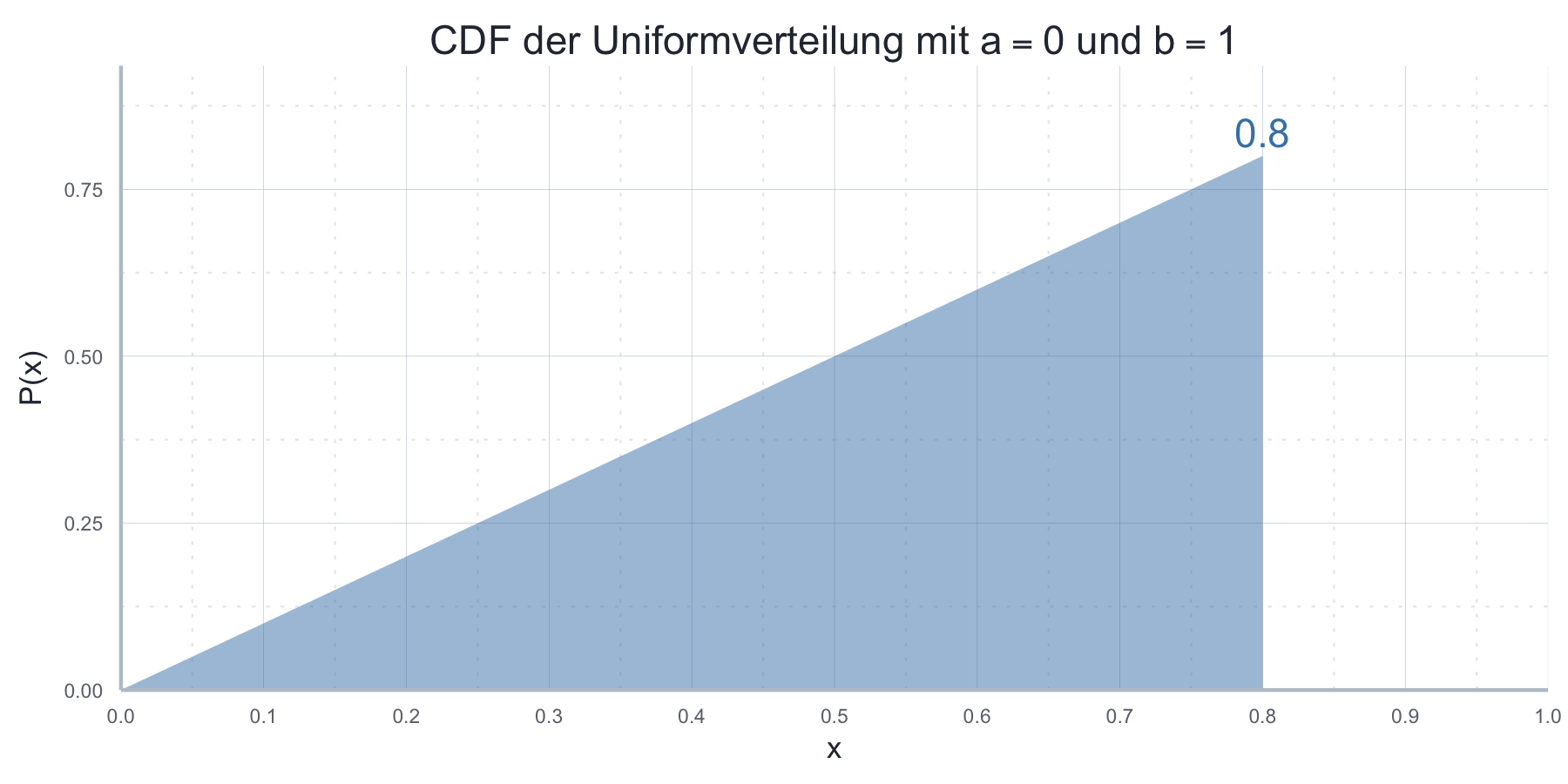
Abbildung 7.13: CDF der Uniformverteilung mit \(a = 0\) und \(b = 1\)

Auch ansonsten können wir die Syntax der diskreten Verteilungen mehr oder weniger übernehmen: qunif() akzeptiert die gleichen Parameter wie punif() und gibt uns Werte der inversen CDF. runif() kann verwendet werden um Realisierungen einer uniform verteilten ZV zu generieren:

uniform_sample <- runif(5, min = 0, max = 4)
uniform_sample

#> [1] 3.5209862 1.4563675 1.1529571 0.6825809 0.6886870

7.4.3 Beispiel: die Normalverteilung

Die wahrscheinlich bekannteste stetige Verteilung ist die Normalverteilung. Das liegt nicht nur daran, dass viele natürliche Phänomene als die Realisierung einer normalverteilten ZV modelliert werden können, sondern auch weil es sich mit der Normalverteilung in der Regel sehr einfach rechnen lässt. Sie ist also häufig auch einfach eine bequeme Annahme.

Bei der Normalverteilung handelt es sich um eine zwei-parametrige Verteilung über den Wertebereich \(W_X=\mathbb{R}\). Die beiden Parameter sind \(\mu\) und \(\sigma^2\), welche unmittelbar als Erwartungswert (\(\mathbb{E}(X)=\mu\)) und Varianz (\(Var(X)=\sigma^2\)) gelten. Wir schreiben \(X\propto \mathscr{N}(\mu, \sigma^2)\) wenn für die PDF von \(X\) gilt:

\[f(x)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]

Unter der Standard-Normalverteilung verstehen wir eine Normalverteilung mit den Paramtern \(\mu=0\) und \(\sigma=1\).⁷⁰ Sie verfügt über die deutlich vereinfachte PDF:

\[f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}x^2}\]

Die CDF der Normalverteilung ist analytisch nicht einfach darzustellen, die Werte können in R aber leicht über die Funktion pnorm (s.u.) abgerufen werden.

In Abbildung 7.14 sind die PDF und CDF für exemplarische Parameterkombinationen dargestellt.

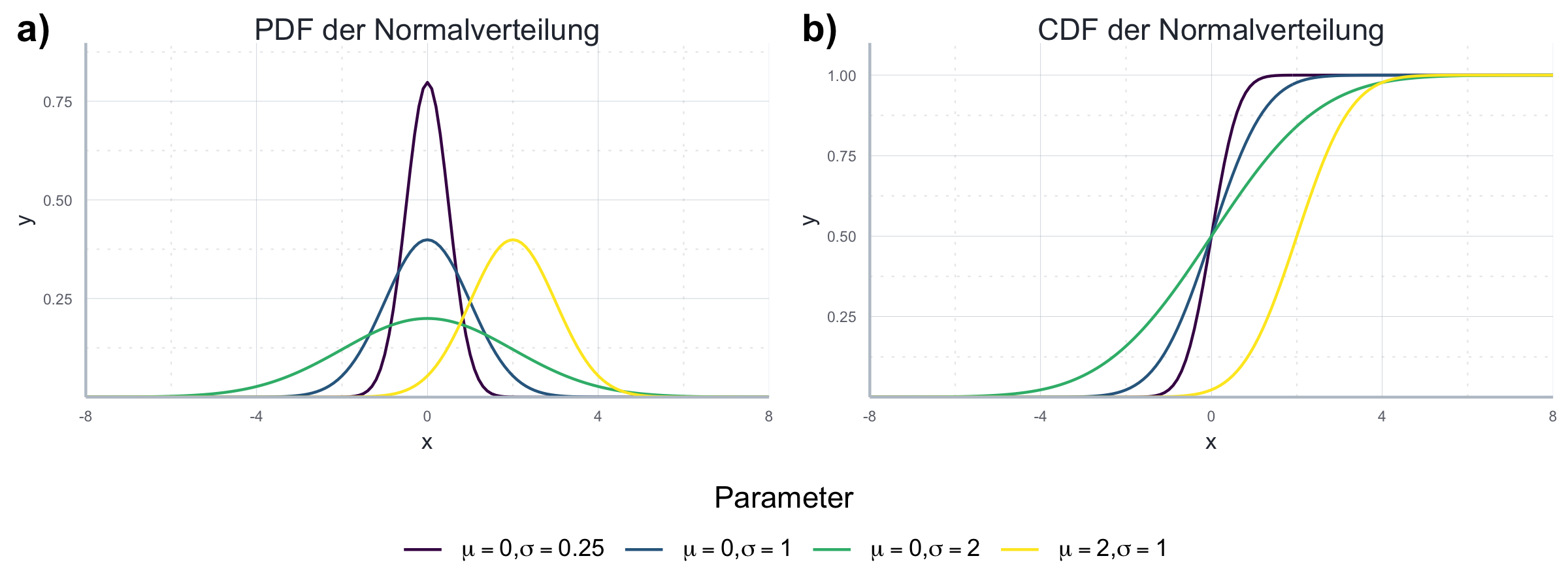
Abbildung 7.14: Vergleich der PDF und CDF der Normalverteilung.

Die Abkürzung in R ist norm. Alle Funktionen nehmen die Paramter \(\mu\) und \(\sigma\) (nicht \(\sigma^2\)) über mean und sd als notwendige Argumente. Ansonsten ist die Verwendung äquivalent zu den vorherigen Beispielen:

dnorm(c(0.5, 0.75), mean = 1, sd = 2) # relative Wahrscheinlichkeiten über PDF

#> [1] 0.1933341 0.1979188

pnorm(c(0.5, 0.75), mean = 1, sd = 2) # Werte der CDF

#> [1] 0.4012937 0.4502618

qnorm(c(0.5, 0.75), mean = 1, sd = 2) # Werte der I-CDF

#> [1] 1.00000 2.34898

norm_sample <- rnorm(5, mean = 1, sd = 2) # 5 Realisierungen der ZV
norm_sample

#> [1]  0.9099446 -0.5698089 -2.3358839  0.2395470  2.8379932

Beispiel zum Zusammenhang dnorm() und qnorm()

7.4.4 Beispiel: die Exponentialverteilung

Sehr häufig wird uns auch die Exponentialverteilung begegnen. Außerhalb der Ökonomik wird sie v.a. zur Modellierung von Zerfallsprozessen oder Wartezeiten verwendet, in der Ökonomik spielt sie in der Wachstumstheorie eine zentrale Rolle. Es handelt sich bei der Exponentialverteilung um eine ein-parametrige Verteilung mit Parameter \(\lambda \in \mathbb{R}^+\) und mit dem Wertebereich \(W_X=[0, \infty ]\).

Die PDF der Exponentialverteilung ist:

\[f(x)=\begin{cases} 0 & x < 0\\ \lambda e^{-\lambda x} & x \geq 0 \end{cases}\]

wobei \(e\) die Eulersche Zahl ist. Die CDF ist entsprechend:

\[F(x)=\begin{cases} 0 & x < 0\\ 1-e^{-\lambda x} & x \geq 0 \end{cases}\]

Beide Verteilungen sind in Abbildung 7.15 dargestellt.

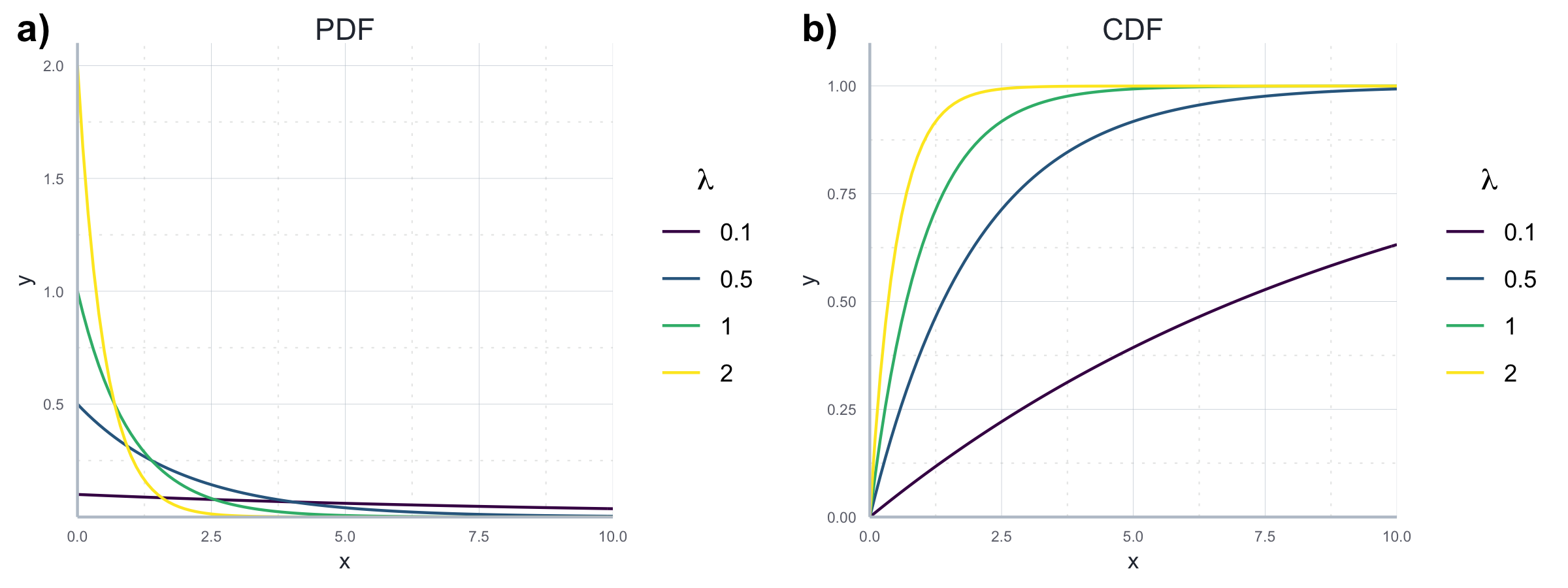
Abbildung 7.15: Beispielhafter Vergleich einer PDF und CDF bei Exponentialverteilung

Der Erwartungswert und die Varianz sind für die Exponentialverteilung äquivalent und hängen ausschließlich von \(\lambda\) ab: \(\mathbb{E}(X)=\sigma_X=\frac{1}{\lambda}\).

Die Abkürzung in R ist exp. Alle Funktionen nehmen den Paramter \(\lambda\) über das Argument rate an:

dexp(c(0.5, 0.75), rate = 1) # relative Wahrscheinlichkeiten über PDF

#> [1] 0.6065307 0.4723666

pexp(c(0.5, 0.75), rate = 1) # Werte der CDF

#> [1] 0.3934693 0.5276334

qexp(c(0.5, 0.75), rate = 1) # Werte der I-CDF

#> [1] 0.6931472 1.3862944

exp_sample <- rexp(5, rate = 1) # 5 Realisierungen der ZV
exp_sample

#> [1] 0.8232605 0.4757590 3.4635949 1.2740277 1.0814852

Es gibt übrigens einen wichtigen Zusammenhang zwischen der stetigen Exponential- und der diskreten Poisson-Verteilung.

7.5 Zusammenfassung Wahrscheinlichkeitsmodelle für einzelne ZV

Tabelle 7.4 fasst noch einmal alle Wahscheinlichkeitsmodelle zusammen, die wir bislang betrachtet haben.

Tabelle 7.4: Überblick der Verteilungen und ihrer Parameter.

Verteilung	Art	Abkürzung	Parameter
Binomialverteilung	Diskret	binom	size, prob
Poisson-Verteilung	Diskret	pois	lambda
Uniform-Verteilung	Kontinuierlich	punif	min, max
Normalverteilung	Kontinuierlich	norm	mean, sd
Exponential-Verteilung	Kontinuierlich	exp	rate

In der statistischen Praxis sind das die Modelle, die wir verwenden, um die DGP (data generating processes) zu beschreiben - also die Prozesse, welche die Daten, die wir in unserer Forschung verwenden, generiert haben.

Deswegen sprechen Statistiker*innen auch häufig von Populationsmodellen. Am besten stellt man es sich mit Hilfe der r*() Funktionen vor: man nimmt an, dass es einen DGP gibt, und dass unsere Daten der Output der r*()-Funktion zum Ziehen von Realisierungen sind. Mit dem Begriff des Populationsmodells macht man dabei deutlich, dass unsere Stichprobe nur eine Stichprobe darstellt - und nicht die gesamte Population aller möglichen Realisierungen des DGP.

Nun wird auch deutlich, warum Kenntnisse in der Wahrscheinlichkeitsrechnung so wichtig sind: wenn wir statistisch mit Daten arbeiten, dann versuchen wir in der Regel über die Daten Rückschlüsse auf den DGP zu schließen. Dafür müssen wir zunächst einmal eine grobe Struktur für den DGP annehmen, und dafür brauchen wir Kenntnisse in der Wahrscheinlichkeitsrechnung und für den entsprechenden Anwendungsfall konkrete Vorannahmen. Dann können wir, gegeben unsere Daten, unsere Beschreibung des DGP verfeinern.

Das bedeutet, dass wir für den DGP ein bestimmtes Wahrscheinlichkeitsmodell annehmen und dann auf Basis unserer Daten die Parameter für dieses Modell schätzen. Dieses Vorgehen nennen wir parametrisch, weil wir hier vor allem Parameter schätzen wollen.⁷¹

7.6 Analyse mehrerer Zufallsvariablen: gemeinsame und marginale Verteilungen

Zum Abschluss dieses Kapitels wollen wir uns noch mit der Analyse von ZV beschäftigen, die ihrerseits aus der Kombination anderer ZV entstehen. Wir wissen ja bereits, dass die Summe oder das Produkt von ZV selbst wieder eine ZV ergibt.⁷² Und diese ‘neuen’ ZV sind genau das, was uns in diesem Abschnitt interessiert. Diese ‘kombinierten’ ZV sind in der Praxis häufig besonders relevant.

Die Verteilungen, die wir bislang kennengelernt haben beschreiben alle die Verteilung einer einzelnen ZV. Anhand der Konzepte der bedingten Wahrscheinlichkeit und der statistischen Unabhängigkeit konnten wir ja schon erahnen, dass es häufig von besonderem Interesse ist, wie mehrere ZV miteinander interagieren. Häufig sind wir daran interessiert, die Verteilung dieser neuen ZV zu charakterisieren. Wir nennen die Verteilung einer ZV, die sich aus mehreren ZV ergibt eine gemeinsame Verteilung. Eine gemeinsame Verteilung gibt uns Informationen über die Wahrscheinlichkeit von Ereignissen, die von allen beteiligten ZV abhängen.

Beispiel: Ein Beispiel für eine praktisch sehr relevante ‘kombinierte’ ZV wäre die gemeinsame Verteilung von Luftverschmutzung und Atemwegserkrankungen. Sowohl der Grad an Luftverschmutzung als auch das Auftreten einer Atemwegserkrankung kann jeweils als isolierte ZV modelliert werden, aber von besonderem Interesse ist natürlich deren gemeinsame Verteilung, bzw. die bedingten Wahrscheinlichkeiten (also für einen bestimmten Grad an Luftverschmutung eine Atemwegserkrankung zu bekommen).

7.6.1 Gemeinsame Verteilungen für diskrete ZV

Nehmen wir einmal an wir haben es mit zwei diskreten ZV Variablen, \(X\) und \(Y\), zu tun. \(X\) kann dabei die Werte \(\{x_1, x_2,...,x_n\}\) und \(Y\) die Werte \(\{y_1, y_2,...,y_n\}\) annehmen. Die gemeinsame Verteilungsfunktion sollte nun Wahrscheinlichkeiten für alle möglichen Kombinationen \(\{(x_1,y_1), (x_1,y_2),...,(x_n,y_m)\}\) angeben. Wir sprechen hier also von einer gemeinsamen PMF \(p_{XY}(x_i,y_j)\) für die gilt:

\[p_{XY}(x_i,y_j)=\mathbb{P}(X=x_i, Y=y_i) \]

Eine solche gemeinsame PMF hat zwei Eigenschaften, ganz analog zur ‘normalen’ PMF:

1. \(0\leq p_{XY}(x_i,y_i)\leq1\): die Wahrscheinlichkeiten für jede Kombination müssen zwischen 0 und 1 liegen;
2. \(\sum_{i=1}^n\sum_{j=1}^m p_{XY}(x_i,y_i)=1\): die Summe aller Einzelwahrscheinlichkeiten ist 1.

Beispiel: das Werfen zweier Würfel Da wir den Wurf eines einzelnen Würfels als diskrete ZV repräsentieren können, können wir den Wurf zweier Würfel als eine gemeinsame diskrete ZV repräsentieren. Grafisch können wir die Wahrscheinlichkeiten recht anschaulich in einer Tabelle abbilden, wobei die einzelnen Zellen jeweils die Werte der gemeinsamen PMF enthalten (siehe Abbildung ??).

\(X\) und \(Y\) beschreiben dabei jeweils die ZV für den ersten und zweiten Würfel.

7.6.2 Gemeinsame Verteilungen für stetige ZV

Die Darstellung des stetigen Falles ist komplett äquivalent: nehmen wir an, \(X\) sei eine stetige ZV mit Wertebereich \([a,b]\) und \(Y\) eine stetige ZV mit Wertebereich \([c,d]\), dann ist der Wertebereich der gemeinsamen PDF \(f_{XY}(x,y)\) gegeben durch \([a,b]\times [c,d]\). Auch für \(f_{XY}(x,y)\) gilt analog zum einfachen Fall:

1. \(p_{XY}(x_i,y_i)\geq0\): die Wahrscheinlichkeitsdichte für jede Kombination muss größer Null sein;
2. \(\int_{c}^d\int_{a}^b f_{XY}(x,y)=1\): das Integral über den gesamten Wertebereich ist 1.

Grafisch könnten wir die gemeinsame PDF als Quadrat darstellen (siehe Abbildung 7.16).

Abbildung 7.16: Gemeinsame Verteilung zweier stetiger ZV. Die Wahrscheinlichkeit eines Events korrespondiert zur Fläche.

7.6.3 Gemeinsame kumulative Verteilungen

Auch die kumulativen Verteilungen für mehrere ZV sind äquivalent zum einfachen Fall definiert. In der allgemeinen Schreibweise schreiben wir:

\[F_{XY}(x,y)=\mathbb{P}(X\leq x, Y\leq y).\]

Für den diskreten Bereich übersetzt sich das konkret in:

\[F_{XY}(x,y)=\sum_{x_i\leq x} \sum_{y_j\leq y}p(x,y) \].

Im kontiniueirlichen Fall ist diese Funktion wieder für den Wertebereich \([a,b]\times [c,d]\) definiert als:

\[F_{XY}(x,y==\int_{c}^d\int_a^b f(x,y)dxdy\].

Wenn wir aus der CDF die PDF herleiten wollen müssen wir die CDF nach beiden Variablen ableiten:

\[f(x,y)=\frac{\partial^2F}{\partial x \partial y}(x,y) \].

Ansonsten sind die Eigenschaften der gemeinsamen CDF wieder vergleichbar zu denen der einfachen CDF (wachsend und für positive/negative Extremwerte von x und y geht der Wert gegen 0/1).

7.6.4 Marginale Verteilungen

Häufig kennen wir die gemeinsame Verteilung von zwei oder mehr ZV und wollen aus dieser gemeinsamen Verteilung die Verteilungen der einzelnen ZV ableiten. Haben wir es z.B. mit einer gemeinsamen Verteilung \(p_{XY}(x,y)\) zu tun wollen wir häufig die separaten Verteilungen \(p_X(x)\) und \(p_Y(y)\) ableiten. Wir sprechen in diesem Fall von der Herleitung einer marginalen Verteilung von \(X\) bzw. \(Y\). Im Ergebnis ist eine marginale Verteilung eine ‘ganz normale’ Verteilung, so wie wir sie vor diesem Abschnitt besprochen haben - der Zusatz ‘marginal’ ergibt sich nur daraus, dass sie aus einer gemeinsamen Verteilung abgeleitet wurde.

Im diskreten Fall erhalten wir die marginalen Verteilungen durch das Aufsummieren bei Konstanthaltung der anderen Variablen. Im Falle der gemeinsamen Verteilung \(p_{XY}(x,y)\) gilt dabei also:

\[p_X(x_i) = \sum_jp(x_i,y_j)\] und

\[p_Y(y_i) = \sum_ip(x_i,y_j)\] Beispiel: Für das oben beschriebene Beispiel des Werfens zweier Würfel können wir die marginale Verteilung des ersten Würfelwurfes (also von \(X\)) auf die in Abbildung ?? dargestellte Art und Weise erhalten. Hier wird auch deutlich, wo der Name ‘marginal’ herkommt: wir betrachten die aufsummierten Wahrscheinlichkeiten ‘am Rand’. Die marginale Verteilung im stetigen Fall hat genau die gleiche Bedeutung wie im diskreten Fall.

7.6.5 Bedingte Verteilungen und bedinge Momente

Die bedingte Verteilung einer ZV beschreibt die Verteilung einer ZV für den Fall dass eine andere ZV auf einen bestimmten Realisationswert bedingt ist. Die Definition ist analog zur allgemeinen bedingten Wahrscheinlichkeit, die wir schon weiter oben eingeführt haben. Daher betrachten wir hier nur ein Beispiel und zwar den folgenden Zusammenhang zwischen \(X\) und \(Y\), wobei gilt, dass \(X:\) “Es schneit” und \(Y:\) “Es ist kalt”. Dann wäre eine gemeinsame Verteilung wie in Tabelle ?? angegeben plausibel. Um aus dieser gemeinsamen Verteilung die bedingte Verteilung von \(Y\) abzuleiten verwenden wir die bereits oben eingeführte Formel:

\[\begin{align} \mathbb{P}(A|B)=\frac{\mathbb{P}(A\cap B)}{\mathbb{P}(B)} \end{align}\]

und passen sie für unseren Verteilungsfall an:

\[\begin{align} \mathbb{P}(X=x | Y=y)=\frac{\mathbb{P}(X=x, Y=y)}{\mathbb{P}(Y=y)} \end{align}\]

Sind wir z.B. an der Wahrscheinlichkeit für Schnee interessiert, gegeben dass das Wetter kalt ist, dann ergibt sich:

\[\begin{align} \mathbb{P}(Y=1 | X=1)=\frac{\mathbb{P}(X=1, Y=1)}{\mathbb{P}(X=1)}=\frac{0.15}{0.3}=0.5 \end{align}\]

Wir können nun die bereits oben beschriebene Eigenschaft der Unabhängigkeit auch noch einmal im Kontext von gemeinsamen Verteilungen formulieren: zwei ZV \(X\) und \(Y\) gelten als unabhängig, wenn die bedingte Verteilung von \(X\) gegeben \(Y\) nicht von \(Y\) abhängt, also gilt, dass \(\mathbb{P}(X=x | Y=y)=\mathbb{P}(X=x)\).

Ganz analog zur Verteilung können wir bedingte Momente (wie den Erwartungswert oder die Varianz) formulieren. Besonders häufig verwendet wird dabei der bedingte Erwartungswert. Ein in diesem Kontext häufig gebrauchtes Konzept ist das Gesetz der wiederholten Erwartungen (law of iterated expectations), das einen Zusammenhang zwischen dem Erwartungswert und dem bedingten Erwartungswert herstellt:

\[\begin{align} \mathbb{E}(X)=\mathbb{E}\left[\mathbb{E}\left(X | Y\right)\right] \end{align}\]

Im diskreten Fall können wir das Konzept noch leichter verdeutlichen. Hier gilt:

\[\begin{align} \mathbb{E}(X)=\mathbb{E}\left[\mathbb{E}\left(X | Y\right)\right] = \sum_i \mathbb{E}\left(X | Y=y_i\right) \cdot \mathbb{P}\left(Y=y\right) \end{align}\]

Für den Fall zweier Würfe ist das nichts anderes aus das Summieren der Zeile, wobei jedes Event mit der Eintrittswahrscheinlichkeit gewichtet wird.

\[\begin{equation} \begin{aligned} \mathbb{E}(X) ={} & \mathbb{E}\left[\mathbb{E}\left(X | Y\right)\right] = \mathbb{E}\left(X | Y=1\right) \cdot \frac{1}{6} + \mathbb{E}\left(X | Y=2\right) \cdot \frac{1}{6} + \mathbb{E}\left(X | Y=3\right) \cdot \frac{1}{6} + \mathbb{E}\left(X | Y=4\right) \cdot \frac{1}{6} + \\ & \mathbb{E}\left(X | Y=5\right) \cdot \frac{1}{6} + \mathbb{E}\left(X | Y=6\right) \cdot \frac{1}{6} \end{aligned} \end{equation}\]

Für den Fall, dass wir am Erwartungswert für eine 6 beim ersten Würfel interessiert sind wäre das also:

\[\begin{equation} \begin{aligned} \mathbb{E}(X=6) ={} &\mathbb{E}\left[\mathbb{E}\left(X=6 | Y\right)\right] = \mathbb{E}\left(X=6 | Y=1\right) \cdot \frac{1}{6} + \mathbb{E}\left(X=6 | Y=2\right) \cdot \frac{1}{6} + \mathbb{E}\left(X=6 | Y=3\right) \cdot \frac{1}{6}\\ & + \mathbb{E}\left(X=6 | Y=4\right) \cdot \frac{1}{6} + \mathbb{E}\left(X=6 | Y=5\right) \cdot \frac{1}{6} + \mathbb{E}\left(X=6 | Y=6\right) \cdot \frac{1}{6}\\ {}={} & \mathbb{E}\left[\mathbb{E}\left(X=6 | Y\right)\right] = \frac{1}{6} \cdot \frac{1}{6} + \frac{1}{6} \cdot \frac{1}{6} + \frac{1}{6}\cdot \frac{1}{6} + \frac{1}{6} \cdot \frac{1}{6} + \frac{1}{6} \cdot \frac{1}{6} + \frac{1}{6} \cdot \frac{1}{6}= \frac{1}{6} \end{aligned} \end{equation}\]

Im Falle der Würfel liegt übrigens ein Beispiel von mean independence vor, denn in diesem Fall gilt:

\[\mathbb{E}(X|Y) = \mathbb{E}(X)\]

Im Falle des doppelten Wüfelwurfes gilt nämlich, dass \(\mathbb{E}(X=6|Y) = \mathbb{E}(X=6)=\frac{1}{6}\).

Das Gesetz der wiederholten Erwartungen funktioniert auch bei abhängigen ZV. Schauen wir noch einmal auf das Beispiel mit der Kälte und dem Schnee und berechnen wir die Erwartung, dass es schneit:

\[\mathbb{E}(Y=1)=\mathbb{E}\left[\mathbb{E}\left(Y=1 | X\right)\right]=0.15\cdot0.3 + 0.07\cdot0.7=0.094\]

Dabei liegt hier keine mean independence vor, denn: \(\mathbb{E}(Y=1)=\mathbb{E}(X=1, Y=1) + \mathbb{E}(X=0, Y=1)=0.22\), aber \(\mathbb{E}(Y=1|X=0)=0.07\) und \(\mathbb{E}(Y=1|X=1)=0.15\). Sie können sich leicht merken, dass für abhängige ZV nie, und für unabhängige ZV immer mean independence bevorliegt (der umgekehrte Fall gilt jedoch nicht!).

Wir werden später im Kontext der Regressionsanalyse noch sehr häufig auf dieses Gesetz und die Konzepte der marginalen und bedingten Verteilungen zurückkommen.

---

64. Wir nennen eine Menge abzählbar wenn sie mit Hilfe der ganzen Zahlen \(\mathbb{N}\) indiziert werden kann. Das bedeutet, dass auch unendlich große Mengen als abzählbar gelten können.↩︎

65. An der Formel wird noch einmal deutlich, dass wenn \(A\) und \(B\) stochastisch unabhängig sind wir nichts von \(B\) über \(A\) und umgekehrt lernen können, also gilt: \(\mathbb{P}(A|B)=\mathbb{P}(A)\) und \(\mathbb{P}(B|A)=\mathbb{P}(B)\).↩︎

66. Aus den Kolmogorow Axiomen oben ergibt sich, dass die Summe all dieser Wahrscheinlichkeiten 1 ergeben muss: \(\sum_{k\geq 1}\mathbb{P}(X=x_k)=1\).↩︎

67. Zu jeder Wahrscheinlichkeitsverteilung gibt es eine eindeutige Wahrscheinlichkeitsfunktion und jede Wahrscheinlichkeitsfunktion definiert umgekehrt eine eindeutig bestimmte diskrete Wahrscheinlichkeitsverteilung.↩︎

68. Die Herleitung finden Sie im Statistikbuch Ihres Vertrauens oder auf Wikipedia.↩︎

69. Die Intervallschreibweise \([0,1]\) ist potenziell verwirrend. Es gilt: \([a,b]=\{x\in\mathbb{R} | a\leq x \leq b\}\) (geschlossenes Intervall), \((a,b)=\{x\in\mathbb{R} | a < x < b\}\) (offenes Intervall), \((a,b)=\{x\in\mathbb{R} | a < x \leq b\}\)(linksoffenes Intervall) und \((a,b)=\{x\in\mathbb{R} | a \leq x < b\}\)(rechtsoffenes Intervall).↩︎

70. Viele Tabellen mit bestimmten Kennzahlen der Normalverteilung beziehen sich auf die Standard-Normalverteilung. Wenn man diese Werte verwenden will, muss man die tatsächlich verwendete Stichprobe ggf. erst z-transformieren. Unter Letzterem versteht man die Normalisierung einer ZV sodass sie den Erwartungswert 0 und die Varianz 1 besitzt. Dies geht i.d.R. für jede ZV \(X\) recht einfach über die Formel \(Z=\frac{X-\mu}{\sigma}\), wobei \(Z\) die standardisierte ZV, \(\mu\) den Erwartungswert und \(\sigma\) die Standardabweichung von \(X\) bezeichnet↩︎

71. Die Alternative, nicht-parametrische Verfahren, nehmen kein konkretes Wahrscheinlichkeitsmodell an, sondern wählen das Modell auch auf Basis der Daten.↩︎

72. Trivialerweise ist die Summe einer ZV und einer normalen Zahl ebenfalls eine ZV. Diese ZV folgt aber einfach der Verteilung der alten ZV, weil ihr anderer ‘Baustein’ rein deterministisch ist. Dieser Fall ist daher weniger interessant (oder problematisch, je nach Perspektive).↩︎