Chapter 8 Wiederholung: Deskriptive Statistik
Bevor wir uns im folgenden Kapitel 9 mit dem Schluss von den Daten auf die Parameter des zugrundeliegenden Wahrscheinlichkeitsmodells beschäftigen, wollen wir uns im Folgenden noch mit Methoden der deskriptiven Statistik beschäftigen: denn zum einen setzt dieser Rückschluss der Daten auf das Populationsmodell voraus, dass wir uns überhaupt mit den Daten auseinandergesetzt haben, zum anderen sollte die Wahl des zugrundeliegenden Populationsmodell und der Art der Schätzung auf Basis der Daten erfolgen - und auch dafür benötigen wir Methoden der deskriptiven Statistik.
Die Methoden der deskriptiven Statistik helfen uns die Daten, die wir erhoben haben möglichst gut zu beschreiben. Die deskriptive Statistik grenzt sich von der induktiven Statistik davon ab, dass wir keine Aussagen über unseren Datensatz hinaus treffen wollen: wenn unser Datensatz also z.B. aus 1000 Schüler*innen besteht treffen wir mit den Methoden der deskriptiven Statistik nur Aussagen über genau diese 1000 Schüler*innen. Mit Methoden der induktiven Statistik würden wir versuchen Aussagen über Schüler*innen im Allgemeinen, zumindest über mehr als diese 1000 Schüler*innen zu treffen. Das ist genau der im Kapitel 7 angesprochene Schluss von den Daten auf den data generating process (DGP).
In diesem Abschnitt beschäftigen wir uns zunächst nur mit der deskriptiven Statistik. Das ist konsistent mit dem praktischen Vorgehen: bevor wir irgendwelche Methoden der induktiven Statistik anwenden müssen wir immer zunächst unsere Daten mit Hilfe deskriptiver Statistik besser verstehen.
Verwendete Pakete
library(here)
library(tidyverse)
library(data.table)
library(ggpubr)
library(latex2exp)
library(MASS)Für die direkte Anwendung in R verwenden wir einen Datensatz zu ökonomischen Journalen, mit dem wir bereits in Kapitel 6 gearbeitet haben:
journal_daten <- fread(
here::here("data/tidy/journaldaten.csv"))
head(journal_daten)#> Kuerzel Titel
#> 1: APEL Asian-Pacific Economic Literature
#> 2: SAJoEH South African Journal of Economic History
#> 3: CE Computational Economics
#> 4: MEPiTE MOCT-MOST Economic Policy in Transitional Economics
#> 5: JoSE Journal of Socio-Economics
#> 6: LabEc Labour Economics
#> Verlag Society Preis Seitenanzahl Buchstaben_pS Zitationen
#> 1: Blackwell no 123 440 3822 21
#> 2: So Afr ec history assn no 20 309 1782 22
#> 3: Kluwer no 443 567 2924 22
#> 4: Kluwer no 276 520 3234 22
#> 5: Elsevier no 295 791 3024 24
#> 6: Elsevier no 344 609 2967 24
#> Gruendung Abonnenten Bereich
#> 1: 1986 14 General
#> 2: 1986 59 Economic History
#> 3: 1987 17 Specialized
#> 4: 1991 2 Area Studies
#> 5: 1972 96 Interdisciplinary
#> 6: 1994 15 LaborDieser Datensatz enthält Informationen über Preise, Seiten, Zitationen und Abonennten von 180 Journalen aus der Ökonomik im Jahr 2004.73
8.1 Kennzahlen zur Lage und Streuung der Daten
Die am häufigsten verwendeten Kennzahlen der deskriptiven Statistik sind das arithmetische Mittel, die Standardabweichung und die Quantile. Für die folgenden Illustrationen nehmen wir an, dass wir es mit einem Datensatz mit \(N\) kontinuierlichen Beobachtungen \(x_1, x_2, ..., x_n\) zu tun haben.
Das arithmetische Mittel ist ein klassisches Lagemaß und definiert als:
\[\bar{x}=\frac{1}{N}\sum_{i=1}^Nx_i\]
In R wird das arithmetische Mittel mit der Funktion mean() berechnet:
avg_preis <- mean(journal_daten[["Preis"]])
avg_preis#> [1] 417.7222Der durchschnittliche Preis der Journale ist also 417.7222222.
Die Standardabweichung ist dagegen ein Maß für die Streuung der Daten und wird als die Quadratwurzel der Varianz definiert:74
\[s_x=\sqrt{Var(x)}=\sqrt{\frac{1}{N-1}\sum_{i=1}^N\left(x_i-\bar{x}\right)^2}\]
Wir verwenden in R die Funktionen var() und sd() um Varianz und
Standardabweichung zu berechnen:
preis_var <- var(journal_daten[["Preis"]])
preis_sd <- sd(journal_daten[["Preis"]])
cat(paste0(
"Varianz: ", preis_var, "\n",
"Standardabweichung: ", preis_sd
))#> Varianz: 148868.335816263
#> Standardabweichung: 385.834596448094Das \(\alpha\)-Quantil eines Datensatzes ist der Wert, bei dem \(\alpha\cdot 100\%\)
der Datenwerte kleiner und \((1-\alpha)\cdot 100\%\) der Datenwerte größer sind.
In R können wir Quantile einfach mit der Funktion quantile() berechnen.
Diese Funktion akzeptiert als erstes Argument einen Vektor von Daten und als
zweites Argument ein oder mehrere Werte für \(\alpha\):
quantile(journal_daten[["Preis"]], 0.5)#> 50%
#> 282quantile(journal_daten[["Preis"]], c(0.25, 0.5, 0.75))#> 25% 50% 75%
#> 134.50 282.00 540.75Diese Werte können folgendermaßen interpretiert werden: 25% der Journale kosten weniger als 134.5 Dollar, 50% der Journale kosten weniger als 282 Dollar und 75% kosten weniger als 540.75 Dollar.
Dabei wird das \(0.5\)-Quantil auch Median genannt. Wie beim Mittelwert handelt es sich hier um einen Lageparameter, der allerdings robuster gegenüber Extremwerten ist, da es sich nur auf die Reihung der Datenpunkte bezieht, nicht auf ihren numerischen Wert.75
Wie im Kapitel 3 für mean() und sd() erklärt,
akzeptieren auch die Funktionen mean(), var(), sd() und quantile() das
optionale Argument na.rm, mit dem fehlende Werte vor der Berechnung eliminiert
werden können:
test_daten <- c(1:10, NA)
quantile(test_daten, 0.75)#> Error in quantile.default(test_daten, 0.75): missing values and NaN's not allowed if 'na.rm' is FALSEquantile(test_daten, 0.75, na.rm = T)#> 75%
#> 7.75Ein häufig verwendetes Steuungsmaß, das im Gegensatz zu Standardabweichung und Varianz robust gegen Ausreißer ist, ist die Quartilsdifferenz:
quantil_25 <- quantile(journal_daten[["Preis"]], 0.25, names = F)
quantil_75 <- quantile(journal_daten[["Preis"]], 0.75, names = F)
quart_differenz <- quantil_75 - quantil_25
quart_differenz#> [1] 406.25Das optionale Argument names=FALSE unterdrückt die Benennung der Ergebnisse.
Wenn wir das nicht machen würde, würde quart_differenz verwirrenderweise
den Namen 75% tragen.
8.2 Korrelationsmaße
Wie wir am Beispiel der Journale in diesem Kapitel gesehen haben, erheben wir für einzelne Untersuchungsobjekte in der Regel mehr als eine Ausprägung. Im vorliegenden Falle haben wir das einzelne Journal z.B. Informationen unter anderem über Preis, Dicke und Zitationen. Häufig möchten wir wissen wie diese verschiedene Ausprägungen miteinander in Beziehung stehen. Zum Beispiel möchten wir wissen, ob dickere Journale tendenziell teurer sind. Neben der wichtigen grafischen Inspektion der Daten, welche wir in Kapitel 5 kennengelernt haben, gibt es dafür wichtige quantitative Maße, die häufig in den Bereich der Korrelationsmaße fallen.
Das einfachste Korrelationsmaß ist die empirische Kovarianz, die für zwei stetige Ausprägungen \(x\) und \(y\) folgendermaßen definiert ist:
\[s_{xy}=\frac{1}{N-1}\sum_{n=1}^N\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right) \]
Wenn wir die empirische Kovarianz für den Bereich \([-1, 1]\) normieren erhalten wir die empirische Korrelation dieser Ausprägungen Handelt es sich bei den beiden Ausprägung um stetige Ausprägungen nennen wir das resultierende Maß den Pearson-Korrelationskoeffizienten:
\[\rho_{x,y}=\frac{s_{xy}}{s_xs_y}, \quad \rho\in[-1,1]\]
wobei \(s_{xy}\) die Kovarianz der Ausprägungen \(x\) und \(y\) und \(s_x\) und \(s_y\) deren Standardabweichung bezeichnet.
Der so definierte Korrelationskoeffizient informiert uns über die Richtung und die Stärke des linearen Zusammenhangs zwischen \(x\) und \(y\). Wenn \(\rho_{x,y}>0\) liegt ein positiver linearer Zusammenhang vor, d.h. größere Werte von \(x_i\) treten in der Tendenz mit größeren Werten von \(y_i\) auf. Hierbei gilt, dass \(\rho_{x,y}=1 \leftrightarrow y_i = a + b x_i\) für \(a\in \mathbb{R}\) und \(b>0\). Umgekehrt gilt, dass wenn \(\rho_{x,y}<0\) ein negativer linearer Zusammenhang vorliegt und \(\rho_{x,y}=-1 \leftrightarrow y_i = a + b x_i\) für \(a\in \mathbb{R}\) und \(b<0\). Bei \(\rho_{x,y}=0\) liegt kein linearer Zusammenhang zwischen den Ausprägungen vor.
Wie wir unten sehen werden, enthält \(\rho\) keine Informationen über nicht-lineare Zusammenhänge zwischen \(x\) und \(y\). Vorsicht bei der Interpretation ist also angebracht.
In unserem Datensatz haben wir z.B. Informationen über die Seitenzahl
(Spalte Seiten) und den Preis von Journalen (Spalte Preis).
Wir könnten uns nun fragen, ob dickere Journale tendenziell teurer sind.
Dazu können wir, wenn wir uns nur für den linearen Zusammenhang interessieren,
den Pearson-Korrelationskoeffizienten mit der Funktion cor() berechnen:
cor(journal_daten[["Preis"]], journal_daten[["Seitenanzahl"]],
method = "pearson")#> [1] 0.4937243Wir sehen also, dass es tatsächlich einen mittleren positiven linearen Zusammenhang zwischen Preis und Seitenzahl zu geben scheint.
Über das Argument method der Funktion cor() können auch andere
Korrelationsmaße berechnet werden: Der
Spearman-Korrelationskoeffizient (method='spearman')
oder der
Kendall-Korrelationskoeffizient (method='kendall')
sind beides Maße, die nur die Ränge der Ausprägungen und nicht deren
numerische Werte berücksichtigen.
Dies macht sie immun gegen Ausreißer und wir müssen keine Annahme über die
Art der Korrelation machen wie beim Pearson-Korrelationskoeffizient, der nur
lineare Zusammenhänge quantifiziert.
Gleichzeitig gehen uns natürlich auch viele Informationen verloren.
Das richtige Maß ist wie immer kontextabhängig und muss entsprechend theoretisch
begründet werden.
Darüber hinaus erlaubt die Funktion cor() über das Argument use noch den
Umgang mit fehlenden Werten genauer zu spezifizieren.
Wenn Sie an der (nicht-standartisierten) Kovarianz interessiert sind, können
Sie diese über die Funktion cov() berechnen, die analog zu cor() funktioniert.
In jedem Fall ist bei der Interpretation von Korrelationen Vorsicht angebracht: da der Korrelationskoeffizient nur die Stärke des linearen Zusammenhangs misst, können dem gleichen Korrelationskoeffizienten sehr unterschiedliche nicht-lineare Zusammenhänge zugrunde liegen. Figure 8.1 illustriert vier verschiedene nicht-lineare Zusammenhänge, welche allerdings je einen Korrelationskoeffizienten von 0 ergeben würden.
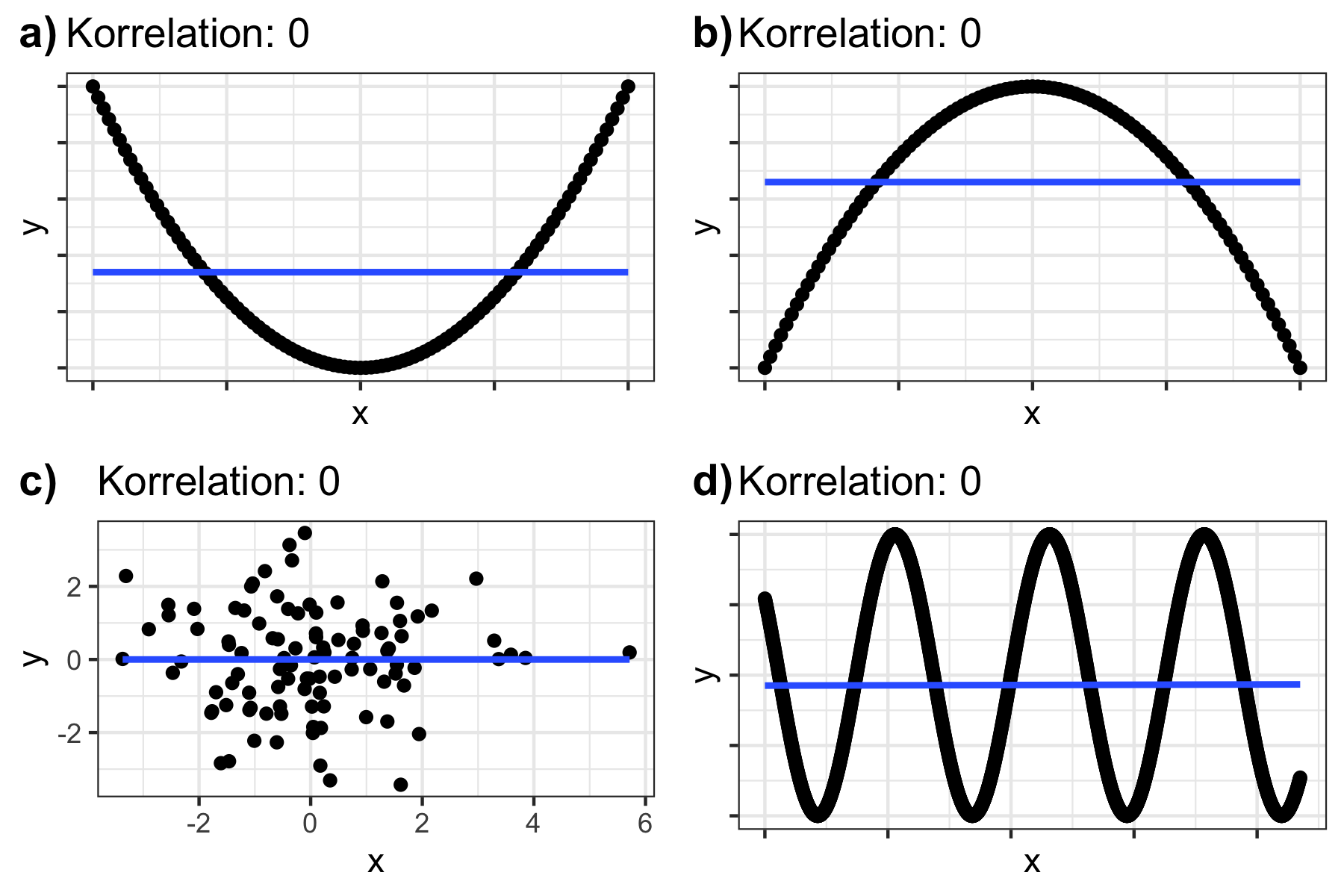
Abbildung 8.1: Unterschiedliche Daten mit gleichen Korrelationswerten.
Daher ist es immer wichtig die Daten auch visuell zu inspizieren, etwa mit den Methoden die wir in Kapitel 5 kennengelernt haben.
8.3 Hinweise zur quantitativen und visuellen Datenbeschreibung
Wie das Beispiel der Korrelationsmaße gerade demonstriert hat, ist bei der Verwendung von quantitativen Maßen zur Beschreibung von Datensätzen immer große Vorsicht geboten. Diese sollten daher immer gemeinsam mit grafischen Darstellungsformen, wie Streudiagrammen oder Histogrammen verwendet werden.
Eine schöne Illustration ist Anscombe’s Quartett (Anscombe 1973).
Dabei handelt es sich um vier Datensätze, die alle (fast exakt) gleiche deskriptive Statistiken aufweisen, jedoch offensichtlich sehr unterschiedlich sind. Diese offensichtlichen Unterschiede werden aber nur durch grafische Inspektion deutlich.
Der Datensatz ist in jeder R Installation vorhanden:
data("anscombe")
head(anscombe)#> x1 x2 x3 x4 y1 y2 y3 y4
#> 1 10 10 10 8 8.04 9.14 7.46 6.58
#> 2 8 8 8 8 6.95 8.14 6.77 5.76
#> 3 13 13 13 8 7.58 8.74 12.74 7.71
#> 4 9 9 9 8 8.81 8.77 7.11 8.84
#> 5 11 11 11 8 8.33 9.26 7.81 8.47
#> 6 14 14 14 8 9.96 8.10 8.84 7.04Tabelle ?? gibt die Werte der quantitativen Kennzahlen an. Die grafische Inspektion in Abbildung 8.2 zeigt, wie unterschiedlich die Datensätze tatsächlich sind.
ans_full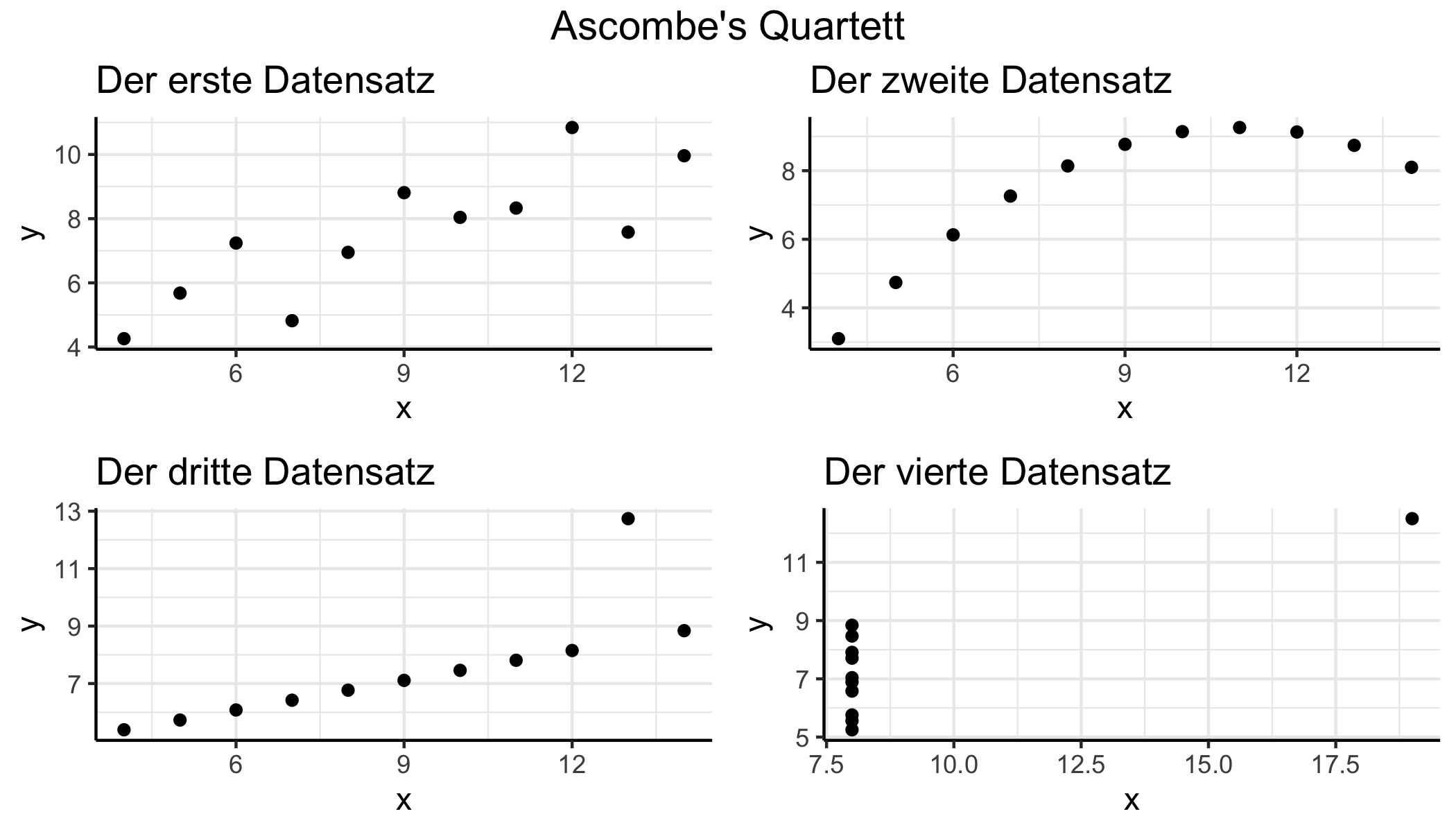
Abbildung 8.2: Unterschiedliche Daten mit gleichen Korrelationswerten.
Interessanterweise ist bis heute nicht bekannt wie Anscombe (1973) seinen Datensatz erstellt hat. Für neuere Sammlungen von Datensätzen, die das gleiche Phänomen illustrieren siehe z.B. Chatterjee und Firat (2007) oder Matejka und Fitzmaurice (2017) . Eine sehr schöne Illustration der Idee findet sich auch auf dieser Homepage, die vom Autor von Matejka und Fitzmaurice (2017) gestaltet wurde.
8.4 Zusamenfassung
In Tabelle 8.1 wollen wir noch einmal die hier besprochenen Funktionen für den Themenbereich ‘Deskriptive Statistik’ zusammenfassen.
| Maßzahl | Funktion | Beschreibung |
|---|---|---|
| Mittelwert | mean() |
Wichtiges Lagemaß; arithmetisches Mittel der Daten |
| Varianz | var() |
Maß für die Streuung; Einheit oft schwer interpretiertbar |
| Standardabweichung | sd() |
Üblichstes Maß für die Streuung |
| \(\alpha\)-Quantil | quantile() |
\(\alpha\cdot 100\%\) der Werte sind kleiner \(\alpha\) |
| Median | quantile(0.5) |
Robustes Lagemaß; die Hälfte der Daten sind größer/kleiner |
| Kovarianz (num. Daten) | cov(method = 'pearson') |
Nicht-normierter linearer Zusammenhang |
| Kovarianz (Ränge) | cov(method = 'kendall') |
Ko-Varianz der Ränge nach der Kendall-Methode |
| Kovarianz (Ränge) | cov(method = 'spearman') |
Ko-Varianz der Ränge nach der Spearman-Methode |
| Pearson Korrelationskoeffizient | cor(method = 'pearson') |
In \([-1, 1]\) normierter linearer Zusammenhang |
| Spearman-Korrelationskoeffizient | cor(method = 'kendall') |
Korrelation der Ränge nach der Kendall-Methode |
| Kendall-Korrelationskoeffizient | cor(method = 'spearman') |
Korrelation der Ränge nach der Spearman-Methode |
Bei den hier verwendeten Daten handelt es sich um eine Übersetzung des Datensatzes
Journalsaus dem PaketAER(Kleiber und Zeileis 2008).↩︎Man beachte den im Vergleich zur Varianzformel für theoretische Modelle modifizierten Nenner \(N-1\)!↩︎
Wenn das teuerste Journal sich im Preis verdoppelt erhöht dies den Mittelwert beträchtlich, ändert den Median aber nicht.↩︎