Chapter 12 Ausgewählte nichtlineare Schätzverfahren
Eine der zentralsten und gleichzeitig restriktivsten Annahmen des OLS Modells ist die Annahme eines linearen Zusammenhangs zwischen der abhängigen und den unabhängigen Variablen. Auch wenn wir im letzten Kapitel gesehen haben wie wir manche nicht-lineare Zusammenhänge durch angemessene Datentransformationen und der Verwendung cleverer funktionaler Formen mit OLS konsistent schätzen können bleiben zahlreiche interessante Zusammenhänge außen vor.
In diesem Kapitel werden wir uns beispielhaft mit dem Fall beschäftigen, in dem unsere abhängige Variable binär ist. Ein typisches Beispiel ist die Analyse von Arbeitslosigkeit. Stellen wir uns vor wir möchten untersuchen unter welchen Umständen Menschen arbeitslos werden. Unsere abhängige Variable \(\boldsymbol{y}\) ist dabei eine binäre Varianble, die entweder den Wert \(0\) annimmt wenn eine Person nicht arbeitslos ist oder den Wert \(1\) annimmt wenn eine Person arbeitslos ist. Unsere Matrix \(\boldsymbol{X}\) enthält dann Informationen über Variablen, die die Arbeitslosigkeit beeinflussen könnten, z.B. Ausbildungsniveau oder Alter. Wir möchten untersuchen wie Variation in den erklärenden Variablen die Wahrscheinlichkeit bestimmt, dass jemand arbeitslos ist, also \(\mathbb{P}(\boldsymbol{y}=\boldsymbol{1} | \boldsymbol{X})\).
Dieser Zusammenhang kann unmöglich als linear aufgefasst werden: es ist unmöglich, dass \(y<0\) oder \(y>1\) und der Zusammenhang im Intervall \([0,1]\) ist quasi nie linear. Daher ist der herkömmliche OLS Schätzer für solche Fälle ungeeignet, denn A1 ist klar verletzt. In diesem Kapitel lernen wir dabei logit- und probit-Modelle als alternative Schätzverfahren kennen.
Verwendete Pakete
library(tidyverse)
library(data.table)
library(here)
library(viridis)12.1 Binäre abhängige Variablen: Logit- und Probit-Modelle
Das folgende Beispiel verwendet angepasste Daten aus Kleiber und Zeileis (2008) zur Beschäftigungssituation von Frauen aus der Schweiz:
schweiz_al <- data.table::fread(
here("data/tidy/nonlinmodels_schweizer-arbeit.csv"),
colClasses = c("double", rep("double", 5), "factor"))
head(schweiz_al)#> Arbeitslos Einkommen_log Alter Ausbildung_Jahre Kinder_jung Kinder_alt
#> 1: 1 10.78750 30 8 1 1
#> 2: 0 10.52425 45 8 0 1
#> 3: 1 10.96858 46 9 0 0
#> 4: 1 11.10500 31 11 2 0
#> 5: 1 11.10847 44 12 0 2
#> 6: 0 11.02825 42 12 0 1
#> Auslaender
#> 1: 0
#> 2: 0
#> 3: 0
#> 4: 0
#> 5: 0
#> 6: 0Wir sind interessiert welchen Einfluss die erklärenden Variablen auf die
Wahrscheinlichkeit haben, dass eine Frau Arbeitslos ist, also die Variable
Arbeitslos den Wert 1 annimmt.
12.1.1 Warum nicht OLS?
Wir könnten natürlich zunächst einmal unser bekanntes und geliebtes OLS Modell
verwenden um den Zusammenhang zu schätzen.
Um die Probleme zu illustrieren schätzen wir in Abbildung 12.1
einmal nur den bivariaten Zusammenhang zwischen Arbeitslos und Einkommen_log.
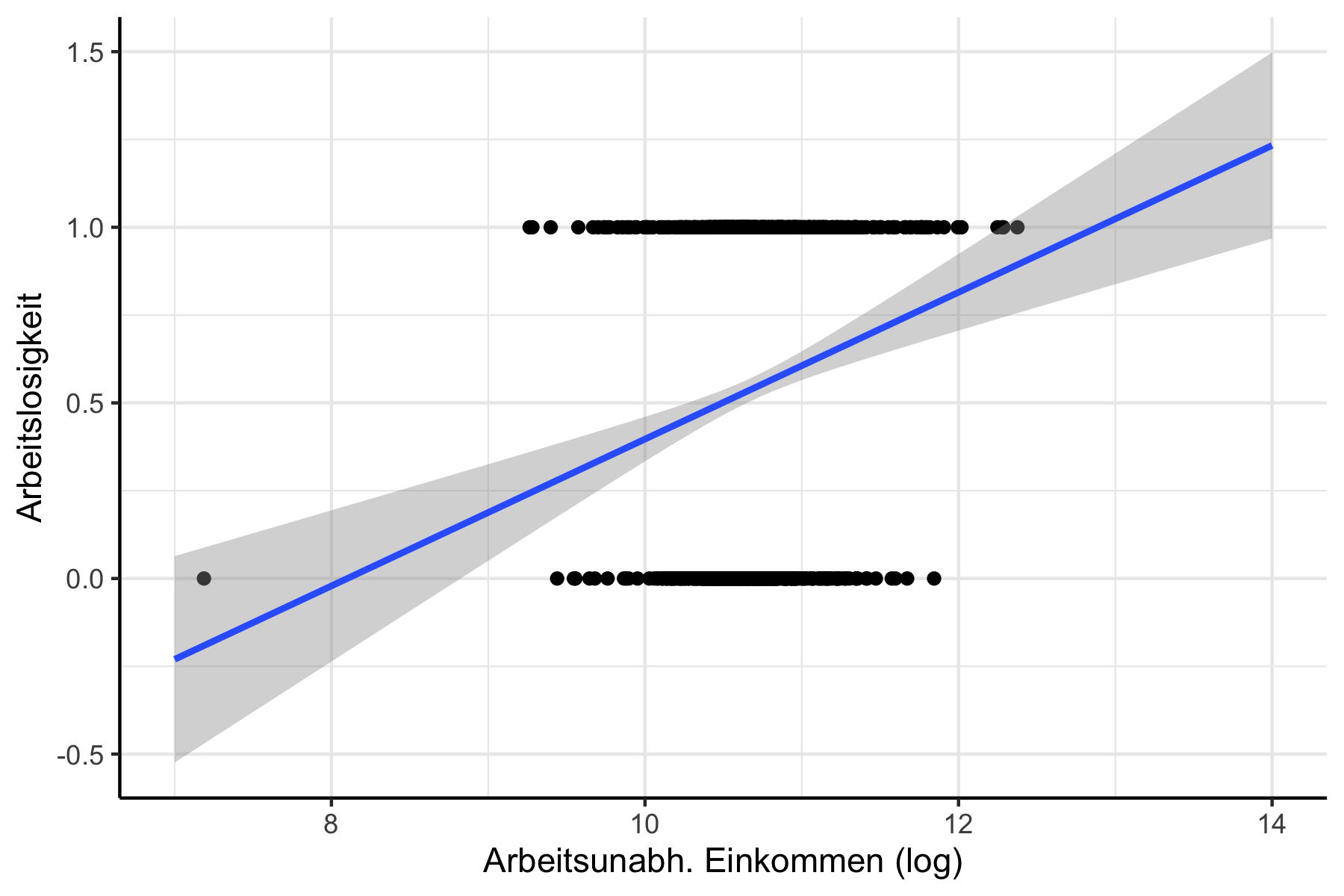
Abbildung 12.1: Schätzung mit OLS Modell.
Unser Modell würde für bestimmte Levels an arbeitsunabhängigem Einkommen Werte außerhalb des Intervalls \(0, 1\) vorhersagen - also Werte, die \(y\) gar nicht annehmen kann und die, da wir die Werte für \(y\) später als Wahrscheinlichkeiten interpretieren wollen, auch gar keinen Sinn ergeben würden.
Unser Ziel ist da eher ein funktionaler Zusammenhang wie in Abbildung 12.2 zu sehen:
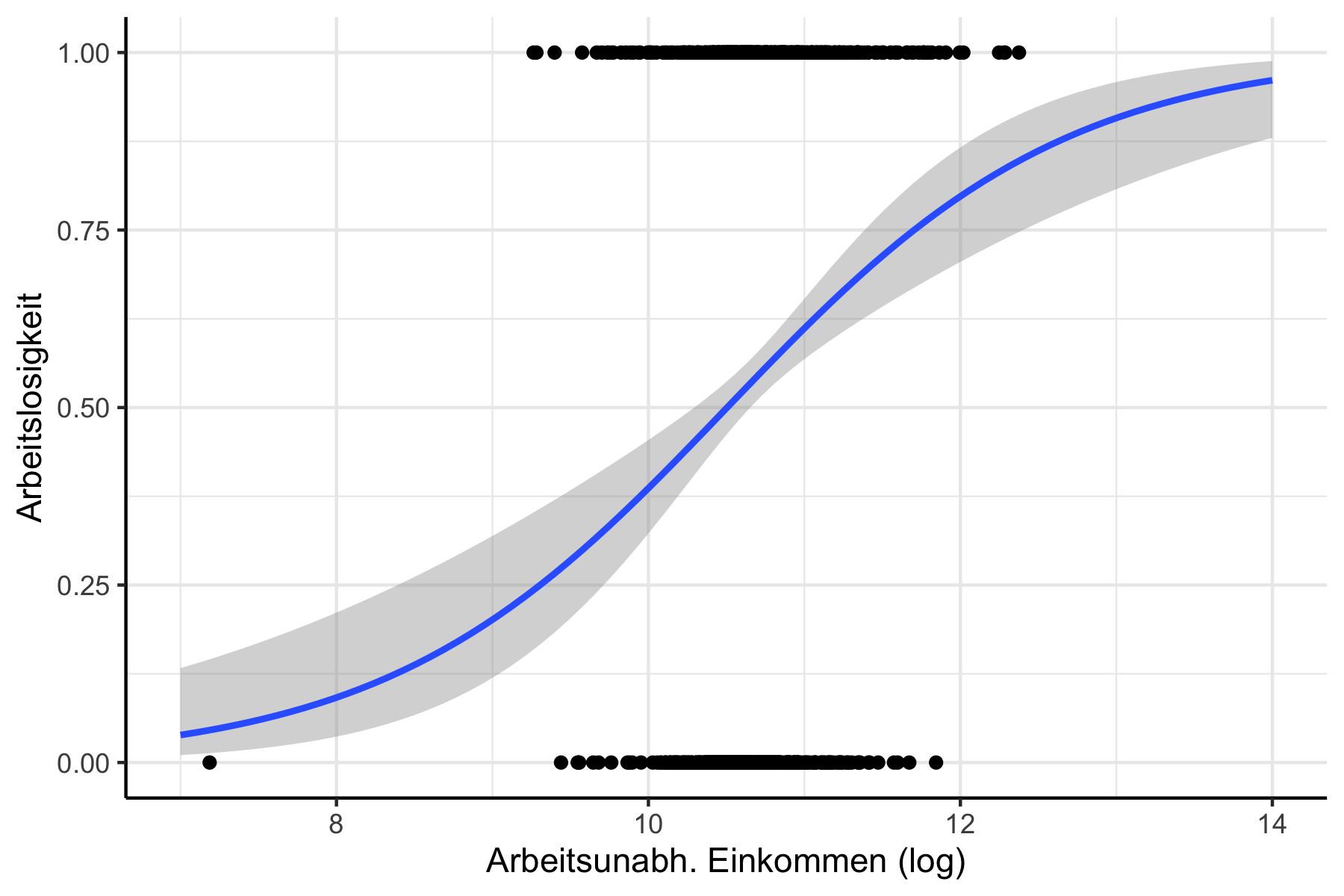
Abbildung 12.2: Funktionaler Zusammenhang, den ein binäres Modell abbilden sollte.
Dieser Zusammenhang ist jedoch nicht linear und damit inkonsistent mit A1 des OLS Modells.
12.1.2 Logit und Probit: theoretische Grundidee
Wir sind interessiert an \(\mathbb{P}(y=1|\boldsymbol{x})\), also der Wahrscheinlichkeit, dass \(y\) den Wert \(1\) annimmt, gegeben die unabhängigen Variablen \(\boldsymbol{x}\).
Eine Möglichkeit \(\mathbb{P}(y=1|\boldsymbol{x})\) auf das Intervall \([0,1]\) zu beschränken ist folgende Transformation:96
\[\begin{align} \mathbb{P}(y=1|\boldsymbol{x})= \frac{\exp(\boldsymbol{X\beta})}{1+\exp(\boldsymbol{X\beta})} \end{align}\]
Diesen Ausdruck können wir dann folgendermaßen umformen:
\[\frac{\mathbb{P}(y=1|\boldsymbol{x})}{1-\mathbb{P}(y=1|\boldsymbol{x})}=\frac{\frac{\exp(\boldsymbol{X\beta})}{1+\exp(\boldsymbol{X\beta})}}{1-\frac{\exp(\boldsymbol{X\beta})}{1+\exp(\boldsymbol{X\beta})}}\] Hier haben wir nun die so genannten odds: das Verhältnist dass \(\mathbb{P}(y=1|\boldsymbol{x})\) und \(\mathbb{P}(y\neq0|\boldsymbol{x})\). Wir multiplizieren nun den linken Teil der Gleichung mit \(1=\frac{\exp(\boldsymbol{X\beta})}{\exp(\boldsymbol{X\beta})}\) um den Zähler durch Kürzen zu vereinfachen:
\[\begin{align} \frac{\mathbb{P}(y=1|\boldsymbol{x})}{1-\mathbb{P}(y=1|\boldsymbol{x})} &= \frac{\exp(\boldsymbol{X\beta})}{\exp(\boldsymbol{X\beta})\cdot \left(\frac{1+\exp(\boldsymbol{X\beta}}{1+\exp(\boldsymbol{X\beta}}- \frac{\exp(\boldsymbol{X\beta})}{1+\exp(\boldsymbol{X\beta})}\right)}\nonumber\\ &= \frac{\exp(\boldsymbol{X\beta})}{\left(1+\exp(\boldsymbol{X\beta})\right)\cdot \frac{1}{1+\exp(\boldsymbol{X\beta})}}\nonumber\\ &=\exp(\boldsymbol{X\beta}) \end{align}\]
Nun können wir durch logarithmieren eine brauchbare Schätzgleichung herleiten:
\[\begin{align} \ln\left(\frac{\mathbb{P}(y=1|\boldsymbol{x})}{1-\mathbb{P}(y=1|\boldsymbol{x})}\right) &= \ln\left(\exp(\boldsymbol{X\beta})\right)\nonumber\\ \ln\left(\frac{\mathbb{P}(y=1|\boldsymbol{x})}{1-\mathbb{P}(y=1|\boldsymbol{x})}\right) &= \boldsymbol{X\beta} \end{align}\]
Wir sprechen hier von dem so genannten logit Modell, da wir hier auf der linken Seite den Logarithmus der Odds haben. Diesen Zusammenhang können wir nun auch ohne Probleme mit unserem OLS-Schätzer schätzen, denn hier haben wir einen klaren linearen Zusammenhang. Nur die abhängige Variable ist auf den ersten Blick ein wenig merkwürdig: der Logarithmus der Odds des interessierenden Events. Aber das ist kein unlösbares Problem wie wir später sehen werden.
probit Modelle funktionieren auf eine sehr ähnliche Art und Weise, verwenden aber eine andere Transformation über die kumulierte Wahrscheinlichkeitsverteilung der Normalverteilung. Hier wird im Endeffekt folgende Regressionsgleichung geschätzt:
\[\begin{align} \mathbb{P}(y=1|\boldsymbol{x})=\phi(\boldsymbol{X\beta}) \end{align}\]
wobei \(\Phi(\cdot)\) die kumulierte Wahrscheinlichkeitsverteilung der Normalverteilung ist.
Logit oder Probit? Wie Sie in Abbildung 12.3 sehen, die sich wieder auf das Einführungsbeispiel bezieht, sind die funktionalen Formen beider Modelle sehr ähnlich. Früher war das Logit-Modell beliebter, weil es etwas technisch etwas leichter zu berechnen war. Mit heutigen Computern ist dieser Vorteil jedoch irrelevant geworden. Es gibt jedoch Fälle in denen Logit-Modelle etwas leichter zu interpretieren sind - für die hier vorgestellte Strategie spielt es jedoch ebenfalls keine Rolle. In einigen Modifikationen binärer Schätzmodelle ist es einfacher, als Ausgangspunkt das Probit-Modell zu nehmen - aber das ist für die meisten Anwendungsfällte ebenfalls egal. Am Ende des Tages gilt: wenn Sie Logit verstanden haben, haben Sie wohl auch Probit verstanden und in der Praxis ist es bis auf wenige Ausnahmen zunächst einmal völlig zweitrangig welches der Modelle Sie verwenden. Eine technisch genauere Diskussion, die Logit und Probit jeweils als Sonderfall der Generalisierten Modelle begreift, siehe z.B. Kapitel 11 in Fitzmaurice, Laird, und Ware (2011).
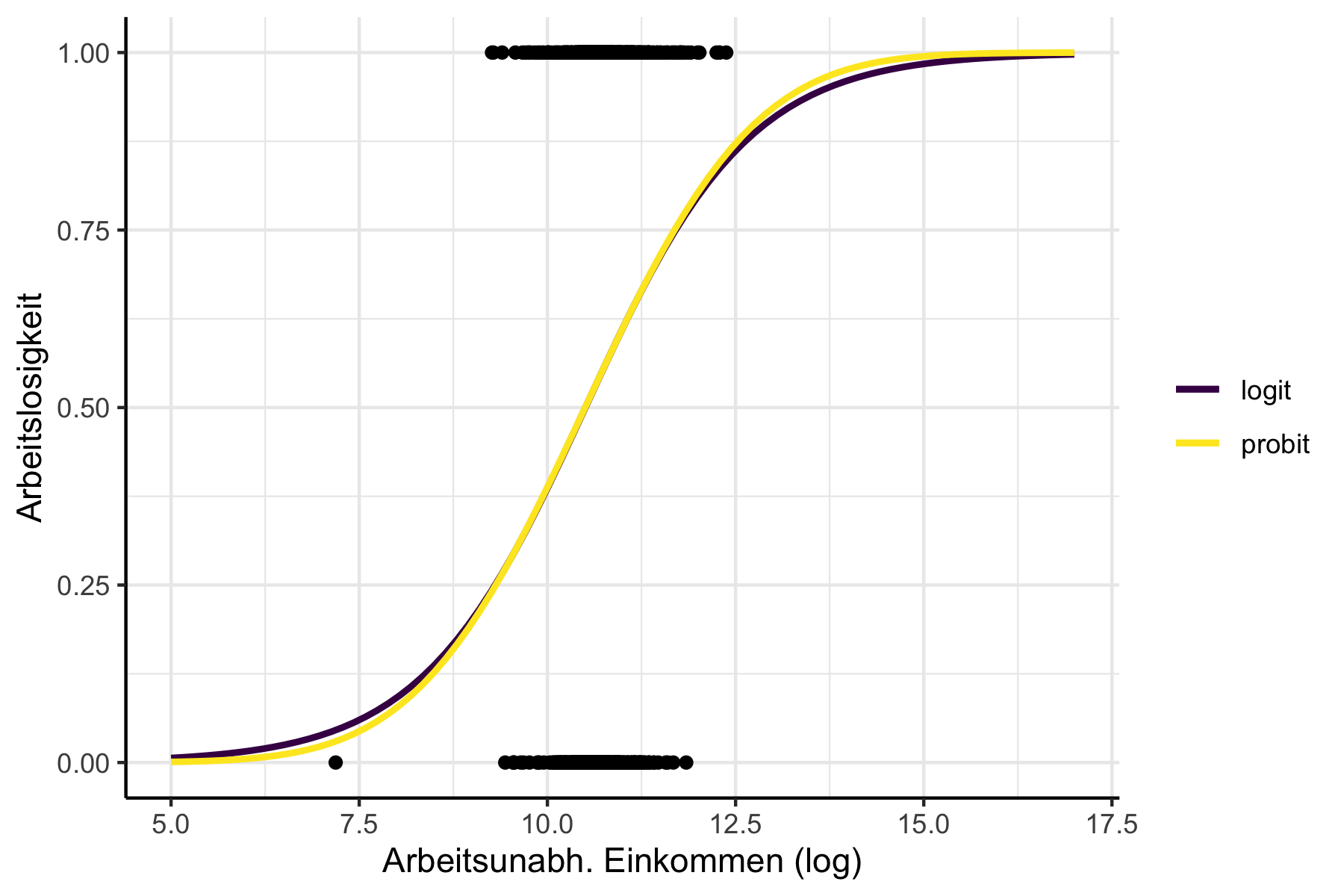
Abbildung 12.3: Vergleich der funktionalen Form bei logit und probit Modellen.
12.1.3 Logit und Probit: Implementierung in R
Da logit und probit Modelle zu den so genannten generalisierten Modellen
gehören verwenden wir die Funktion glm um die Modelle zu schätzen.
Die Spezifikation ist dabei sehr ähnlich zu den linearen Modellen, die wir
mit lm() geschätzt haben.
Nehmen wir einmal an wir wollen mit unserem Datensatz von Schweizerinnen die Effekte von Alter und arbeitsunabhängigem Einkommen auf die Wahrscheinlichkeit der Arbeitslosigkeit schätzen.
Als erstes Argument formula übergeben wir wieder die Schätzgleichung.
In unserem Falle wäre das also Arbeitslos ~ Alter + Einkommen_log.
Als zweites Argument (family) müssen wir die Schätzart spezifizieren.
Für logit Modelle schreiben wir family = binomial(link = "logit"), für
probit Modelle entsprechend family = binomial(link = "probit").
Das letzte Argument ist dann data.
Insgesamt erhalten wir also für das logit-Modell:
arbeitslogit_test <- glm(
Arbeitslos ~ Einkommen_log + Alter,
family = binomial(link = "logit"),
data = schweiz_al)Und das probit-Modell:
arbeitsprobit_test <- glm(
Arbeitslos ~ Einkommen_log + Alter,
family = binomial(link = "probit"),
data = schweiz_al)Für die Schätzergebnisse können wir wie bilang die Funktion summary()
verwenden:
summary(arbeitslogit_test)#>
#> Call:
#> glm(formula = Arbeitslos ~ Einkommen_log + Alter, family = binomial(link = "logit"),
#> data = schweiz_al)
#>
#> Deviance Residuals:
#> Min 1Q Median 3Q Max
#> -1.7448 -1.1855 0.8128 1.1017 1.8279
#>
#> Coefficients:
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) -10.381739 2.003223 -5.183 2.19e-07 ***
#> Einkommen_log 0.920045 0.185414 4.962 6.97e-07 ***
#> Alter 0.018013 0.006612 2.724 0.00645 **
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> (Dispersion parameter for binomial family taken to be 1)
#>
#> Null deviance: 1203.2 on 871 degrees of freedom
#> Residual deviance: 1168.5 on 869 degrees of freedom
#> AIC: 1174.5
#>
#> Number of Fisher Scoring iterations: 4Aber wie sollen wir das interpretieren? Da das ein wenig schwieriger ist beschäftigen wir uns damit im nächsten Abschnitt.
12.1.4 Logit und Probit: Interpretation der Ergebnisse
Wie wir oben gesehen haben ist die abhängige Variable in der Logit-Regression
der Logarithmus der Odds Ratio.
Das ist nicht ganz einfach zu interpretieren.
So bedeutet der Koeffizient für Auslaender1 in folgender Ergebnistabelle,
dass sich die logarithmierte Odds Ratio ceteris paribus um 1.3 Prozent
reduziert, wenn die betroffene Person Ausländerin ist:
arbeitslogit <- glm(
Arbeitslos ~ Einkommen_log + Alter + Ausbildung_Jahre + Kinder_jung +
Kinder_alt + Auslaender,
family = binomial(link = "logit"),
data = schweiz_al)
summary(arbeitslogit)#>
#> Call:
#> glm(formula = Arbeitslos ~ Einkommen_log + Alter + Ausbildung_Jahre +
#> Kinder_jung + Kinder_alt + Auslaender, family = binomial(link = "logit"),
#> data = schweiz_al)
#>
#> Deviance Residuals:
#> Min 1Q Median 3Q Max
#> -2.2681 -1.0675 0.5383 0.9727 1.9384
#>
#> Coefficients:
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) -10.374346 2.166852 -4.788 1.69e-06 ***
#> Einkommen_log 0.815041 0.205501 3.966 7.31e-05 ***
#> Alter 0.051033 0.009052 5.638 1.72e-08 ***
#> Ausbildung_Jahre -0.031728 0.029036 -1.093 0.275
#> Kinder_jung 1.330724 0.180170 7.386 1.51e-13 ***
#> Kinder_alt 0.021986 0.073766 0.298 0.766
#> Auslaender1 -1.310405 0.199758 -6.560 5.38e-11 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> (Dispersion parameter for binomial family taken to be 1)
#>
#> Null deviance: 1203.2 on 871 degrees of freedom
#> Residual deviance: 1052.8 on 865 degrees of freedom
#> AIC: 1066.8
#>
#> Number of Fisher Scoring iterations: 4Im Falle des Probit-Modells ist die Interpretation noch schwieriger, weil der geschätzte Wert \(\hat{\beta}_6\) hier die Änderung im z-Wert der abhängigen Variable angibt – eine Information, die unmittelbar kaum intuitiv zu verarbeiten ist und daher in der Praxis auch nicht groß diskutiert wird.
In jedem Falle wäre es also deutlich schöner wenn wir Änderungen in den
unabhängigen Variablen
als Änderungen in \(\mathbb{P}(y=1|\boldsymbol{x})\) interpretieren könnten.
In unserem Beispiel also: um wie viel Prozent würde die Wahrscheinlichkeit für
Arbeitslosigkeit steigen, wenn es sich bei der betroffenen Person um eine
Ausländerin handelt?
Um dieses Ergebnis zu bekommen bedarf es aber einiger weniger Umformungen, die
in R für Logit und Probit glücklicherweise gleich funktionieren.
Da der Zusammenhang zwischen \(\mathbb{P}(y=1|\boldsymbol{x})\) und den unabhängigen Variablen nicht-linear ist müssen wir für die Vergleiche der Wahrscheinlichkeiten konkrete Werte angeben.
In einem ersten Schritt verwenden wir die Funktion predict, der wir als
erstes Argument object unser geschätztes Modell übergeben.
Als zweites Argument übergeben wir einen data.frame, in dem wir die
relevanten Änderungen und den zu betrachtenden Bereich angeben.
Je nach Anzahl der abhängigen Variablen kann diese Tabelle recht groß werden,
sie ist aber notwendig, da der Zusammenhang zwischen abhängigen und unabhängiger
Variable ja nicht-linear ist.
Als drittes Argument müssen wir noch type = "response" übergeben damit
wir die Vorhersagen auf der Skala der zugrundeliegenden abhänigigen Variable
bekommen, also direkt als Wahrscheinlichkeiten:
predicted_probs <- predict(object = arbeitslogit,
newdata = data.frame(
"Einkommen_log" = c(10, 10),
"Alter"=c(30, 30),
"Ausbildung_Jahre" = c(5, 5),
"Kinder_alt" = c(0, 0),
"Kinder_jung"= c(1, 2),
"Auslaender" = factor(c(0, 0))
),
type = "response")
predicted_probs#> 1 2
#> 0.6175431 0.8593445Das erste Element ist die Wahrscheinlichkeit arbeitslos zu sein für eine
dreißigjährige Frau mit einem
arbeitsunabhänigen Einkommen von \(\exp(10)=22025\), fünfjähiger Ausbildung, keinen
alten Kindern, einem jungen Kind und mit schweizerischer Staatsangehörigkeit.
Die zweite Wahrscheinlichkeit gilt für eine Frau mit den gleichen Eigenschaften
aber zwei jungen Kindern.
Mit diff() bekommen wir gleich den entsprechenden Effekt des zweiten jungen
Kindes auf die Wahrscheinlichkeit arbeitslos zu sein:
diff(predicted_probs)#> 2
#> 0.2418014Die Wahrscheinlichkeit ist also nach dem Modell ca. \(25\%\) größer! Wenn wir wissen wollen ob der Effekt für Ausländerinnen ähnlich ist rechnen wir:
diff(
predict(object = arbeitslogit,
newdata = data.frame(
"Einkommen_log" = c(10, 10),
"Alter"=c(30, 30),
"Ausbildung_Jahre" = c(5, 5),
"Kinder_alt" = c(0, 0),
"Kinder_jung"= c(1, 2),
"Auslaender" = factor(c(1, 1))
),
type = "response")
)#> 2
#> 0.3189543Hier ist der Effekt mit ca. \(32\%\) also noch größer! Zum Vergleich führen wir die gleiche Prozedur auch noch einmal für das Probit-Modell durch:
arbeitsprobit <- glm(
Arbeitslos ~ Einkommen_log + Alter + Ausbildung_Jahre + Kinder_jung +
Kinder_alt + Auslaender,
family = binomial(link = "probit"),
data = schweiz_al)
diff(
predict(
object = arbeitsprobit,
newdata = data.frame(
"Einkommen_log" = c(10, 10),
"Alter"=c(30, 30),
"Ausbildung_Jahre" = c(5, 5),
"Kinder_alt" = c(0, 0),
"Kinder_jung"= c(1, 2),
"Auslaender" = factor(c(1, 1))
),
type = "response")
)#> 2
#> 0.3023284Wie Sie sehen ist der Unterschied marginal. In der Praxis macht es also meist kaum einen Unterschied welches der beiden Modelle Sie verwenden.
12.2 Abschließende Anmerkungen
In diesem Kapitel haben wir uns beispielhaft mit Logit- und Probit-Modellen beschäftigt. ‘Beispielhaft’ weil das Vorgehen bei diesen Modellen repräsentativ für zahlreiche fortgeschrittene Schätzverfahren ist: wir beobachten zuerst, dass die zu analysierenden Daten nicht zu den Standard-Annahmen von OLS passen. Dann überlegen wir uns eine Transformation der Daten, bzw. eine Transformationsstrategie für die Schätzer sodass wir nach einigen Umformungen wieder an einem Punkt ankommen, wo wir das Modell mit OLS schätzen können. Das ist ein weiterer Grund warum ein solides Verständnis der OLS-Methode so wertvoll ist: viele komplexe Schätzer inkludieren diverse Transformationen, können aber an irgendeinem Punkt auf die OLS-Methode (oder, wie sie dann oft bezeichnet wird, die Least Squares-Methode) zurückgeführt werden. Das gilt natürlich nicht für alle, aber für viele in der Anwendung weit verbreiteten ökonometrischen Methoden. Insofern macht das Verständnis von dem hier vorgestellten Vorgehen auch eine Auseinandersetzung mit Schätzmethoden für zensierte Daten (Tobit-Modelle) oder Panel-Daten (z.B. Fixed-Effects-Modelle), sowie fortgeschrittene Techniken wie Instrumentenvariablenschätzung deutlich einfacher. Nichtsdestotrotz warten auch noch viele andere Schätzverfahren, deren Verständnis zwar durch OLS erleichtert wird, die aber nach etwas anderen Prinzipien funktionieren, z.B. die Maximum Likelihood-Methode, der Generalized Methods of Moments-Ansatz oder die zahlreichen nicht-parametrischen Methoden, mit denen wir uns bislang noch gar nicht auseinandergesetzt haben. Es bleibt also spannend!
Falls Sie das \(\exp\left( \cdot\right)\) in der Gleichung verwirrt: das ist nur eine alternative Schreibweise für die Exponentialfunktion um schwer lesbare Exponenten zu vermeiden. Entsprechend wird Ihnen das häufig begegnen. Es gilt aber immer: \(\exp\left(x \right)=e^x\) und damit \(\exp\left(1 \right)=e\approx 2.718\). Probieren Sie es doch mal in
Raus, hier gibt es dafür die Funktion – Achtung!! –exp().↩︎