Chapter 6 Formale Methoden der Sozioökonomie

Refusing to deal with numbers rarely serves the interest of the least well-off.

— Thomas Piketty

In diesem Kapitel werden ausgewählte formale Methoden, die in der sozioökonomischen Forschung besonders häufig verwendet werden, und ihre Implementierung in R eingeführt. Dabei gibt dieses Kapitel selbstverständlich nur einen ersten Einblick und die Auswahl ist notwendigerweise subjektiv.

Allerdings werden die in diesem Kapitel diskutierten Methoden Ihnen einen guten Einblick in die formale Forschung im Bereich der Sozioökonomik geben und Ihnen verdeutlichen wie vielseitig Sie R in Ihrer Forschungstätigkeit - auch abseits klassischer statistischer Anwendungen - verwenden können.

Zunächst werden wir uns mit der Berechnung von Wachstumsraten beschäftigen und dabei besonders die Verwendung von Logarithmen besprechen. Als nächstes werden Grundlagen der Differentialrechnung wiederholt und ihre Implementierung in R eingeführt. Besondere Beachtung findet dabei das Thema der Optimierung, das im Forschungsalltag eine besonders wichtige Rolle spielt.

Als nächstes illustrieren wir die Verwendung von Konzepten aus der linearen Algebra, und werden anhand konkreter Beispiele noch einmal die Allgegenwärtigkeit der linearen Algebra verdeutlichen.

Den Schwerpunkt des Kapitels bildet dann der Abschnitt zu Verteilungen. Die Analyse von Verteilungen spielt eine sehr wichtige Rolle in der Sozioökonomik, da Themen wie Einkommens- und Vermögensverteilung bzw. Ungleichheitsforschung traditionell ein wichtiges Kernthema der Sozioökonomik ausmachen.

Verwendete Pakete

library(here)
library(tidyverse)
library(data.table)
library(ggrepel)
library(ggpubr)
library(latex2exp)
library(matlib)
library(fitdistrplus)
library(moments)
library(ineq)
library(rmutil)
library(viridis)
library(optimx)

Hinweis: Das Paket matlib (Friendly, Fox, und Chalmers 2019) verwenden wir für einige Matrizenoperationen und zum Lösen linearer Gleichungssysteme. Streng genommen ist das Paket nicht dringend nötig, da anstatt der Funktion matlib::Solve() auch die Funktion base::solve() verwendet werden kann. Der Output von matlib::Solve() ist aber schöner und etwas informativer.

6.1 Änderungsraten und die Rolle des Logarithmus

Die sozioökonomische Forschung beschäftigt sich häufig mit Veränderungen über die Zeit. Je nach Fragestellung sind dabei absolute oder relative Änderungen von Interesse.

Um die Änderungsrate einer Variable \(X\) zu berechnen wird folgende Formel verwendet:

\[\frac{X_t-X_{t-1}}{|X_{t-1}|}\cdot100\% = \left(\frac{X_t}{|X_{t-1}|}-1\right)\cdot100\%\]

Selbstverständlich können wir auch die Änderung über mehr als einen Zeitschritt berechnen. Für die durchschnittliche Änderungsrate verwenden wir:

\[\left(\left[ \frac{X_t}{X_{t-s}} \right]^{\frac{1}{s}} -1 \right)\cdot 100\% \]

Umgekehrt können wir den tatsächlichen Wert der Variable \(X\) berechnen wenn wir Informationen über die jährliche Änderungsrate \(x\) haben. Hierbei gilt:

\[X_{t+s}=X_t\left(1+x\right)^s\]

Diese Formel kann auch durch Verwendung der Eulerschen Zahl \(e\) approximiert werden:

\[X_{t+s}=X_t\left(1+x\right)^s \approx X_t\cdot e^{xs} \]

Diese Approximation wird später hilfreich werden, wenn wir Wachstumsraten in logarithmierter Form darstellen wollen.

Wenn \(X_t=4\), \(s=5\) und \(x=0.05\) ergibt sich für den Wert nach \(s\) Zeitschritten also \(X_{t+s}=4\cdot 1.05^5=5.11\). Oder, unter Verwendung der vereinfachten Formel: \(4\cdot e^{0.05\cdot 5}=5.13\).

Natürlich können wir auch Änderungen von prozentualen Größen berechnen. Wenn die Inflation im Jahr 2010 bei 4% und 2011 bei 5% liegt können wir die Änderung folgendermaßen berechnen:

\[\frac{5\%-4\%}{|4\%|}=0.25=25\%\]

Hier von einer 25-prozentigen Änderung zu sprechen ist jedoch nicht eindeutig: damit könnte eine relative Änderung von 25% gemeint sein, oder aber eine absolute Änderung von 25%. Daher sprechen wir bei letzterem von einer Änderung in Prozentpunkten. Im Beispiel haben wir also eine absolute Änderung von einem Prozentpunkt, bzw. eine relative Änderung von 25%.

In R können wir die Funktionen lag() und lead() aus dem Paket dplyr (Wickham u. a. 2019) verwenden um Änderungsraten zu berechnen.⁴⁴ Die Funktion lag() akzeptieren dabei zwei Argumente: den Vektor der Werte und die Anzahl der Schritte, die zurück bzw. vor gesprungen werden sollen.

Entsprechend können wir Änderungsraten folgendermaßen berechnen:

werte <- c(1, 2.2, 3.25, 0.5, 0.1, -0.1, 0.2)
rel_change <- (werte - dplyr::lag(werte)) / abs(dplyr::lag(werte)) * 100
rel_change

#> [1]         NA  120.00000   47.72727  -84.61538  -80.00000 -200.00000  300.00000

Die gleiche Syntax können wir auch für die Arbeit mit einem data.frame verwenden. Hier müssen wir aber darauf achten, die Daten auch tatsächlich nach dem Beobachtungszeitpunkt zu sortieren, damit data.frame::lag(x, 1) auch den vorherigen Wert ausgibt. Dazu verwenden wir die Funktion dplyr::arrange(), welche die Zeilen eines data.frame gemäß einer oder mehrerer Variablen ordnet:

head(beispiel_daten_at, 4)

#>    country      BIP year
#> 1: Austria 37941.04 2018
#> 2: Austria 37140.79 2017
#> 3: Austria 36469.39 2016
#> 4: Austria 36129.03 2015

beispiel_daten_at <- beispiel_daten_at %>%
  dplyr::arrange(year)
head(beispiel_daten_at, 4)

#>    country      BIP year
#> 1: Austria 36123.43 2014
#> 2: Austria 36129.03 2015
#> 3: Austria 36469.39 2016
#> 4: Austria 37140.79 2017

beispiel_daten_at <- beispiel_daten_at %>%
  dplyr::mutate(
    BIP_Wachstum = (BIP-dplyr::lag(BIP))/abs(dplyr::lag(BIP))*100)
beispiel_daten_at

#>    country      BIP year BIP_Wachstum
#> 1: Austria 36123.43 2014           NA
#> 2: Austria 36129.03 2015   0.01550613
#> 3: Austria 36469.39 2016   0.94206769
#> 4: Austria 37140.79 2017   1.84100901
#> 5: Austria 37941.04 2018   2.15464100

Falls wir innerhalb des Datensatzes unterschiedliche Beobachtungsobjekte haben, z.B. verschiedene Länder, müssen wir den Datensatz vor Berechnung der Wachstumsrate gruppieren:

head(beispiel_daten, 4)

#>    country      BIP year
#> 1: Austria 37941.04 2018
#> 2: Germany 35866.00 2018
#> 3: Austria 37140.79 2017
#> 4: Germany 35477.89 2017

beispiel_daten <- beispiel_daten %>%
  dplyr::arrange(country, year) %>%
  dplyr::group_by(country) %>%
  dplyr::mutate(
    BIP_Wachstum = (BIP-dplyr::lag(BIP))/abs(dplyr::lag(BIP))*100
    ) %>%
  dplyr::ungroup()
beispiel_daten

#> # A tibble: 10 x 4
#>    country    BIP  year BIP_Wachstum
#>    <chr>    <dbl> <int>        <dbl>
#>  1 Austria 36123.  2014      NA     
#>  2 Austria 36129.  2015       0.0155
#>  3 Austria 36469.  2016       0.942 
#>  4 Austria 37141.  2017       1.84  
#>  5 Austria 37941.  2018       2.15  
#>  6 Germany 34077.  2014      NA     
#>  7 Germany 34371.  2015       0.862 
#>  8 Germany 34859.  2016       1.42  
#>  9 Germany 35478.  2017       1.78  
#> 10 Germany 35866.  2018       1.09

Häufig werden Wachstumsraten in ihrer lograrithmierten Form präsentiert. Wir können nämlich die Formel zur Berechnung von Änderungsprozessen folgendermaßen approximieren:

\[\left(\left[ \frac{X_t}{X_{t-s}} \right]^{\frac{1}{s}} -1 \right)\approx \ln \left(\frac{X_t}{X_{t-s}}\right)/t=\frac{\ln(X_t)-ln(X_{t-s})}{t}\]

Sie fragen sich vielleicht warum wir uns mit der Verwendung des Logarithmus überhaupt beschäftigen, wo durch die ‘Vereinfachung’ doch eine kleine Ungenauigkeit eingeführt wird? Tatsächlich ist die Verwendung des Logarithmus häufig hilfreich für die grafische Darstellung von Wachstumsraten.⁴⁵

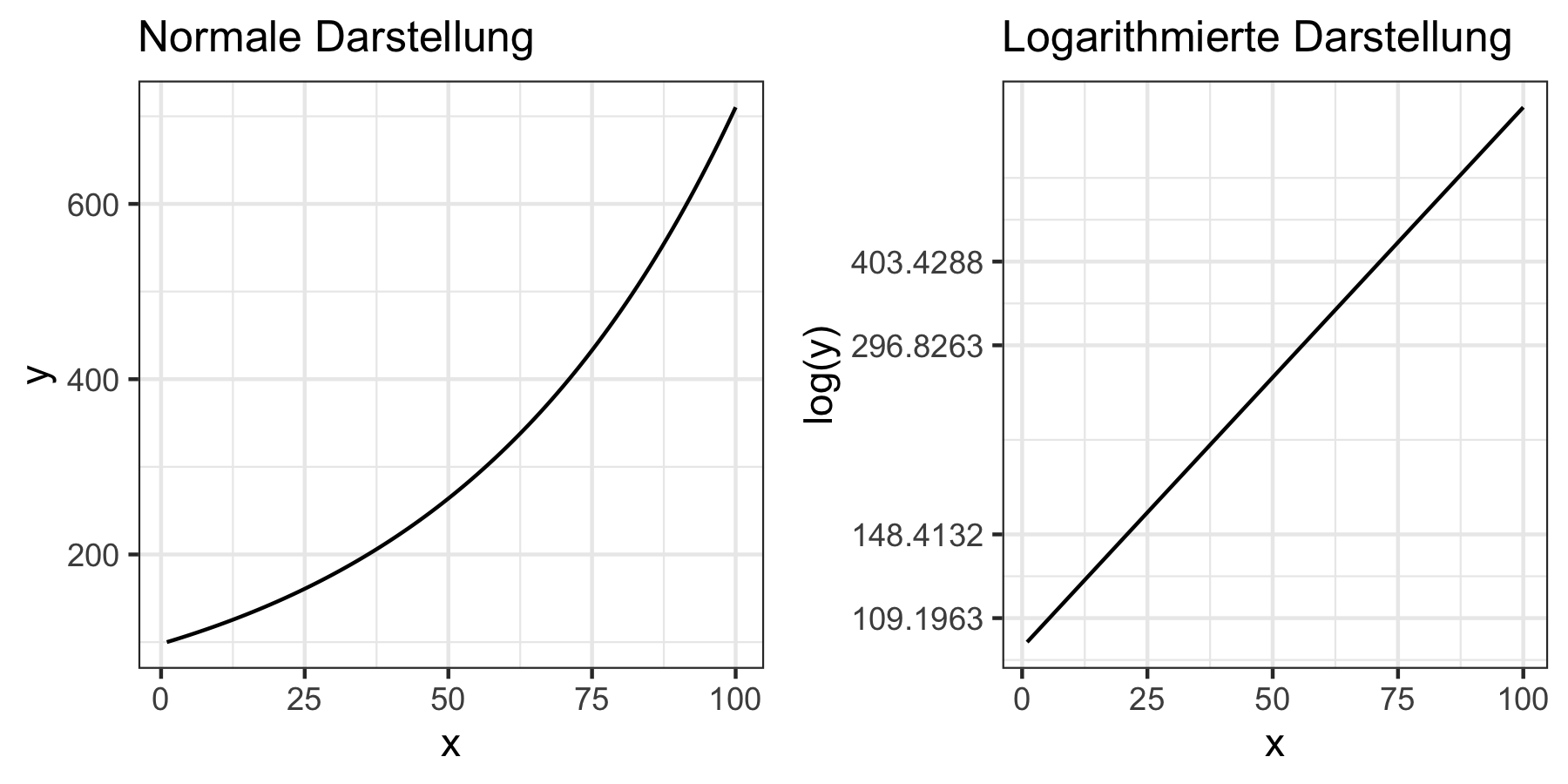
Abbildung 6.1: Vergleich normaler und logarithmierter Darstellung

In Darstellung 6.1 gilt: die Steigung im logarithmierten Plot gibt die relative Änderung der Variable an. Das bedeutet wenn wir im logarithmierten Plot eine lineare Steigung haben wächst die Variable konstant mit der gleichen Wachstumsrate über die Zeit - so wie im obigen Beispiel.

Diese Art der Darstellung ist zum Beispiel bei der langfristigen Betrachtung von Wachstumsraten und dem Vergleich zwischen Ländern sehr hilfreich, da, wie in Abbildung 6.2 Unterschiede in der logarithmierten Darstellung besser erkennbar sind.

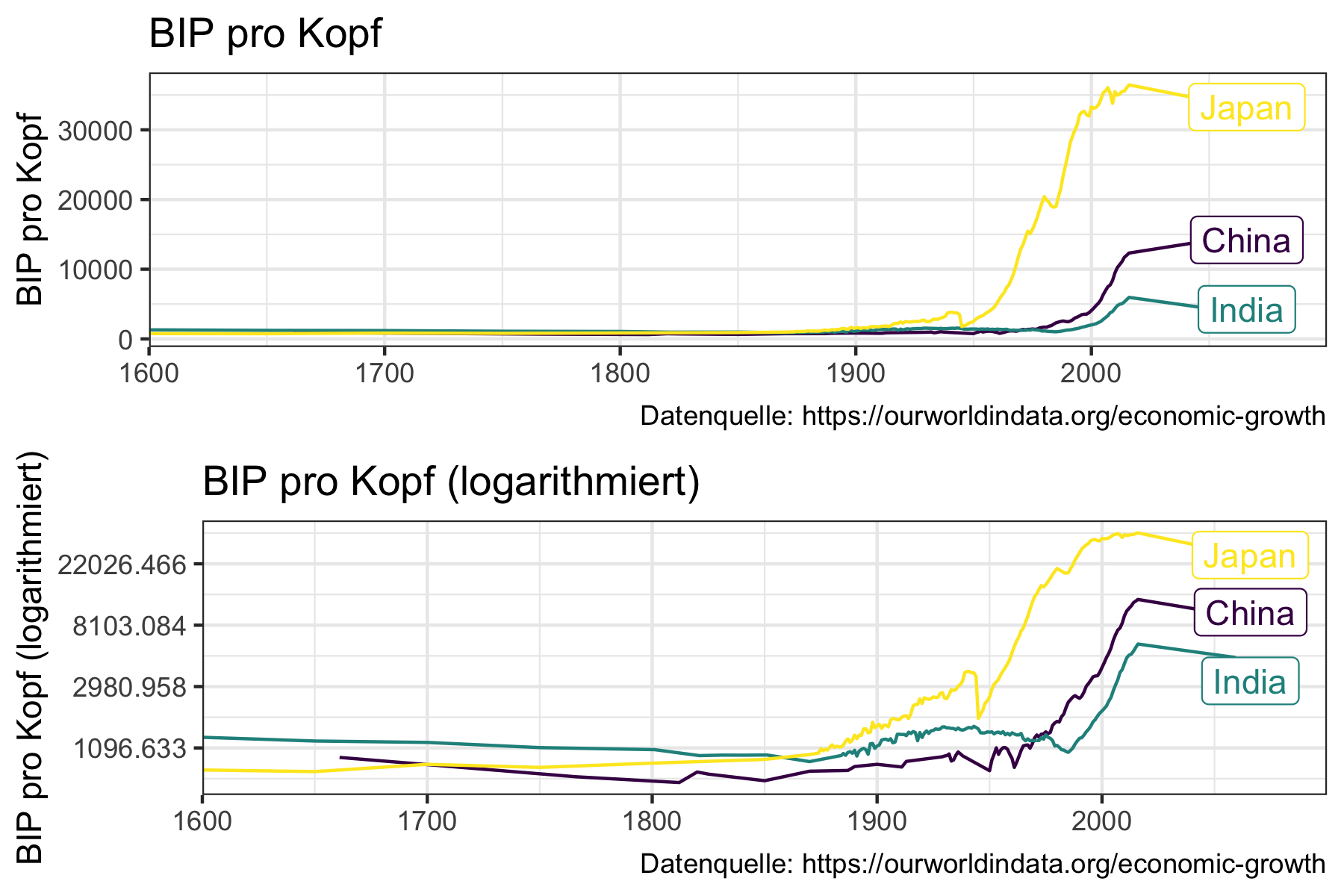
Abbildung 6.2: Vergleich normaler und logarithmierter Darstellung bei langfristiger vergleichender Betrachtung von Wachstumsraten

Abbildung 6.3 zeigt wie wichtig eine solche Darstellung sein kann um Events, die zu sehr unterschiedlichen Zeitpunkten stattgefunden haben, vergleichbar zu machen.

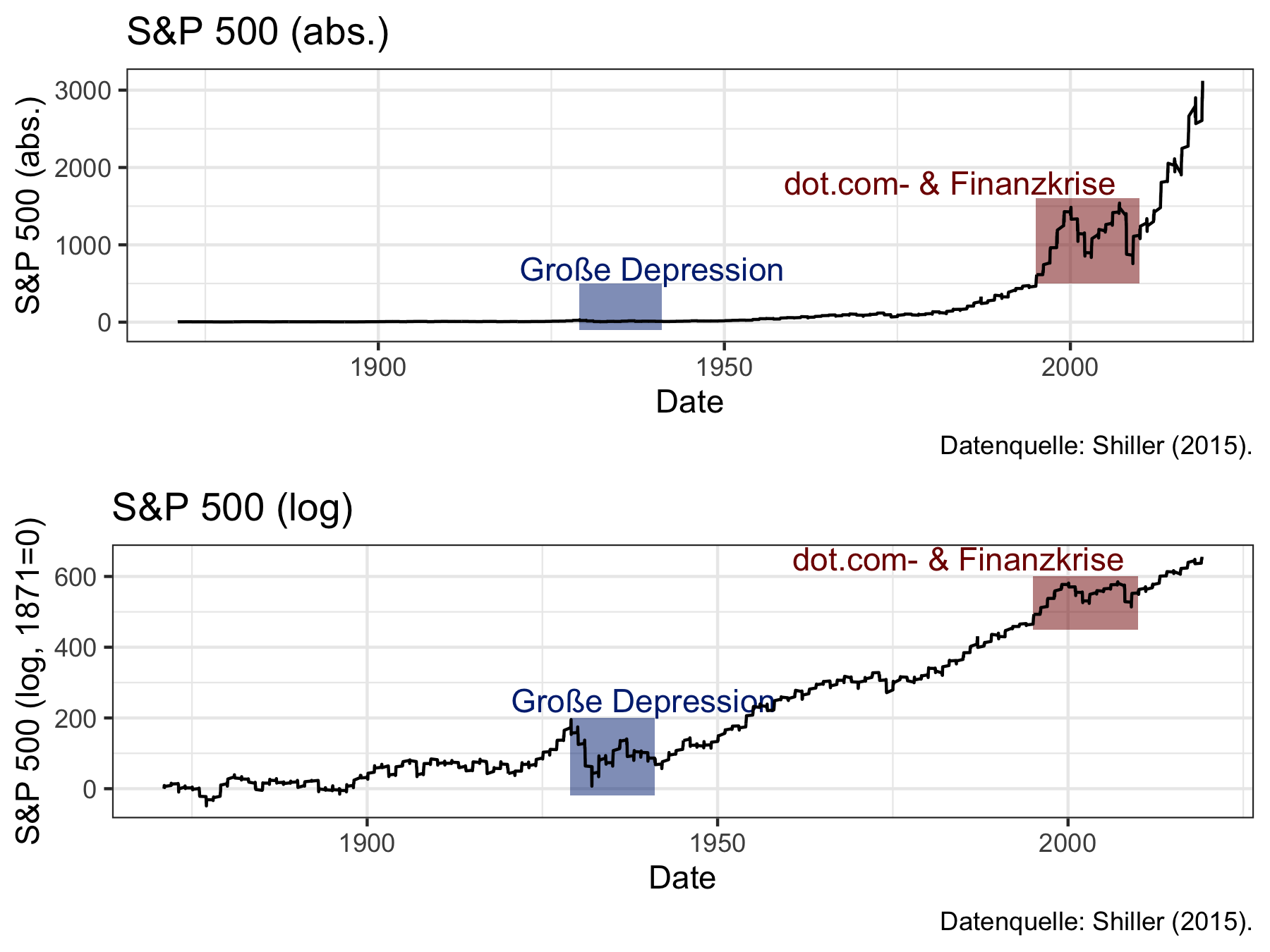
Abbildung 6.3: Vergleich normaler und logarithmierter Darstellung bei Events, die zu sehr unterschiedlichen Zeitpunkten stattgefunden haben

Während die absoluten Zahlen die Volatilität während der Großen Depression verschwindend gering erscheinen lassen wird im unteren Graph von Abbildung 6.3 deutlich, dass die Volatilität damals tatsächlich noch größer war.

Um die Achsen intuitiver verständlich zu machen habe ich von allen Werten den Wert für 1871 (die erste Beobachtung) abgezogen und den Wert für 1871 somit auf Null normiert. Zudem habe ich die Werte mit 100 multipliziert, sodass eine Änderung von 1 auf der y-Ache zu einer einprozentigen Änderung des S&P Kurses korrespondiert.

Im Rahmen der Regressionsanalyse werden wir zudem lernen, dass die logarithmierte Form die Analyse von Wachstumsraten in linearen Regressionsmodellen deutlich vereinfacht (siehe Kapitel 11).

6.2 Grundlagen der Differentialrechnung

6.2.1 Einleitung: Differential- und Integralrechnung

Die Differentialrechnung ist eng verwandt mit der Integralrechnung: in beiden Bereichen studiert man die Veränderungen von Funktionen. Während die Differentialrechnung sich mit der lokalen Änderung einer Funktion beschäftigt, also vor allem versucht die Steigung der durch die Funktion definierten Kurven zu berechnen, studiert die Integralrechnung die Flächen und Volumina, die durch eine Funktion definiert sind. Grafisch bedeutet dies, dass wir bei der Integralrechnung an den Flächen unter einer bzw. zwischen mehrerenKurven interessiert sind

Die beiden Bereiche sind eng miteinander verbunden. Besonders deutlich wird das in dem so genannten Fundamentalsatz der Analysis (auch: Hauptsatz der Differential- und Integralrechnung) deutlich. In der Differentialrechnung leiten wir Funktionen ab und in der Integralrechnung leiten wir Funktionen auf. Der Fundamentalsatz der Analysis zeigt, dass die beiden Vorgehensweise jeweils die Umkehrung des anderen Darstellen: Die Ableitung einer Aufleitung führt zur gleichen Ausgangsfunktion, genauso wie die Aufleitung der Ableitung ebenfalls wieder zur Ausgangsfunktion führt.

In der Ökonomik spielen beide Bereiche eine wichtige Rolle, der Fokus wird in diesem Kapitel jedoch auf der Differentialrechnung liegen, deren Anwendungsgebiet noch einmal breiter ist: wann immer Sie eine Funktion maximieren oder minimieren bedienen Sie sich Methoden der Differentialrechnung. Und Maximierung spielt nicht nur in den herkömmlichen Modellen, die auf dem homo oeconomicus aufbauen, eine wichtige Rolle. Auch in zahlreichen anderen Modellierungsparadigmen und genauso in der Ökonometrie spielt die Maximierung eine wichtige Rolle.

6.2.2 Wiederholung: Ableitungsregeln

Für einfache Funktionen gibt es unmittelbare Ableitungsregeln, die uns für jeden Ausdruck die entsprechende Ableitung geben. Komplexere Ausdrücke versucht man über entsprechende Regeln auf diese einfacheren Ausdrücke zurückzuführen und Ableitungen von komplexeren Funktionen somit ‘Stück für Stück’ durchzuführen. Bei den komplexeren Ableitungsregeln handelt es sich insbesondere um die Summen-, Produkt-, Quotienten- und Kettenregel. Vorher wollen wir uns aber mit den einfachen Grundregeln vertraut machen.

Die Ableitung der Funktion \(f(x)\) wird als \(f'(x)\) oder mit \(\frac{\partial f(x)}{\partial x}\) bezeichnet. Letztere Formulierung ist besonders hilfreich wenn eine Funktion im Bezug auf verschiedene Variablen abgeleitet ist: durch diese Formulierung wird unter dem Bruchstrich noch einmal explizit angegeben nach welcher Variable die Funktion abgeleitet wird.

Grundsätzlich gilt, dass die Ableitung einer Konstanten gleich Null ist:

\[\frac{\partial a}{\partial x} = 0\]

Die Ableitung einer Potenz funktioniert folgendermaßen:

\[\frac{\partial x^n}{\partial x}=nx^{n-1}\]

Besteht unsere komplexere Funktion \(f(x)\) aus der Summe von Teilfunktionen verwenden wir die Summenregel. Diese besagt, dass die Ableitung von \(f(x) = u(x) + v(x)\) einfach die Summe der Ableitungen der Teilfunktionen \(u\) und \(v\) sind:

\[f'(x_0)=u'(x_0) + v'(x_0)\] Wenn wir also die Funktion \(f(x)=3x^2+4x\) ableiten wollen geht dies nach der Summenregel folgendermaßen:

\[\begin{align} f'(x)&=u'(x)+v'(x)\\ u(x)&=3x^2, u'(x)=6x\\ v(x)&=4x, v'(x)=4\\ f'(x)&= 6x + 4 \end{align}\]

Die Summenregel funktioniert natürlich äquivalent auch für den Fall in dem die Teilfunktionen substrahiert werden.

Werden die Teilfunktionen nicht summiert sondern multipliziert verwenden wir die Produktregel. Gehen wir wieder davon aus, dass wir eine komplexe Funktion \(f(x)=u(x)v(x)\) ableiten wollen. Ein Beispiel wäre \(f(x)=(4+x^2)(1-x^3)\), wobei \(u(x)=(4+x^2)\) und \(v(x)=(1-x^3)\).

Insbesondere gilt hier:

\[f'(x)=u'(x)\cdot v(x) + u(x)\cdot v'(x)\]

Wir können die komplexere Gesamtfunktion also ableiten indem wir die einzelnen Teile separat ableiten und jeweils mit den Ausgangsfunktionen multiplizieren. Für unser Beispiel mit \(f(x)=(4+x^2)(1-x^3)\) hätten wir also:

\[\begin{align} f'(x)&=u'(x)\cdot v(x) + u(x)\cdot v'(x)\\ u(x)&=(4+x^2), u'(x)=2x\\ v(x)&=(1-x^3), v'(x)=-3x^2\\ f'(x)&=2x(1-x^3) -3x^2(4+x^2) = -3x^2(4+x^2)+2x(1-3x^3) \\\nonumber \ &= 2x - 12x^2 -5x^4 = x(2-12x-5x^3) \end{align}\]

Wenn die beiden Teilfunktionen dagegen dividiert werden müssen wir die Quotientenregel anwenden. Hier gehen wir also von dem Fall \(f(x)=\frac{u(x)}{v(x)}\) aus, z.B. von \(f(x)=\frac{x^3}{3x}\).

In diesem Fall gilt:

\[ f'(x) = \frac{u'(x)\cdot v(x) - u(x)\cdot v'(x)}{\left(v(x)\right)^2}\]

Für unser Beispiel hätten wir dann:

\[\begin{align} f'(x)&=\frac{u'(x)\cdot v(x) - u(x)\cdot v'(x)}{\left(v(x)\right)^2}\\ u(x)&=x^3, u'(x)=3x^2\\ v(x)&=3x, v'(x)=3\\ f'(x)&=\frac{3x^2\cdot 3x - x^3\cdot3}{(3x)^2}\\\nonumber \ & = \frac{6x^3}{9x^2} = \frac{2}{3}x \end{align}\]

Zuletzt betrachten wir noch die Kettenregel, die es uns erlaubt geschachtelte Funktionen abzuleiten. Darunter verstehen wir Funktionen wie \(f(x)=u(x) \circ v(x)=u(v(x))\).

Hier gilt:

\[(u\circ v)'(x_0) = u'\left(v(x_0)\right) \cdot v'(x_0)\] Man leitet also die ‘innere’ Funktion \(v(x)\) normal ab und multipliziert diese Ableitung mit der Ableitung der ‘äußeren’ Funktion \(u(v)\) an der Stelle \(v(x_0)\). Am einfachsten ist das mit einem Beispiel nachzuvollziehen in dem \(f(x)=\left( x^2+4\right)^2\), also \(u(v)=v^2\) und \(v(x)= x^2+4\).

Insgesamt bekommen wir also:

\[\begin{align} f'(x)&=u'\left(v(x_0)\right) \cdot v'(x_0)\\ u(v)&=v^2, u'(v)=2v\\ v(x)&=x^2+4, v'(x)=2x\\ f'(x)&=2(x^2+4)\cdot 2x \end{align}\]

6.2.3 Ableitungen in R

Sie müssen Ableitungen nicht händisch ausrechnen, sondern können die Funktionen auch in R direkt ableiten lassen. Dazu verwenden wir die Funktion expression() um unsere abzuleitende Funktion zu definieren und dann die Funktion D() um die Ableitung zu bilden.

Betrachten wir folgendes Beispiel:

\[f(x) = x^2 + 3x\]

Zunächst wird die Funktion in eine expression übersetzt:

f <- expression(x^2+3*x)
f

#> expression(x^2 + 3 * x)

Eine solche expression können Sie über die Funktion eval() für konkrete Werte ausrechnen lassen:

x <- 1:5
eval(f)

#> [1]  4 10 18 28 40

Zudem können wir mit der Funktion D() direkt die Ableitung einer expression berechnen:

D(f, "x")

#> 2 * x + 3

Wir haben also:

\[\frac{\partial f(x) }{\partial x}=2x+3\]

Wir können Aufrufe von D() auch verschachteln um höhere Ableitungen zu berechnen:

D(D(f, "x"), "x")

#> [1] 2

Für die zweite Ableitung erhalten wir also dementsprechend:

\[\frac{\partial f(x) }{\partial x^2}=2\]

6.2.4 Maximierung: die analytische Perspektive

Eine der wichtigsten Anwendungen der Differentialrechnung ist die Berechnung von Minima und Maxima, so genannten Extrema, einer Funktion. Die interessierende Funktion wird in diesem Kontext in der Regel Zielfunktion genannt.

Die Differentialrechnung spielt hier eine wichtige Rolle, denn Extrema sind dadurch gekennzeichnet, dass die Ableitung einer Funktion an ihren Extrempunkten gleich Null ist. Weil die Nullstellen einer Funktion wiederum recht leicht zu finden sind, bietet es sich an, Extrema über die Ableitung einer Funktion zu suchen.

Die genauen Details des Verfahrens werden hier nicht besprochen, es gibt jedoch zahlreiche gute Lehrbücher. Hier soll es eher um die grundsätzliche Intuition gehen.

Wichtig ist die Unterscheidung zwischen lokalen und globalen Extremwerten. Das globale Maximum (Minimum) liegt an dem Punkt im Definitionsbereich einer Funktion, der zu dem größten (kleinsten) Wert im Wertebereich der Funktion führt. Das lokale Maximum (Minimum) ist für eine bestimmte Teilmenge des Definitionsbereichs der Funktion definiert und bezeichnet den Punkt mit dem größten (kleinsten) Wert innerhalb dieser Teilmenge.

Formal exakt können wir die Punkte folgendermaßen definieren, wenn wir von einer Funktion \(f\) mit Definitionsbereich \(D\subseteq\mathbb{R}\) und Wertebereich \(\mathbb{R}\), also \(f: D\rightarrow \mathbb{R}\) ausgehen.

Dann hat \(f\) ein lokales Minimum im Intervall \(I=(a,b)\) am Punkt \((x^*, f(x^*))\) wenn \(f(x^*)\leq f(x) \forall x \in I \cap D\). Analog sprechen wir bei dem Punk \((x^*, f(x^*))\) von einem lokalen Maximum im Intervall \(I=(a,b)\) wenn \(f(x^*)\geq f(x) \forall x \in I \cap D\).

Wir sprechen beim Punkt \((x^*, f(x^*))\) von einem globalen Minimum wenn \(f(x^*)\leq f(x) \forall x \in x \in D\) und von einem globalen Maximum wenn \(f(x^*)\geq f(x) \forall x \in x \in D\).

In Abbildung 6.4 sehen wir beispielhaft die Extremwerte der Funktion \(f(x)=8x^2 + 2.5x^3 - 4.25x^4 + 2\).

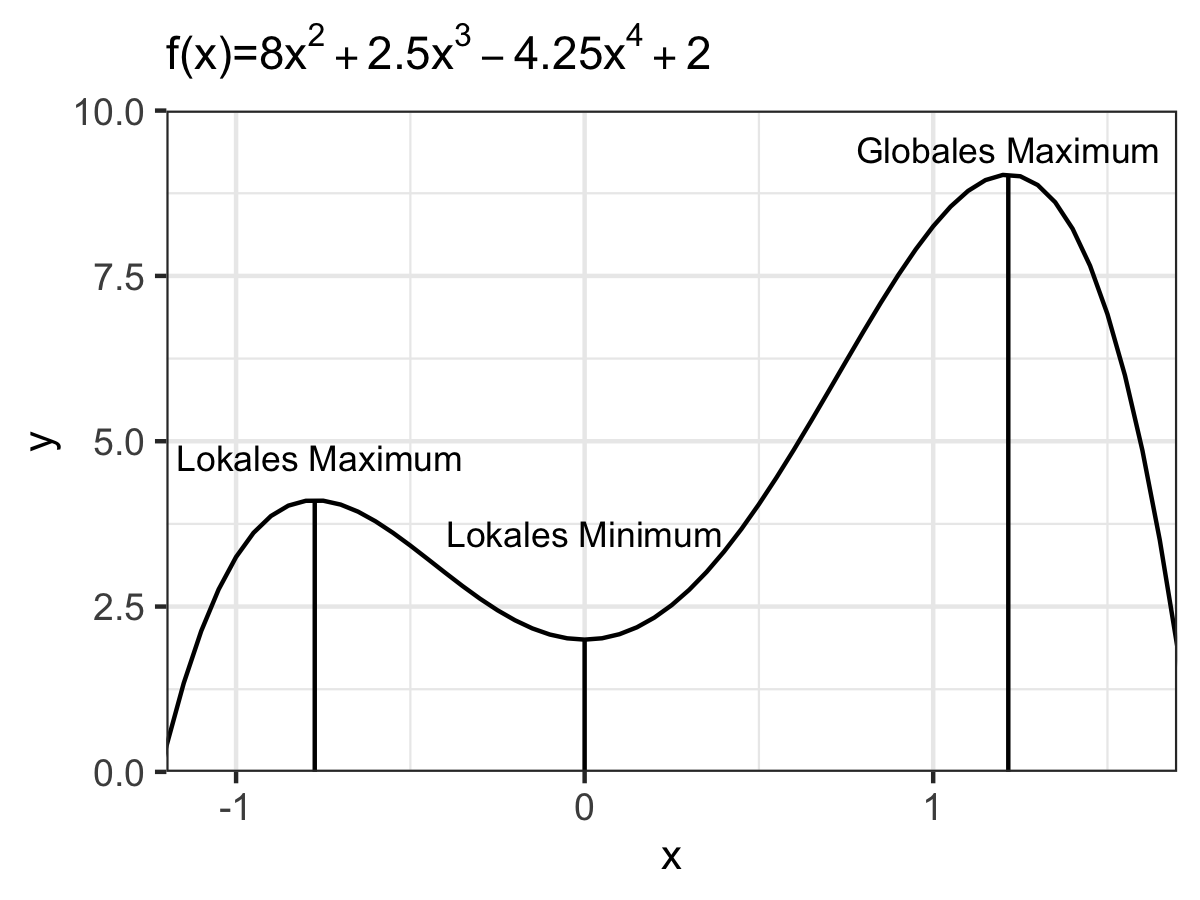
Abbildung 6.4: Beispiel für Extremwerte

Es kann gezeigt werden, dass eine notwendige Bedingung für die Existenz eines Extremwertes am Punkt \(x^*\) ist, dass \(f'(x^*)=0\). Daher ist der erste Schritt bei der analytischen Suche nach Extremwerten immer die Ableitung der Funktion und die Identifikation der Nullstellen. Als nächstes untersucht man die hinreichenden Bedingungen, die einem genauere Informationen über den Punkt geben.

Hierbei hat sich die in Tabelle 6.1 zusammengefasste Heuristik in der Praxis bewährt:⁴⁶

Tabelle 6.1: Heuristik zur Untersuchung der hinreichenden Bedingung.

1. Ableitung	2. Ableitung	Ergebnis
\(f'(x)=0\)	\(f''(x)>0\)	Minimum
\(f'(x)=0\)	\(f''(x)<0\)	Maximum
\(f'(x)=0\)	\(f''(x)=0\)	Wendepunkt

Das Ganze funktioniert natürlich nur wenn eine Funktion auch tatsächlich eine Ableitung besitzt, es sich also um eine differenzierbare Funktion handelt. Daher wird das auch in vielen ökonomischen Modellen angenommen.

Um herauszufinden ob es sich um ein globales Extremum handelt müssen wir die Werte der Extrema vergleichen. Es gibt auch noch einige Heuristiken für besondere Sub-Klassen von Funktionen, die wir hier aber nicht genauer diskutieren wollen.

Wenn die Funktion unter bestimmten Bedingungen maximiert (minimiert) werden soll, sprechen wir von einer Maximierung unter Nebenbedingung(en). Die Standard-Methode hier ist die sogenannte Lagrange-Optimierung. Details finden sich in zahlreichen Lehrbüchern, z.B. in Wainwright und Chiang (2005).

6.2.5 Maximierung: die algorithmische Perspektive

Bei vielen Funktionen wäre die analytische Berechnung von Extrema zu aufwendig oder gar nicht möglich. Daher verwendet man den Computer um die Extrema zu finden. Ironischerweise ist das gerade bei einfachen Funktionen kein großes Problem. Für die im linken Teil der Abbildung XX dargestellte Funktion kann der Computer einfach mit einem beliebigem Startwert \(x_0\) beginnen und sich auf dem Definitionsbereich in Richtung steigender Funktionswerte fortbewegt bis er den Punkt \(x^*_{globmax}=0\) erreicht. Für Funktionen mit lokalen Extremwerten wie im rechten Teil von Abbildung funktioniert diese Strategie unter Umständen nicht mehr, da der Computer leicht auf lokalen Optima “steckenbleibt”. Im Beispiel in Abbildung 6.5 besteht bei einer unglücklichen Wahl des Startwertes die Gefahr, auf dem lokalen Extremum bei \(x=0.77\) hängen zu bleiben.

Abbildung 6.5: Beispiel für die Gefahr auf einem lokalen Extremum hängen zu bleiben (rechter Graph).

Um das zu vermeiden verwenden die Optimierungsalgorithmen einige Tricks. Für die R-Funktion optim() können Sie z.B. zwischen sieben solcher ausgefeilter Algorithmen wählen. Schauen Sie einmal in die Hilfefunktion wenn Sie mehr Informationen über diese Algorithmen bekommen möchten.⁴⁷

Wichtig zu unterscheiden ist die Art der zu optimierenden Funktion und der Nebenbedingungen. Grob können wir zwischen den folgenden drei Fällen unterscheiden:

1. Lineares Programmieren (LP): Sowohl Zielfunktion als auch Nebenbedingungen sind linear. Beispiel: \(\max s.t. Ax<b, x\geq 0\)
2. Quadratisches Programmieren (QP) Zielfunktion ist quadratisch, Nebenbedingungen sind linear. Beispiel: \(\max s.t. Ax<b, x\geq 0\)
3. Nicht-lineares Programmieren (NLP): Die Zielfunktion oder zumindest eine Nebenbedingung ist nicht-linear.

Die Unterscheidung spielt eine ähnliche Rolle wie die Unterscheidung verschiedener Skalenstufen bei der Datenanalyse: je nach Art des Problems müssen wir andere Methoden anwenden. In diesem Fall bedeutet das, dass wir für unterschiedliche Arten von Funktionen andere Pakete verwenden müssen um Extremwerte zu finden. Zusätzlich gibt es aber auch noch ein paar general-purpose-Funktionen, die wir auf alle Klassen anwenden können - auf Kosten der Performance. Diese sind in Tabelle 6.2 zusammengefasst.⁴⁸

Das Schöne ist, dass trotz der Vielzahl an Paketen alle Optimierungsfunktionen nach einem sehr ähnlichen Schema aufgebaut sind. Die ersten beiden Argumente sind immer die Zielfunktion und die Nebenbedingungen. Danach folgen Argumente mit denen Sie die Suchintervalle, den konkreten Algorithmus oder weitere Spezifika festlegen können. Für eine genauere Einführung bietet sich auch die Lektüre der Vignette für das allgemein gehaltene Paket optimx (Nash und Varadhan 2011) an, die hier abgerufen werden kann.

Tabelle 6.2: Generell anwendbare Optimierungsfunktionen.

Art	Optimierungsfunktion	Paket
Allgemein (eindimensional)	optimize()	stats
Allgemein (mehrdimensional)	optimr()	optimx
LP	lp()	lpSolve
QP	solve.QP()	quadprog
NLP	optimize()	optimize
NLP	optimx()	optimx

Im Folgenden wollen wir anhand einiger einfacher Beispiele sehen wie Sie Optimierungsprobleme in R lösen können. Für eine tiefergehende Auseinandersetzung verweisen wir auf die entsprechenden spezialisierten Einführungen.

Betrachten wir die folgende Zielfunktion:

\[\begin{align} f(x)=8x^2 + 2.5x^3 - 4.25x^4 + 2 \end{align}\]

In R:

f_1 <- function(x) 8*x^2 + 2.5*x**3 - 4.25*x**4 + 2

Die Funktion ist in Abbildung 6.6 dargestellt. Wie man sieht verfügt sie über ein lokales Maximum bei \(x_a=-0.77\), ein lokales Minimum bei \(x_b=0\) und ein globales Maximum bei \(x_c=1.22\).

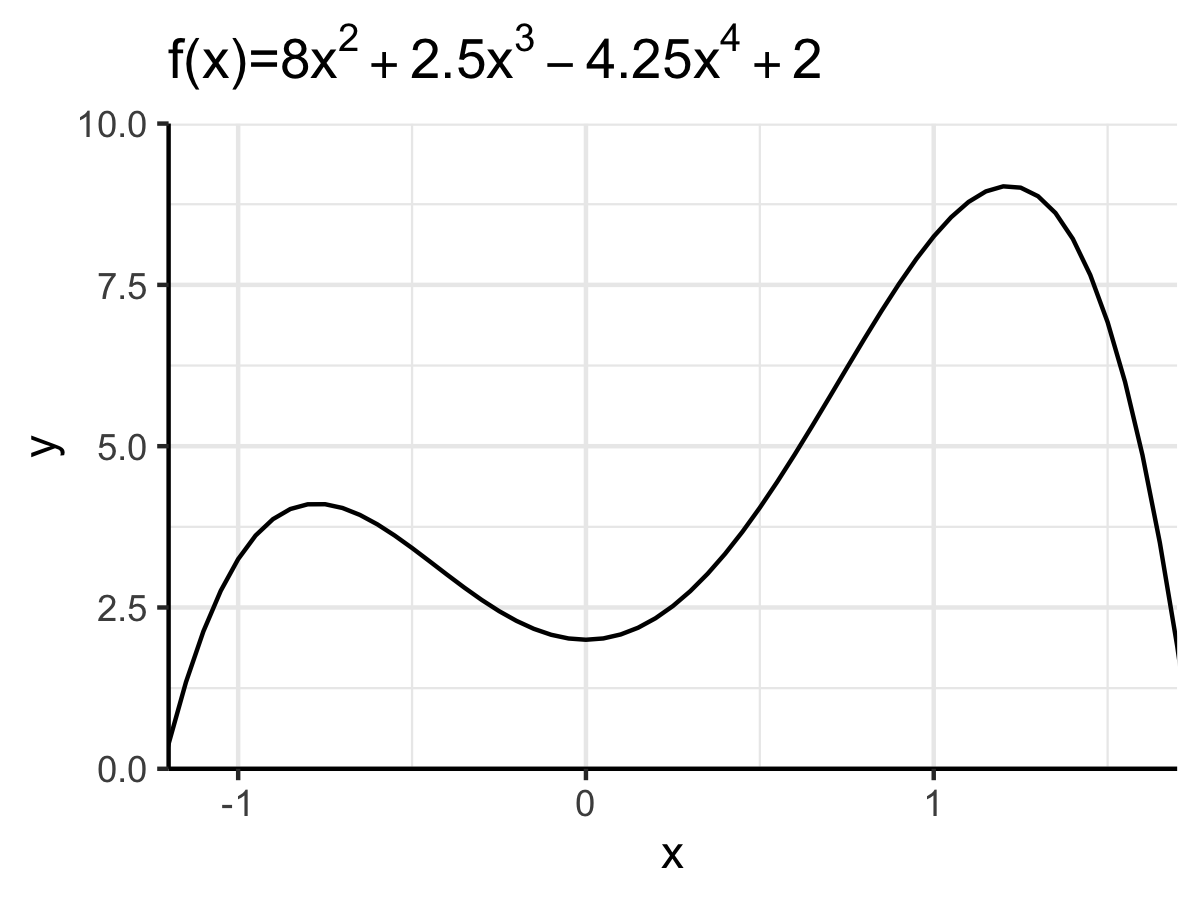
Abbildung 6.6: Graph der zu optimierenden Funktion.

Da es sich hier um ein eindimensionales Problem handelt, können wir die allgemeine Funktion optimize() verwenden. Wir übergeben als Argument f die zu optimierende Funktion und geben über interval das Intervall an, in dem nach einem Minimum (oder Maximum) gesucht werden soll:

opt_obj <- optimize(f = f_1, interval = c(-1.25, 1.75))
opt_obj

#> $minimum
#> [1] -7.54766e-06
#> 
#> $objective
#> [1] 2

Das Ergebnis ist eine Liste mit zwei Elementen. Dem x-Wert des gesuchten Minimums:⁴⁹

opt_obj[["minimum"]]

#> [1] -7.54766e-06

Und dem dazugehörigen Funktionswert:

opt_obj[["objective"]]

#> [1] 2

Falls wir ein Maximum suchen setzen wir maximum=TRUE:

opt_obj_max <- optimize(
  f = f_1, interval = c(-1.25, 1.75), maximum = TRUE)
opt_obj_max

#> $maximum
#> [1] 1.215492
#> 
#> $objective
#> [1] 9.032067

Falls wir den Suchbereich entsprechend einschränken finden wir das lokale Maximum auf der linken Seite:

opt_obj_max <- optimize(
  f = f_1, interval = c(-1.25, 0), maximum = TRUE)
opt_obj_max

#> $maximum
#> [1] -0.7743199
#> 
#> $objective
#> [1] 4.108106

Wir sind übrigens nicht auf eindimensionale Funktionen beschränkt. Wir können z.B. auch die folgende Zielfunktion optimieren:

\[f(x,y)=(a-x)^2 + b(y-x^2)^2\]

f_2 <- function(x, a=1, b=100){
  (a - x[1])**2 + b*(x[2]-x[1]**2)**2
}

Bei dieser Funktion handelt es sich um die in der Optimierung sehr häufig als Benchmark verwendete Rosenbrock Funktion. Grafisch können wir solche Funktionen mit Hilfe einer Heatmap darstellen, wobei wir in unserer Visualisierung in Abbildung 6.7 annehmen, dass \(a=1\) und \(b=100\). In einer Heatmap geben die beiden Achsen die Kombination der x und y-Werte an, der resultierende Funktionswert wird über die Farbe repräsentiert.

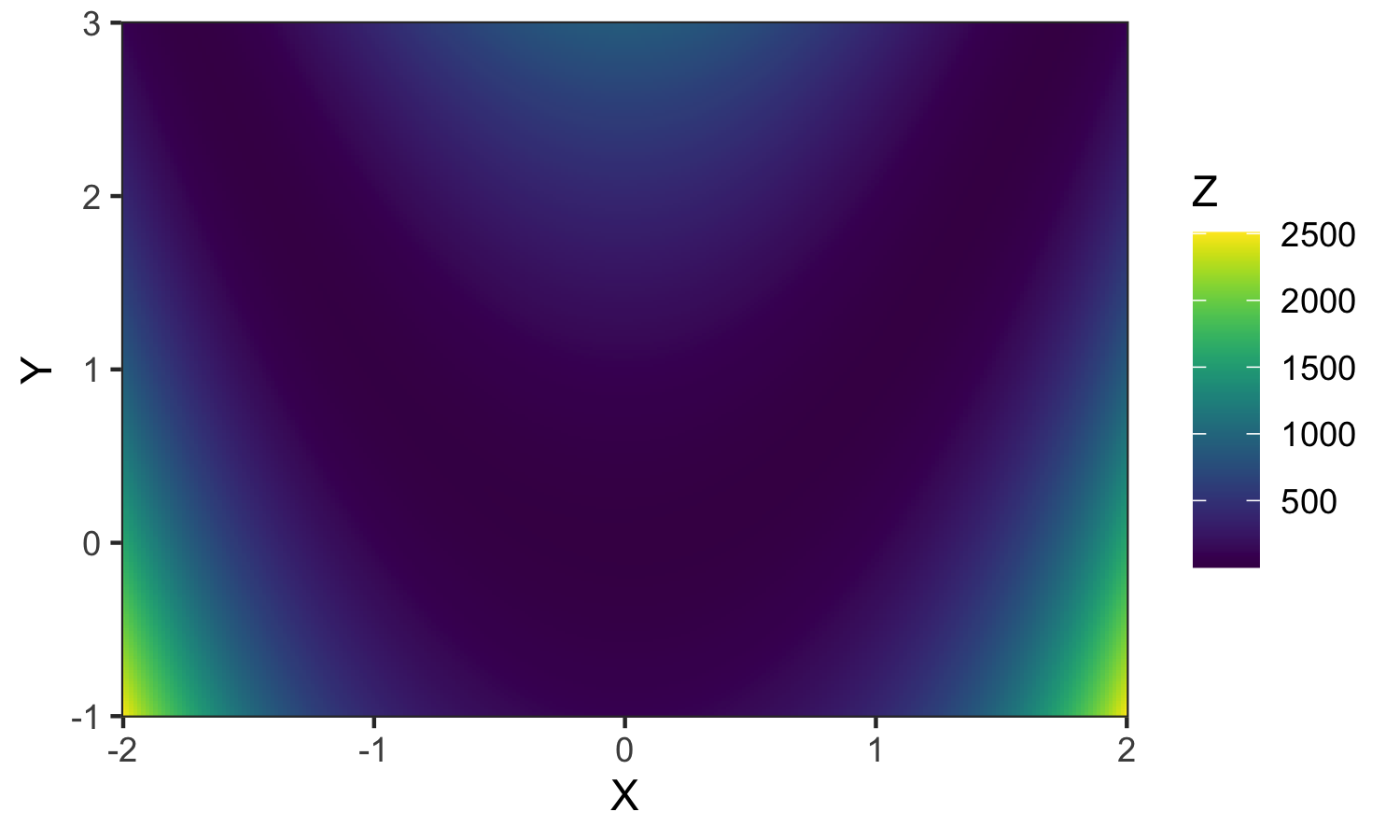
Abbildung 6.7: Darstellung einer Funktion als Heatmap

Da es sich jetzt um ein mehrdimensionales Problem handelt verwenden wir die Funktion optimx::optimr() anstatt von optimize(). Die Handhabung ist aber sehr ähnlich. Als erstes Argument übergeben wir par unsere ersten Vermutungen für das Extremum, also die Werte, mit der die Funktion ihre Suche beginnen soll. Danach als zweites Argument fn die zu optmierende Funktion. Falls diese Funktion noch weitere Argumente akzeptiert können wir die hier auch einfach hinzufügen. Für unseren Fall haben wir also:

opt_objekt <- optimx::optimr(
  par = c(1, 1),
  fn = f_2
  )

Zunächst schauen wir ob der Algorithmus erfolgreich einen Extremwert gefunden hat. Bei erfolgreicher Suche hat der Listeneintrag convergence den Wert 0:

opt_objekt[["convergence"]] == 0 

#> [1] TRUE

Die optimalen Argumente erhalten wir über den Listeneintrag par:

opt_objekt[["par"]]

#> [1] 1 1

Und den Wert der Zielfunktion im Extremum über den Listeneintrag value:

opt_objekt[["value"]]

#> [1] 0

Wenn wir optimx::optimr() übrigens zur Maximierung einsetzen wollen müssen wir nichts weiter tun als dem Argument control eine Liste mit dem Eintrag fnscale=-1 zu übergeben:

opt_objekt <- optimx::optimr(
  par = c(1, 1),
  fn = f_2, control = list(fnscale=-1)
  )

opt_objekt$convergence == 0

#> [1] TRUE

opt_objekt$par

#> [1]  3.661667e+76 -3.087043e+76

opt_objekt$value

#> [1] 1.797693e+308

6.2.6 Anwendungsbeispiel

Als Anwendungsbeispiel betrachten wir das klassische keynesianische Modell. Am geläufigsten ist dabei folgende Formulierung:

\[\begin{align} Y&=C+I+G\\ C&=c_0+c_1 Y \end{align}\]

In dem Modell geht man davon aus, dass sich die gesamtwirtschaftliche Güternachfrage \(Y\) aus dem Konsum \(C\), den Investitionen \(I\) sowie den Staatsausgaben \(G\) ergibt. Die Konsumfunktion selbst wird als lineare Funktion modelliert, wobei \(c_0\) den autonomen Konsum (also den vom Einkommen unabhängigen Konsum) und \(c_1\) die marginale Konsumquote beschreibt.

Wir können nun die Notation leicht um \(T\) als die Steuerlast erweitern:

\[\begin{align} Y=\frac{c_0 + I + G}{1-c_1(1-T)} \end{align}\]

Wenn wir nun wissen wollen wie \(Y\) auf eine Änderung der Staatsausgaben reagiert können wir diese Formel nach \(G\) ableiten. Dazu müssten wir gleich mehrere Regeln, die wir oben kennen gelernt haben, anwenden.

Aber natürlich können wir das Ganze ganz einfach in R lösen. Um die Ableitung herzuleiten verwenden wir dabei einfach wieder die Funktion D():

keynes_model <- expression(Y=(c_0 + I + G) / (1 - c_1*(1-T)))
D(expr = keynes_model, name = "G")

#> 1/(1 - c_1 * (1 - T))

Es gilt also:

\[\begin{align} \frac{\partial Y}{\partial G} &= \frac{1}{1-c_1(1-T)} \end{align}\]

Nehmen wir einmal an die marginale Konsumquote \(c_1\) läge bei \(20\%\) und der Steuersatz \(T\) bei \(25\%\). Eine Erhöhung der Staatsausgaben würde dann \(Y\) über den Multiplikator \(\frac{1}{1-0.2(1-0.25)}=1.176471\) erhöhen.

Alternativ können wir das Ergebnis natürlich analytisch unter Zuhilfenahme der oben eingeführten Ableitungsregeln herleiten.

6.3 Lineare Algebra

Ebenfalls sehr häufig werden Sie mit Matrizen und den dazugehörigen Rechenoperationen (‘Matrizenalgebra’ genannt) in Kontakt kommen. Das Ziel dieses Abschnitts ist keine abschließende Einführung in Matrizen und Matrizenalgebra, sondern soll dazu dienen, einen groben Überblick über typische Rechenoperationen und deren Implementierung in R zu bekommen. Für eine ausführlichere Einführung verweisen wir auf Wainwright und Chiang (2005) oder Aleskerov, Ersel, und Piontkovski (2011).

Matrizen werden häufig im Kontext der linearen Algebra verwendet.⁵⁰ Zahlreiche sozioökonomische Konzepte bedienen sich der linearen Algebra, in der Matrizen häufig verwendet werden, um lineare Gleichungssysteme dazustellen. Die Matrixdarstellung ist dabei nicht nur kompakter, sie erlaubt es uns auch relativ leicht zu überprüfen ob das System konsistent und lösbar ist. Die foldenden zwei Beispiele machen dies hoffentlich deutlich.

6.3.1 Einführungsbeispiele

Das erste Beispiel bezieht sich wieder auf das oben eingeführte klassischen Keynesianische Modell:

\[\begin{align} Y&=C+I+G\\ C&=c_0+c_1Y \end{align}\]

Nehmen wir nun an, die Staatsausgaben und Investitionen wären exogen bekannt. Dann kann dieses Modell äquivalent in Matrixform geschrieben werden:

\[\begin{align} Ax = d \end{align}\] wobei \(A=\left(\begin{array}{cc} 1 & -1 \\ -c_1 & 1 \end{array}\right)\), \(x=\left(\begin{array}{cc} Y \\ C \end{array}\right)\) und \(d=\left(\begin{array}{cc} I + G \\ c_0 \end{array}\right)\), wobei die beiden Unbekannten in diesem Fall das Einkommen \(Y\) und der Konsum \(C\) sind.

Matrizen helfen uns solche Gleichungssysteme komprimiert darzustellen und zu analysieren, insbesondere um zu testen ob es Werte für die freien Parameter - hier \(Y\) und \(C\) - gibt sodass das gesamte System konsistent ist. Wir sehen unten wie genau wir solche Systeme in R recht einfach lösen können.

Ein weiteres Beispiel wo wir - vielleicht auch häufig unbewusst - Methoden der linearen Algebra verwenden ist in der Ökonometrie. So wird das einfache lineare Regressionsmodell für \(n\) Beochatungen und \(p\) erklärenden Variablen häufig folgendermaßen beschrieben (siehe Kapitel 10):

\[\begin{align} Y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + ... + \beta_p x_{ip} + \epsilon, i=1,...,n \end{align}\]

Da wir in der Praxis regelmäßig mehr als eine erklärende Variable verwenden (also \(p>1\)) werden Schätzgleichungen fast ausschließlich in Matrixform dargestellt, denn wir können explizit alle \(n\) Gleichungen untereinander schreiben:

\[\begin{align} Y_1 = \beta_0 + \beta_1 x_{11} + \beta_2 x_{12} + ... + \beta_p x_{1p} + e_1\nonumber\\ Y_2 = \beta_0 + \beta_1 x_{21} + \beta_2 x_{22} + ... + \beta_p x_{2p} + e_2\nonumber\\ \vdots \nonumber\\ Y_n = \beta_0 + \beta_1 x_{n1} + \beta_2 x_{n2} + ... + \beta_p x_{np} + e_n\nonumber \end{align}\]

Und dann in Matrixform ausdrücken:

\[\begin{align} \left( \begin{array}{c} Y_1 \\ Y_2 \\ \vdots\\ Y_n\\ \end{array} \right) = \left( \begin{array}{ccccc} 1 & x_{11} & x_{12} & \dots & x_{1p} \\ 1 & x_{21} & x_{22} & \dots & x_{2p} \\ \vdots & \vdots & \vdots & \vdots & \vdots\\ 1 & x_{n1} & x_{n2} & \dots & x_{np} \\ \end{array} \right) \times \left( \begin{array}{c} \beta_0 \\ \beta_1 \\ \vdots\\ \beta_n\\ \end{array} \right) + \left( \begin{array}{c} \epsilon_1 \\ \epsilon_2 \\ \vdots\\ \epsilon_n\\ \end{array} \right) \end{align}\]

Und Letzteres wie folgt schreiben:

\[\begin{align} \boldsymbol{Y} = \boldsymbol{X\beta} + \boldsymbol{\epsilon} \end{align}\]

Dementsprechend können wir auch den OLS-Schätzer in Matrixform darstellen, was ab Kapitel 11 auch die standardmäßige Darstellungsform sein wird. Dies erlaubt einfachere und allgemeinere Beweise, und ist vor allem für die algorithmische Implementierung sehr wichtig. Auch wenn wir uns mit diesen Details nicht notwendigerweise genau auseinandersetzen müssen, sollte die grundlegende Rolle der linearen Algebra doch nicht unterschätzt werden. Wir werden das Beispiel des OLS-Schätzers unten noch genauer besprechen. Zunächst beginnen wir mit einer allgemeinen Einführung in den Umgang mit Matrizen in R.

6.3.2 Einführung von Matrizen

Technisch handelt es sich bei Matrizen um zweidimensionale Objekte mit Zeilen und Spalten, bei denen es sich jeweils um atomare Vektoren handelt.

In R werden Matrizen mit der Funktion matrix()erstellt. Diese Funktion nimmt als erstes Argument die Elemente der Matrix und dann die Spezifikation der Anzahl von Zeilen (nrow) und/oder der Anzahl von Spalten (ncol):

m_1 <- matrix(11:20, nrow = 5)
m_1

#>      [,1] [,2]
#> [1,]   11   16
#> [2,]   12   17
#> [3,]   13   18
#> [4,]   14   19
#> [5,]   15   20

Wie können die Zeilen, Spalten und einzelne Werte folgendermaßen extrahieren und ggf. Ersetzungen vornehmen:

m_1[,1] # Erste Spalte

#> [1] 11 12 13 14 15

m_1[1,] # Erste Zeile

#> [1] 11 16

m_1[2,2] # Element [2,2]

#> [1] 17

Es gibt einige besondere Matrizen, die aufgrund ihrer speziellen Eigenschaften Eigennamen erhalten haben.

Eine Matrix mit der gleichen Anzahl von Zeilen und Spalten wird quadratische Matrix genannt.

\[\begin{align} \left( \begin{array}{cccc} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \\ \end{array} \right) \end{align}\]

Die Elemente auf der ‘Diagonalen’ einer quadratischen \(n\times n\)-Matrix, also \(\{a_ii\}^n_{i=1}\), werden die Hauptdiagonale dieser Matrix genannt.

Eine Matrix, die von Null verschiedene Einträge nur auf der Hauptdiagonale aufweist heißt Diagonalmatrix:

\[\begin{align} \left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 \\ 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & 4 \\ \end{array} \right) \end{align}\]

Bei der oberen Dreiecksmatrix befinden sich von Null verschiedene Einträge ausschließlich auf oder über der Hauptdiagonale, bei der unteren Dreiecksmatrix ist dies genau umgekehrt. Hier ein Beispiel für eine untere Dreiecksmatrix:

\[\begin{align} \left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 1 & 2 & 0 & 0 \\ 1 & 2 & 3 & 0 \\ 1 & 2 & 3 & 4 \\ \end{array} \right) \end{align}\]

Bei der Identitätsmatrix (oder: ‘Einheitsmatrix’) handelt es sich um eine quadratische Matrix, die auf der Hauptdiagonalen nur 1er und neben der Haupdiagonalen nur 0er enthält. Sie wird mit \(\mathbb{I_n}\) bezeichnet, wobei \(n\) die Anzahl der Zeilen und Spalten angibt:

\[\begin{align} \mathbb{I_4}= \left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} \right) \end{align}\]

Wird eine beliebige Matrix mit einer passenden Identitätsmatrix multipliziert, ist das Ergebnis die ursprüngliche Matrix selbst, daher der Name. Wir können \(\mathbb{I}_n\) in R mit diag(n) direkt erstellen.

6.3.3 Grundregeln der Matrizenalgebra

Matrizenalgebra spielt in vielen statistischen Anwendungen eine wichtige Rolle. Sie funktioniert aber ein wenig anders als die ‘herkömmliche’ Algebra, mit denen die meisten von Ihnen schon vertraut sein werden. Zum Glück ist es in R sehr einfach die typischen Rechenoperationen für Matrizen zu implementieren. Im Folgenden werden wir die wichtigsten Rechenregeln für Matrizen kurz einführen und dabei die folgenden Beispielmatrizen verwenden:

\[\begin{align} A = \left( \begin{array}{rrr} 1 & 6 \\ 5 & 3 \\ \end{array} \right) \quad B = \left( \begin{array}{rrr} 0 & 2 \\ 4 & 8 \\ \end{array}\right) \end{align}\]

matrix_a <- matrix(c(1,5,6,3), ncol = 2)
matrix_b <- matrix(c(0,4,2,8), ncol = 2)

Matrix-Transponierung

Die transponierte Matrix \(A'\) ergibt sich aus \(A\) indem die Spalten und Zeilen vertauscht werden. Im Folgenden ist unsere Beispielmatrix und ihre Transponierung dargestellt:

\[\begin{align} A = \left( \begin{array}{rrr} 1 & 6 \\ 5 & 3 \\ \end{array} \right) \quad A' = \left( \begin{array}{rrr} 1 & 5 \\ 6 & 3 \\ \end{array} \right) \end{align}\]

In R können wir eine Matrix mit der Funktion t() transponieren:

matrix_a

#>      [,1] [,2]
#> [1,]    1    6
#> [2,]    5    3

t(matrix_a)

#>      [,1] [,2]
#> [1,]    1    5
#> [2,]    6    3

Skalar-Addition

\[\begin{align} 4+\boldsymbol{A}= \left( \begin{array}{rrr} 4+a_{11} & 4+a_{21} \\ 4+a_{12} & 4+a_{22} \\ \end{array} \right) \end{align}\]

In R:

4 + matrix_a

#>      [,1] [,2]
#> [1,]    5   10
#> [2,]    9    7

Matrizen-Addition

\[\begin{align} \boldsymbol{A}+\boldsymbol{B}= \left( \begin{array}{rrr} a_{11} + b_{11} & a_{21} + b_{21}\\ a_{12} + b_{12} & a_{22} + b_{22}\\ \end{array} \right) \end{align}\]

matrix_a + matrix_b

#>      [,1] [,2]
#> [1,]    1    8
#> [2,]    9   11

Skalar-Multiplikation

\[\begin{align} 2\cdot\boldsymbol{A}= \left( \begin{array}{rrr} 2\cdot a_{11} & 2\cdot a_{21} \\ 2\cdot a_{12} & 2\cdot a_{22} \\ \end{array} \right) \end{align}\]

2*matrix_a

#>      [,1] [,2]
#> [1,]    2   12
#> [2,]   10    6

Elementenweise Matrix Multiplikation (auch ‘Hadamard-Produkt’)

\[\begin{align} \boldsymbol{A}\odot\boldsymbol{B}= \left( \begin{array}{rrr} a_{11}\cdot b_{11} & a_{21}\cdot b_{21}\\ a_{12}\cdot b_{12} & a_{22}\cdot b_{22}\\ \end{array} \right) \end{align}\]

matrix_a * matrix_b

#>      [,1] [,2]
#> [1,]    0   12
#> [2,]   20   24

Matrizen-Multiplikation \[\begin{align} \boldsymbol{A}\cdot\boldsymbol{B}= \left( \begin{array}{rrr} a_{11}\cdot b_{11} + a_{12}\cdot b_{21} & a_{11}\cdot b_{21}+a_{12}\cdot b_{22}\\ a_{21}\cdot b_{11} + a_{22}\cdot b_{21} & a_{21}\cdot b_{12}+a_{22}\cdot b_{22}\\ \end{array} \right) \end{align}\]

matrix_a %*% matrix_b

#>      [,1] [,2]
#> [1,]   24   50
#> [2,]   12   34

Wir wissen von oben auch, dass \(A\mathbb{I}_2=A\):

matrix_a

#>      [,1] [,2]
#> [1,]    1    6
#> [2,]    5    3

matrix_a %*% diag(2)

#>      [,1] [,2]
#> [1,]    1    6
#> [2,]    5    3

Matrizen invertieren

Die Inverse einer Matrix \(\boldsymbol{A}\), \(\boldsymbol{A}^{-1}\), ist definiert sodass gilt

\[\begin{align} \boldsymbol{A}\boldsymbol{A}^{-1}=\boldsymbol{I} \end{align}\]

Sie kann in R mit der Funktion inv() aus dem Paket matlib⁵¹ identifiziert werden, wobei wir die Matrix als erstes Argument X an inv() übergeben:

inv(X = matrix_a)

#>            [,1]        [,2]
#> [1,] -0.1111111  0.22222222
#> [2,]  0.1851852 -0.03703704

matrix_a %*% inv(matrix_a)

#>       [,1]   [,2]
#> [1,] 1e+00 -2e-08
#> [2,] 2e-08  1e+00

Die minimalen Abweichungen sind auf machinelle Rundungsfehler zurückzuführen und treten häufig auf.

Gerade die letzte Operation ist zentral um zu verstehen wie wir mit Hilfe der Matrizenalgebra lineare Gleichungssysteme wie oben beschrieben lösen können. Denn diese Gleichungssysteme können - wie in der Einleitung beschrieben - in die Form

\[\begin{align} Ax=b \end{align}\]

gebracht werden. In Anwendungsfällen ist \(A\) eine Matrix mit Koeffizienten, \(x\) ein Vektor von unbekannten Variablen und \(b\) ein Vektor mit Konstanten. Entsprechend ist unser Interesse in der Identifikation eines Vektors \(x\) sodass die Gleichung konsistent ist und mindestens eine Lösung hat. Wenn wir die Gleichung gemäß der gerade beschriebenen Regeln umformen bekommen wir:

\[\begin{align} A^{-1}Ax &= A^{-1}b\\ x &= A^{-1}b \end{align}\]

In der Matrizenschreibweise korrespondiert die Lösung eines solchen Systems also zur Invertierung der Matrix \(A\) - daher auch der Name der R-Funktion solve() aus dem Paket base.

Nehmen wir also einmal folgenden Fall an: \(A=\left(\begin{array}{cc} 1 & 3 \\ -2 & 1 \end{array}\right)\) und \(b=\left(\begin{array}{c} 9 \\ 4 \end{array}\right)\).

In diesem Fall können wir das Gleichungssystem in R lösen indem wir Solve() direkt die Matrix \(A\) (über das Argument A) und den Vektor \(b\) (über das Argument b) übergeben:

A <- matrix(c(1, -2, 3, 1), ncol = 2)
b <- matrix(c(9, -4), ncol = 1)
Solve(A = A, b = b)

#> x1    =  3 
#>   x2  =  2

Wir sehen also unmittelbar, dass das Gleichungssystem - und damit unser Modell - konsistent ist und eine eindeutige Lösung \(x=\left(\begin{array}{c} 3 \\ 2 \end{array}\right)\) aufweist.⁵² Dieses können wir folgendermaßen verifizieren:

x <- matrix(c(3, 2), ncol = 1)
A %*% x

#>      [,1]
#> [1,]    9
#> [2,]   -4

Wie erwartet erhalten wir hier also wieder unseren ursprünglichen Wert für \(b\).

Wenn allerdings \(A=\left(\begin{array}{cc} -2 & 1 \\ -4 & 2 \end{array}\right)\) und \(b=\left(\begin{array}{c} 3 \\ 2 \end{array}\right)\), dann würde Folgendes passieren:

A <- matrix(c(-2, -4, 1, 2), ncol = 2)
b <- matrix(c(3, 2), ncol = 1)
Solve(A = A, b = b)

#> x1 - 0.5*x2  =  -0.5 
#>           0  =     2

Wir sehen also direkt, dass das System nicht lösbar wäre, denn das resultierende Gleichungssystem weist einen eindeutigen Widerspruch (0=2) auf. Der Grund ist, dass die Matrix \(A\) singulär ist, das heißt sie besitzt keine Inverse. Das können Sie unmittelbar überprüfen:

inv(A)

#> Error in Inverse(X, tol = sqrt(.Machine$double.eps), ...): X is numerically singular

Wir können also nur über die Analyse der Matrix Schlussfolgerungen bezüglich des gesamten Gleichungssystems ziehen. Das ist in der Praxis, in dem die Gleichungssysteme ungleich größer und komplexer sind, von enormer Bedeutung.

Ein dritter möglicher Fall tritt ein wenn \(A=\left(\begin{array}{cc} 1 & 3 \\ -2 & 1 \end{array}\right)\) und \(b=\left(\begin{array}{c} 9 \\ 4 \end{array}\right)\):

A <- matrix(c(4, -2, -2, 1), ncol = 2)
b <- matrix(c(6, -3), ncol = 1)
Solve(A = A, b = b)

#> x1 - 0.5*x2  =  1.5 
#>           0  =    0

In diesem Falle sehen wir keinen Widerspruch im Gleichungssystem, aber auch kein eindeutiges Ergebnis. Das Gleichungssystem hat also unendlich viele Lösungen.

Zur Vollständigkeit seien hier noch einmal die drei möglichen Ergebnisse einer solchen Matrizenanalyse kurz beschrieben:

1. Das Gleichungssystem hat unendlich viele Lösungen, wir können also auf Basis der Struktur keine genaue Vorhersage bezüglich der Parameter in \(x\) machen.

2. Das Gleichungssystem hat eine eindeutige Lösung, wir haben also ein konsistentes Modell, das eine eindeutige Vorhersage produziert.

3. Das Gleichungssystem hat keine Lösung, unser Modell ist also inkonsistent.

Im Folgenden werden wir uns das anhand der beiden Beispiele aus dem Abschnitt 6.3.1 genauer anschauen.

6.3.4 Anwendungsbeispiel 1: Das einfache Keynesianische Modell

In der Einleitung dieses Unterkapitels haben wir schon gesehen, dass wir das einfache Keynesianische Modell

\[\begin{align} Y&=C+I+G\\ C&=a+bY \end{align}\]

auch in Matrizenschreibweise darstellen können:

\[\begin{align} Ax = d \end{align}\] wobei \(A=\left(\begin{array}{cc} 1 & -1 \\ -b & 1 \end{array}\right)\), \(x=\left(\begin{array}{cc} Y \\ C \end{array}\right)\) und \(d=\left(\begin{array}{cc} I + G \\ a \end{array}\right)\).

Der Vorteil ist, dass wir unmittelbar überprüfen können ob das System für bestimmte Werte konsistent ist und eine eindeutige Lösung für \(Y\) und \(C\) besitzt.

Sind z.B. die Staatsausgaben mit \(G=2\) und die Investitionen mit \(I=2\) bekannt, und die marginale Konsumneigung mit \(b=0.4\) und der einkommensunabhängige Konsum mit \(a=1\) gegeben, können wir direkt überprüfen ob das System konsistent ist und, da \(x=\left(\begin{array}{cc} Y \\ C \end{array}\right)\) welche Werte für den Konsum und das Gesamteinkommen impliziert werden.

I_keynes <- 2
G_keynes <- 2
b_keynes <- 0.4
a_keynes <- 1

A_keynes <- matrix(c(1, -b_keynes, -1, 1), nrow = 2)
d_keynes <- matrix(c(I_keynes + G_keynes, a_keynes), ncol = 1)
Solve(A = A_keynes, b = d_keynes)

#> x1    =  8.33333333 
#>   x2  =  4.33333333

In diesem Fall sehen wir, dass das System konsistent ist und eine eindeutige Lösung für das Einkommen \(Y=8\frac{1}{3}\) und den Konsum \(C=4\frac{1}{3}\) impliziert.

6.3.5 Anwendungsbeispiel 2: OLS-Regression

Aus der Einleitung dieses Unterkapitels wissen wir, dass wir das lineare Regressionsmodell mit \(n\) Beobachtungen von \(p\) Variablen

\[\begin{align} Y_1 = \beta_0 + \beta_1 x_{11} + \beta_2 x_{12} + ... + \beta_p x_{1p} + \epsilon_1\nonumber\\ Y_2 = \beta_0 + \beta_1 x_{21} + \beta_2 x_{22} + ... + \beta_p x_{2p} + \epsilon_2\nonumber\\ \vdots \nonumber\\ Y_n = \beta_0 + \beta_1 x_{n1} + \beta_2 x_{n2} + ... + \beta_p x_{np} + \epsilon_n\nonumber \end{align}\]

auch folgendermaßen schreiben können:

\[\begin{align} \boldsymbol{Y} = \boldsymbol{X\beta} + \boldsymbol{\epsilon} \end{align}\]

Wobei \(\boldsymbol{Y}\) eine \(n\times 1\)-Matrix mit den Beobachtungen für die abhängige Variable, \(\boldsymbol{X}\) eine \(n\times p\)-Matrix in der jede Spalte zu einem Vektor mit allen \(n\) Beobachtungen einer der \(p\) erklärenden Variablen korrespondiert. \(\boldsymbol{\epsilon}\) schließlich ist die \(n\times 1\)-Matrix der Fehlerterme.

Nehmen wir folgenden Datensatz an:

#>              Auto Verbrauch  PS Zylinder
#> 1: Ford Pantera L      15.8 264        8
#> 2:   Ferrari Dino      19.7 175        6
#> 3:  Maserati Bora      15.0 335        8
#> 4:     Volvo 142E      21.4 109        4

Dies können wir schreiben als:

\[\begin{align} y_1 = \beta_0 + \beta_1 x_{11} + \beta_2 x_{12} + \epsilon_{1} \nonumber\\ y_1 = \beta_0 + \beta_1 x_{21} + \beta_2 x_{32} + \epsilon_{2} \nonumber\\ y_1 = \beta_0 + \beta_1 x_{31} + \beta_2 x_{32} + \epsilon_{3} \nonumber\\ y_1 = \beta_0 + \beta_1 x_{41} + \beta_2 x_{42} + \epsilon_{4} \nonumber\\ \end{align}\]

und mit Zahlen:

\[\begin{align} 15.8 = \beta_0 + \beta_1 264 + \beta_2 8 + \epsilon_{1} \nonumber\\ 19.7 = \beta_0 + \beta_1 175 + \beta_2 6 + \epsilon_{2} \nonumber\\ 15.0 = \beta_0 + \beta_1 335 + \beta_2 8 + \epsilon_{3} \nonumber\\ 21.4 = \beta_0 + \beta_1 109 + \beta_2 4 + \epsilon_{4} \nonumber\\ \end{align}\]

Und als Matrix:

\[\begin{align} \left(\begin{array}{ccc} 1 & 264 & 8 \\ 1 & 175 & 6 \\ 1 & 335 & 8 \\ 1 & 109 & 4 \end{array}\right) \times \left(\begin{array}{cc} \beta_0 \\ \beta_1 \\ \beta_2 \end{array}\right) + \left(\begin{array}{c}\epsilon_{1} \\ \epsilon_{2} \\ \epsilon_{3} \\ \epsilon_{4} \end{array}\right) &= \left(\begin{array}{c} 15.8 \\ 19.7 \\ 15.0 \\ 21.4 \end{array}\right)\nonumber \end{align}\]

Es gilt also, dass \(\boldsymbol{\hat{\beta}}=\left(\begin{array}{cc} \hat{\beta}_0 \\ \hat{\beta}_1 \\ \hat{\beta}_2 \end{array}\right)\), \(\boldsymbol{X}=\left(\begin{array}{ccc} 1 & 264 & 8 \\ 1 & 175 & 6 \\ 1 & 335 & 8 \\ 1 & 109 & 4 \end{array}\right)\) und \(\boldsymbol{y}=\left(\begin{array}{c} 15.8 \\ 19.7 \\ 15.0 \\ 21.4 \end{array}\right)\).

Es lässt sich allgemein zeigen, dass der gesuchte Schätzer \(\boldsymbol{\hat{\beta}}=\left(\begin{array}{cc} \hat{\beta}_0 \\ \hat{\beta}_1 \\ \hat{\beta}_2 \end{array}\right)\) für das unbekannte \(\boldsymbol{\beta}=\left(\begin{array}{cc} \beta_0 \\ \beta_1 \\ \beta_2 \end{array}\right)\) die Lösung des folgenden Gleichungssystems darstellt:⁵³

\[\begin{align} \boldsymbol{\hat{\beta}}=\left(\boldsymbol{X}'\boldsymbol{X} \right)^{-1}\boldsymbol{X}'\boldsymbol{Y} \end{align}\]

Das können wir wiederum in R lösen:

ols_X <- matrix(c(1, 264, 8, 1, 175, 6, 1, 335, 8, 1, 109, 4), 
                ncol = 3, byrow = T)
ols_y <- matrix(c(15.8, 19.7, 15.0, 21.4), ncol = 1)

solve(t(ols_X) %*% ols_X) %*% t(ols_X) %*% ols_y

#>             [,1]
#> [1,] 26.37086491
#> [2,] -0.01783627
#> [3,] -0.68592421

Oder direkt mit lm():

lm(Verbrauch~PS+Zylinder, data = ols_beispiel)

#> 
#> Call:
#> lm(formula = Verbrauch ~ PS + Zylinder, data = ols_beispiel)
#> 
#> Coefficients:
#> (Intercept)           PS     Zylinder  
#>    26.37086     -0.01784     -0.68592

6.3.6 Optional: Herleitung des OLS-Schätzers

Mit dem bislang gewonnenen Verständnis von Matrizenalgebra ist es bereits möglich die Herleitung des OLS-Schätzers nachzuvollziehen. Diese Herleitung wird im Folgenden beschrieben.

Wir wissen bereits, dass die Residuen einer Schätzung gegeben sind durch:

\[\boldsymbol{e}=\boldsymbol{Y}-\boldsymbol{X\hat{\beta}}\]

Wir können die Summe der quadrierten Residuen (RSS) in Matrixschreibweise schreiben als:

\[\begin{align} \boldsymbol{e'e}= \left(\begin{array}{cccc} e_1 & e_2 & ... & e_n \end{array}\right) \left(\begin{array}{cc} e_1 \\ e_2 \\ \vdots \\ e_n \end{array}\right) =\left(\begin{array}{cccc} e_1\times e_1 & e_2 \times e_2 & ... & e_n \times e_n \end{array}\right) \end{align}\]

Wir können dann schreiben:⁵⁴

\[\begin{align} \boldsymbol{e'e} &= \left(\boldsymbol{Y}-\boldsymbol{X\hat{\beta}}\right)' \left(\boldsymbol{Y}-\boldsymbol{X\hat{\beta}}\right)\nonumber\\ &=\boldsymbol{y'y}-\boldsymbol{\hat{\beta}'X'y}-\boldsymbol{y'X\hat{\beta}} + \boldsymbol{\hat{\beta}'X'X\hat{\beta}}\nonumber\\ &=\boldsymbol{y'y}-2\boldsymbol{\hat{\beta}X'y}+ \boldsymbol{\hat{\beta}'X'X\hat{\beta}}\nonumber \end{align}\]

Wir wollen diesen Ausdruck nun minimieren. Dazu leiten wir nach dem Vektor der zu schätzenden Koeffizienten \(\boldsymbol{\hat{\beta}}\) ab:

\[\begin{align} \frac{\partial \boldsymbol{e'e}}{\partial\boldsymbol{\hat{\beta}}}= -2\boldsymbol{X'y} + 2\boldsymbol{X'X\hat{\beta}} = 0 \end{align}\]

Diese Gleichung können wir nun umformen zu:

\[\begin{align} 2\boldsymbol{X'X\hat{\beta}} &= 2\boldsymbol{X'Y}\nonumber\\ \boldsymbol{X'X\hat{\beta}}&=\boldsymbol{X'Y}\nonumber \end{align}\]

Da gilt, dass \(\left(\boldsymbol{X'X}\right)^{-1}\left(\boldsymbol{X'X}\right)=I\) multiplizieren wir beide Seiten mit \(\left(\boldsymbol{X'X}\right)^{-1}\):⁵⁵

\[\begin{align} \left(\boldsymbol{X'X}\right)^{-1}\boldsymbol{X'X\hat{\beta}} &= \left(\boldsymbol{X'X}\right)^{-1}\boldsymbol{X'Y}\nonumber\\ \boldsymbol{\hat{\beta}} &= \left(\boldsymbol{X'X}\right)^{-1}\left(\boldsymbol{X'Y}\right) \end{align}\]

Damit haben wir den Schätzer für \(\boldsymbol{\hat{\beta}}\) hergeleitet.

6.3.7 Weiterführende Literatur

Es gibt im Internet zahlreiche gute Überblicksartikel zum Thema Matrizenalgebra in R, z.B. hier oder in größerem Umfang hier. Auch das Angebot an Lehrbüchern ist sehr groß, für die ökonomischen Grundlagen bietet sich Wainwright und Chiang (2005) sehr gut an.

6.4 Analyse von Verteilungen

Fragen nach Verteilungen stehen im Zentrum vieler sozioökonomischer Arbeiten. Verteilung von Einkommen und Vermögen, sozialem, kulturellem oder physischem Kapital, Firmenproduktivitäten oder natürlichen Ressourcen - in vielen Bereichen geht es Verteilungen.

Gleichzeitig spielen Verteilungen in der technischen Literatur eine wichtige Rolle: in der Ökonometrie ist die Verteilung von Schätzern von zentraler Bedeutung, viele formale Konzepte setzen eine bestimmte Verteilung der Daten voraus und häufig bedarf es zur richtigen Wahl der quantitativen Methoden zumindest rudimentärer Kenntnis über die Verteilung die Daten.

Kurzum: Wissen über Verteilungen und deren Analyse ist für die sozioökonomische Forschungspraxis extrem hilfreich. Daher wollen wir uns im Folgenden mit verschiedenen Aspekten der Analyse von Verteilungen beschäftigen.

Wir steigen mit einer Erläuterung des (mathematischen) Verteilungsbegriffs ein und diskutieren den Zusammenhang zwischen Verteilungen und stochastischen Prozessen. Verteilungen sind nämlich immer dann zentral, wenn wir es mit probabilistischen Prozessen zu tun haben.

Als nächstes lernen wir typische Kennzahlen zur Beschreibung von Verteilungen kennen. Besonderes Augenmerk legen wir dabei auf Kennzahlen zur Streuung und Ungleichheit, wie die Standardabweichung oder den Gini Index.

Daraufhin lernen wir einige grafische Methoden kennen, um die wir die quantitativen Kennzahlen immer ergänzen sollten und schließen das Kapitel zuletzt mit einigen abschließenden Bemerkungen ab.

In diesem Abschnitt werden mehrere Konzepte aus der Stochastik vorausgesetzt. Wenn Sie sich damit noch unsicher fühlen empfiehlt sich vorher eine Lektüre von Kapitel 7.

6.4.1 Theoretische und empirische Verteilungen

Wenn wir über Verteilungen sprechen wird der Begriff (mindestens) in zwei verwandten aber unterschiedlichen Arten verwendet: im Sinne der Verteilung einer Zufallsvariablen und im Sinne einer empirischen Beschreibung.

Eine empirische Verteilung beschreiben wir in der Regel durch bestimmte Kennzahlen, wie den Mittelwert, die Standardabweichung oder den Gini-Index. Das erlaubt uns Informationen über die Daten in wenigen Zahlen zu kondensieren.⁵⁶

Dennoch werden beide Perspektiven auch häufig kombiniert, vor allem wenn wir einen empirischen Datensatz mit einem parametrischen Wahrscheinlichkeitsmodell beschreiben wollen. Das bedeutet, dass wir die empirischen Daten als Realisierung einer theoretischen Zufallsvariablen (ZV) interpretieren und die für die theoretische ZV relevanten Parameter dann aus den Daten heraus schätzen.⁵⁷

Anwendungsbeispiel

Stellen Sie sich vor Sie haben eine Stichprobe vor sich, welche die Verteilung in Abbildung 6.8 (linker Graph) aufweist.

Beachten Sie, dass die y-Achse die empirische Dichte der Beobachtungen auf der x-Achse angibt, wir haben hier also ein Maß für die relative Häufigkeit der Beobachtungen. Dies haben wir mit der Funktion ggplot2::stat(density) innerhalb von ggplot2::geom_histogram() erreicht.

Wenn wir die Daten so betrachten erscheint es naheliegend, sie als Realisierung einer Normalverteilung zu interpretieren: die Form ist grob glockenförmig und symmetrisch. Wir können diese Annahme plausibilisieren indem wir mit ggplot2::geom_density() die empirische Dichtefunktion der Verteilung schätzen und über die Daten legen, wie im rechten Graph der Abbildung 6.8.

Stichprobe <- ggplot2::ggplot(data = sample_data) +
  ggplot2::geom_histogram(
    mapping = aes(x=r, stat(density)), 
    binwidth = 0.4) +
  ggplot2::scale_x_continuous(expand = c(0, 1)) + 
  ggplot2::scale_y_continuous(
    expand = expansion(c(0, 0.05), c(0, 0)), name = "Dichte") +
  ggplot2::theme_bw() + 
  theme(panel.border = element_blank(), 
        axis.line = element_line(),
        axis.title.x = element_blank())

Dichtefunktion <- ggplot2::ggplot(data = sample_data) +
  ggplot2::geom_histogram(
    mapping = aes(x=r, stat(density)), 
    binwidth = 0.4, alpha=0.4) +
    coord_cartesian(xlim = c(-6, 12)) +
  ggplot2::stat_density(mapping = aes(x=r), 
               color="blue", 
               geom="line") +
  ggplot2::scale_y_continuous(
    expand = expansion(c(0, 0.05), c(0, 0)), name = "Dichte") +
  ggplot2::theme_bw() + 
  theme(panel.border = element_blank(), 
        axis.line = element_line(),
        axis.title.x = element_blank())

dichte_plot <- ggpubr::ggarrange(Stichprobe, Dichtefunktion, ncol = 2)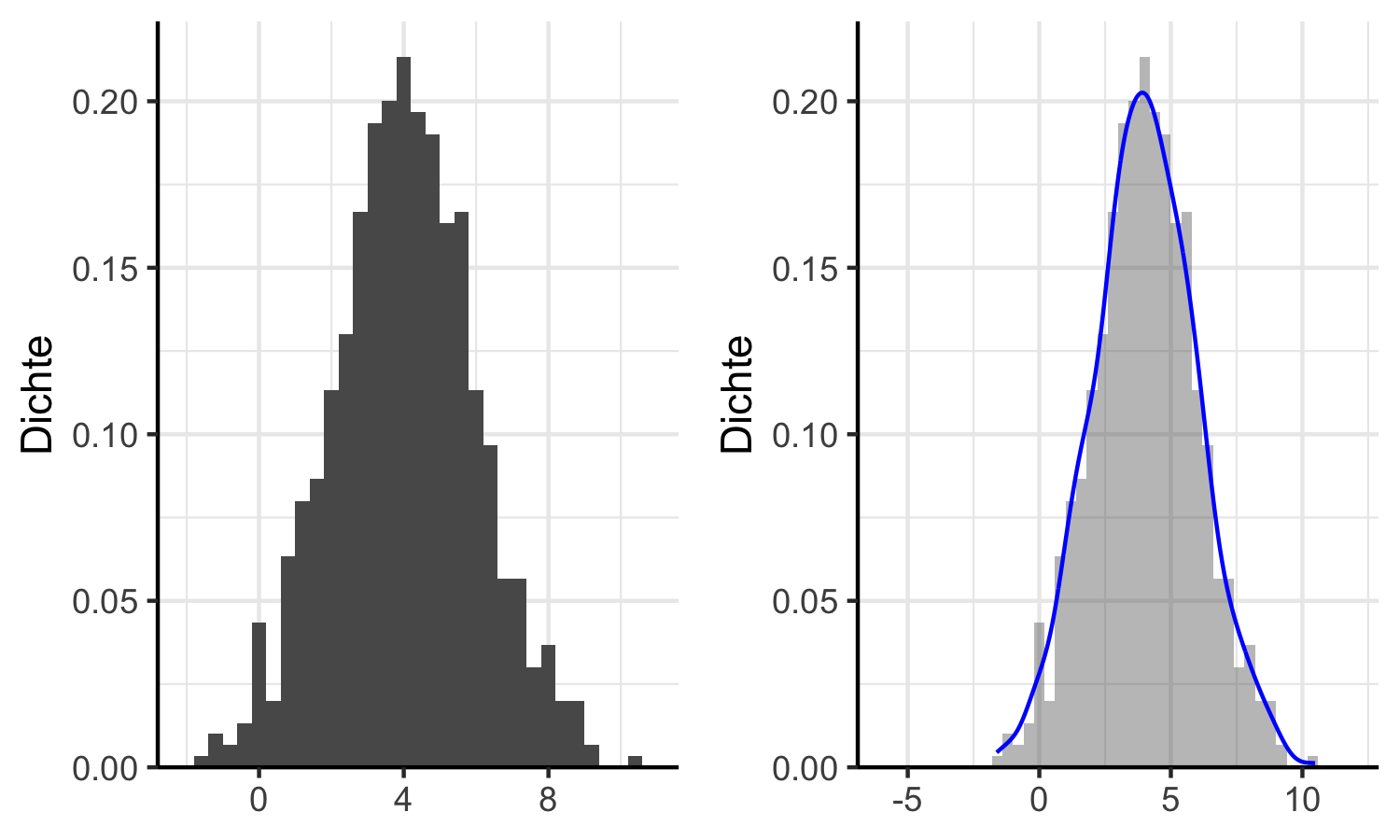

Abbildung 6.8: Stichprobe (linker Graph) und Stichprobe mit empirischer Dichtefunktion (rechter Graph)

Das bedeutet, dass wir unsere Daten mit Hilfe der Dichtefunktion (probability density function - PDF) der Normalverteilung beschreiben können. Die Formel an sich ist dabei weniger illustrativ, aber sie zeigt was wir mit einem parametrischen Wahrscheinlichkeitsmodell meinen:

\[\begin{align} f(x)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} \end{align}\]

Wenn Sie die Formel genau anschauen finden sich darin zwei Parameter: ein Lageparameter \(\mu\) und ein Streuparameter \(\sigma^2\). Das bedeutet, dass wir mit diesen beiden Werten die theoretische Normalverteilung vollständig charakterisieren können. Es wäre ja schön, wenn wir unsere Stichprobe oben ebenfalls mit solchen zwei Zahlen vollständig beschreiben könnten.

Das geht allerdings nicht. Unsere empirisch erhobenen Daten sind nie komplett identisch zu einer theoretischen Verteilung. Was wir daher machen können ist Folgendes: wir argumentieren, dass unsere Daten sinnvoll durch eine normalverteilte ZV modelliert werden können. Wir sagen dann, dass unsere Stichprobe approximativ normalverteilt ist. Dann müssen wir im nächsten Schritt nur noch die Werte für die beiden Parameter der Normalverteilung finden, sodass die Verteilung optimal zu unseren Daten passt. Das bedeutet wir ‘fitten’ die Verteilung zu unseren Daten. Abbildung 6.9 verdeutlicht die Fits verschiedener Normalverteilungen.

Was damit gemeint ist verdeutlicht die folgende Darstellung:

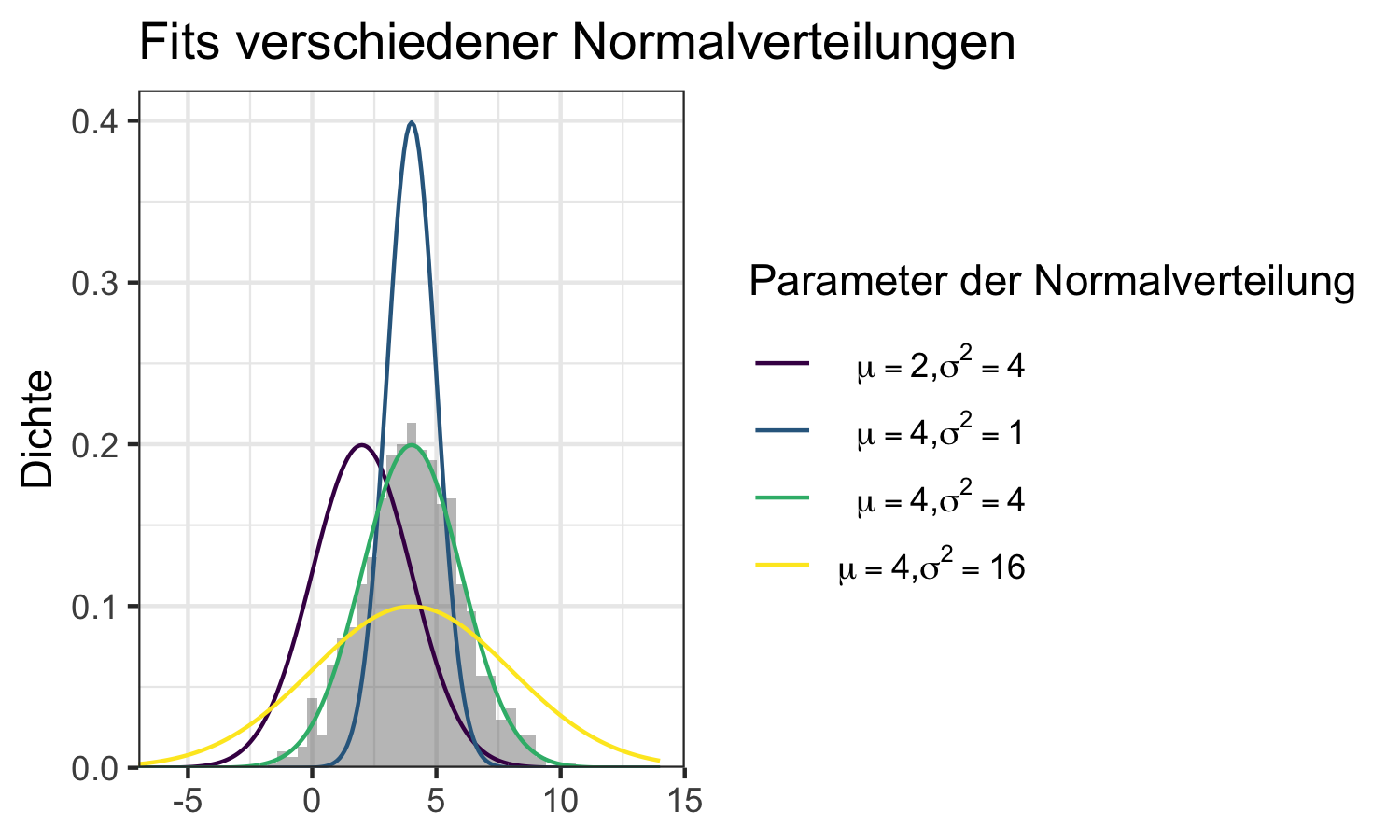
Abbildung 6.9: Beispiel zur Verdeutlichung von Fits verschiedener Normalverteilungen mit unterschiedlichen Parameterwerten

Die Normalverteilung mit \(\mu=4\) und \(\sigma^2=4\) passt zu den Daten recht gut. Aber wie identifizieren wir diese Werte? In der Praxis müssen diese Werte geschätzt werden. Dazu gibt es verschiedene Verfahren.

Die bekannteste Variante ist die Maximum Likelihood Schätzung. Das Verfahren wird später genauer beschrieben, hier illustrieren wir es mit unserem aktuellen Beispiel.

Die Grundidee der Maximum Likelihood-Schätzung ist simpel: wählen Sie die Parameter der Verteilung so, dass die beobachtete Stichprobe die am wahrscheinlichsten zu beobachtende Stichprobe ist. In unserem Falle: wählen Sie \(\mu=\mu^*\) und \(\sigma^2=\sigma^{2*}\) so, dass \(\mathcal{N}(\mu^*, \sigma^{2*})\), die Normalverteilung ist, bei der die Wahrscheinlichkeit unsere Stichprobe zu bekommen am größten ist.

Bedenken Sie, dass das nichts darüber aussagt wie wahrscheinlich das ist: wenn Sie eine unpassende Verteilung mit Maximum Likelihood fitten, bekommen Sie selbst für die besten Parameter einen schlechten Fit.

In unserem Fall wollen wir nun eine Normalverteilung zu unseren Daten fitten. Dazu verwenden wir die Funktion fitdist() aus dem Paket fitdistrplus (Delignette-Muller und Dutang 2015). Dieser Funktion geben wir über das Argument data unsere Stichprobe und über das Argument distr das Kürzel für die Verteilungsklasse, die wir annehmen.⁵⁸

fit_dist <- fitdistrplus::fitdist(data = sample_data$r, 
                    distr = "norm")
fit_dist[["estimate"]]

#>     mean       sd 
#> 4.023254 1.967130

Wir sehen also, dass die optimale Parametrisierung zu \(\mu=4.02\) und \(\sigma^2=1.967\) korrespondiert. Das passt gut zu unserem grafischen Resultat von oben, bei dem uns \(\mathcal{N}(4,2)\) bereits als guter Fit ins Auge gesprungen ist.

Allerdings müssten Sie zusätzlich noch testen ob die Verteilungsannahme auch tatsächlich plausibel ist, wir testen also die Hypothese, dass die Daten aus einer \(\mathcal{N}(4,2)\)-Verteilung gezogen wurden. Für den Fall der Normalverteilung können wir dies z.B. mit einem Shapiro-Wilk-Test machen.

Hier testen wir die \(H_0\), dass die Daten tatsächlich durch eine Normalverteilung generiert wurden.⁵⁹

shapiro_test <- shapiro.test(sample_data$r)
shapiro_test

#> 
#>  Shapiro-Wilk normality test
#> 
#> data:  sample_data$r
#> W = 0.99894, p-value = 0.9479

Da der \(p>0.1\) können wir die Nullhypothese einer Normalverteilung nicht ablehnen und wir können nun ein gutes Bild unserer Daten vermitteln: wann immer Sie hören, dass ein bestimmter Datensatz approximativ gemäß \(\mathcal{N}(4,2)\) verteilt ist, dann haben Sie ein sehr gutes Bild des Datensatzes erhalten.

Es gibt viele verschiedene Verteilungstests, je nach dem welche Verteilung Sie testen wollen. Dies ist ein komplexes Thema, das wir in diesem Kapitel nicht weitergehend behandeln. Clauset, Shalizi, und Newman (2009) ist ein sehr bekanntest Paper, das eine praktische Anleitung für den Fall der Pareto-Verteilung enthält, aber auch für andere Verteilungen verwendet werden kann.⁶⁰ Ansonsten finden Sie hier oder hier praktische Anleitungen und Diskussionen.

6.4.2 Kennzahlen zur Beschreibung empirischer Verteilungen

Jede Beschreibung einer Verteilung mittels Kennzahlen sollte verschiedene Aspekte der Verteilung abdecken. Insbesondere sollten Aussagen zu Lage, zur Streuung, zur Form und zu möglichen Ausreißern und zu sonstigen Besonderheiten gemacht werden. Tabelle 6.3 listet die bekanntesten Kennzahlen in den jeweiligen Bereichen auf.

Tabelle 6.3: Kennzahlen zur Beschreibung empirischer Verteilungen.

Kennzahl	Art	R-Funktion
Arithm. Mittel	Lage	mean()
Modus	Lage	NA
Median	Lage	median()
Quantile	Lage	quantile()
Varianz	Streuung	var()
Standardabweichung	Streuung	sd()
Variationskoeffizient	Streuung	sd()/mean()
IQR	Streuung	IQR()
Gini	Streuung	ineq::Gini()
Theil	Streuung	ineq::Theil()
Schiefe	Form	moments::skewness()
Steile	Form	moments::kurtosis()
Cook’sche Distanz	Sonst.	cooks.distance()

Für die folgenden Illustrationen nehmen wir an, dass wir es mit einem Datensatz mit \(N\) kontinuiertlichen Beobachtungen \(x_1, x_2, ..., x_n\) zu tun haben. Als Beispiel dient uns der Datensatz zu ökonomischen Journalen aus Kleiber und Zeileis (2008):⁶¹

#>    Kuerzel                                               Titel
#> 1:    APEL                   Asian-Pacific Economic Literature
#> 2:  SAJoEH           South African Journal of Economic History
#> 3:      CE                             Computational Economics
#> 4:  MEPiTE MOCT-MOST Economic Policy in Transitional Economics
#> 5:    JoSE                          Journal of Socio-Economics
#> 6:   LabEc                                    Labour Economics
#>                    Verlag Society Preis Seitenanzahl Buchstaben_pS Zitationen
#> 1:              Blackwell      no   123          440          3822         21
#> 2: So Afr ec history assn      no    20          309          1782         22
#> 3:                 Kluwer      no   443          567          2924         22
#> 4:                 Kluwer      no   276          520          3234         22
#> 5:               Elsevier      no   295          791          3024         24
#> 6:               Elsevier      no   344          609          2967         24
#>    Gruendung Abonnenten           Bereich
#> 1:      1986         14           General
#> 2:      1986         59  Economic History
#> 3:      1987         17       Specialized
#> 4:      1991          2      Area Studies
#> 5:      1972         96 Interdisciplinary
#> 6:      1994         15             Labor

Kennzahlen zur Lage der Verteilung

Die bekannteste Maßzahl zur Lage einer Verteilung ist das arithmetische Mittel. Es ist anwendbar wenn wir es mit kontinuierlichen und mindestens intervall-skalierten Daten zu tun haben und ist definiert als:

\[\bar{x}=\frac{1}{N}\sum_{i=1}^Nx_i\]

In R wird das arithmetische Mittel mit der Funktion mean() berechnet:

avg_preis <- mean(journal_daten[["Preis"]])
avg_preis

#> [1] 417.7222

Der durchschnittliche Preis der Journale ist also 417.72 Dollar.

Das arithmetische Mittel ist sehr anfällig gegenüber Ausreißern. Ein robusteres Maß ist der Median: er ist definiert als der Wert \(x_{0.5}\) bei dem 50% der Daten größer und 50% der Daten kleiner sind als \(x_{0.5}\), genauer:

\[\begin{align} x_{0.5} = \begin{cases} \frac{1}{2} \left(x_{0.5\cdot n} + x_{0.5\cdot n + 1}\right) & \text{wenn } 0.5 \cdot x\text{ ganzzahlig}\\ \frac{1}{2} x_{\lfloor 0.5\cdot n + 1\rfloor} & \text{wenn } 0.5 \cdot x\text{ nicht ganzzahlig}\\ \end{cases} \end{align}\]

wobei wir annehmen, dass die Werte der Verteilung ihrer Größe nach geordnet sind, also \((x_1\leq x_2\leq x_3 \leq...\leq x_n)\) und \(\lfloor x \rfloor\) die Abrundungsfunktion bezeichnet.⁶²

In R wird der Median mit der Funktion median() berechnet:

med_preis <- median(journal_daten[["Preis"]])
med_preis

#> [1] 282

Da es insgesamt 180 Journale gibt gilt, dass 90 Journale teurer und 90 Journale billiger als 282 Dollar sind.

Die Idee des Medians kann über den Begriff der Quantile verallgemeinert werden. Wir sprechen bei dem \(\alpha\)-Quantil einer Verteilung von dem Wert, bei dem \(\alpha\cdot 100\%\) der Datenwerte kleiner und \((1-\alpha)\cdot 100\%\) der Datenwerte größer sind. Genauer:

\[\begin{align} x_{\alpha} = \begin{cases} \frac{1}{2} \left(x_{\alpha\cdot n} + x_{\alpha5\cdot n + 1}\right) & \text{wenn } \alpha \cdot x ganzzahlig\\ \frac{1}{2} x_{\lfloor \alpha\cdot n + 1\rfloor} & \text{wenn } \alpha \cdot x nicht ganzzahlig\\ \end{cases} \end{align}\]

In R können wir Quantile einfach mit der Funktion quantile() berechnen. Diese Funktion akzeptiert als erstes Argument einen Vektor von Daten und als zweites Argument ein oder mehrere Werte für \(\alpha\):

quantile(journal_daten[["Preis"]], c(0.25, 0.5, 0.75))

#>    25%    50%    75% 
#> 134.50 282.00 540.75

Wie wir hier sehen ist der Median gleich dem \(50\%\)-Quantil.

Eine sehr flexible Kennzahl für die Lage einer Verteilung ist der Modus. Er bezeichnet den Wert, der am häufigsten in den Daten vorkommt. Daher ist der Modus auch schon für nominal-skalierte Daten verfügbar.

In R gibt es aber leider keine Funktion, die den Modus direkt berechnet. Vielleicht erinnern Sie sich aber, dass wir mit der Funktion table() eine Häufigkeitstabelle ausgeben können. Daher bekommen wir den Modus über folgenden Umweg:⁶³

names(table(journal_daten[["Preis"]])
      )[table(journal_daten[["Preis"]])==max(table(journal_daten[["Preis"]]))]

#> [1] "90"

Kennzahlen zur Streuung einer Verteilung

Von besonderem Interesse in der sozioökonomischen Forschung ist die Analyse von Ungleichheiten. Dies bedeutet, dass Kennzahlen zur Beschreibung der Streuung von Verteilungen von besonderer praktischer Bedeutung sind.

Die am weitesten verbreiteten Streuungsmaße sind die Varianz \(Var\) und ihre Quadratwurzel, die Standardabweichung, \(s\):

\[\begin{align} s_x=\sqrt{Var(x)}=\sqrt{\frac{1}{N-1}\sum_{i=1}^N\left(x_i-\bar{x}\right)^2} \end{align}\]

Dabei ist zu beachten, dass die empirische Standardabweichung oft einfacher zu interpretieren ist, da sie in den gleichen Einheiten gemessen wird wie die Daten der Stichprobe. Der Variationskoeffizient ist eine einheitslose Variante und ist als Quotient der empirische Standardabweichung und dem arithmetischen Mittel definitiert:

\[\begin{align} v_x=\frac{s_x}{\bar{x}} \end{align}\]

In R können die drei Maße folgendermaßen berechnet werden:

var_preis <- var(journal_daten[["Preis"]])
var_preis

#> [1] 148868.3

sd_preis <- sd(journal_daten[["Preis"]])
sd_preis

#> [1] 385.8346

varcoef_preis <- sd(journal_daten[["Preis"]]) / mean(journal_daten[["Preis"]])
varcoef_preis

#> [1] 0.9236631

Ein ebenfalls häufig verwendetes Streuungsmaß ist der Interquantilsabstand (*inter-quantile-range, IQR), welcher als die Differenz zwischen dem \(25\%-\) und \(75\%-\)Quantil definiert ist:

\[IQR=x_{0.75} - x_{0.25}\]

Hierbei handelt es sich also um das Intervall, das die ‘mittlere Hälfte’ der Verteilung umfasst. In R können wir den IQR mit der Funktion IQR berechnen:

IQR(journal_daten[["Preis"]])

#> [1] 406.25

Ein weit verbreitetes Maß zur Messung der Streuung ist der Gini-Index. Dabei handelt es sich um ein relatives Verteilungsmaß, welches auf das Intervall \((0,1)\) normiert wird und den Wert 0 im Falle einer kompletten Gleichverteilung und den Wert 1 im Falle eine kompletten Konzentration, d.h. dem Fall, dass ein Beobachtungssubjekt alles und alle anderen nichts besitzen.

In R können wir den Gini-Index z.B. mit der Funktion Gini() aus dem Paket ineq (Zeileis 2014) berechnen, wobei wir hier die Korrektur für Stichproben verwenden müssen indem wir das Argument corr = TRUE setzen:

test_data_equality <- rep(0.5, 5)
test_data_inequality <- c(rep(0, 4), 1)
ineq::Gini(test_data_equality, corr = T)

#> [1] 0

ineq::Gini(test_data_inequality, corr = T)

#> [1] 1

Um die Besonderheiten des Gini’s zu verstehen wollen wir uns genauer mit der Berechnung des Indexes vertraut machen. Der Gini-Index ist eng mit dem Konzept der Lorenz-Kurve verknüpft.

Grafisch gesprochen resultiert die Lorenz-Kurve wenn wir auf der x-Achse den Anteil der Beobachtungssubjekte und auf der y-Achse ihren Anteil an den relevanten Ressource abbilden. Definieren wir \(p\) als den Anteil an der Population und \(q=\mathcal{L}(p)\) als den Anteil an der Ressource, der von \(p\%\) der Population gehalten wird. Daraus resultiert, dass wir bei völliger Gleichverteilung eine Gerade sehen würden, da \(p\%\) der Population auch \(q=p=\mathcal{L}(p)\%\) der Ressource halten würden. Die Lorenz-Kurve visualisiert nun die Abweichung von diesem idealtypischen Fall in dem \(p=q\). Dies wird in Abbildung 6.10 deutlich, in der zwei mögliche Lorenz-Kurven dem hypothetischen Fall der perfekten Gleichverteilung gegenübergestellt werden:

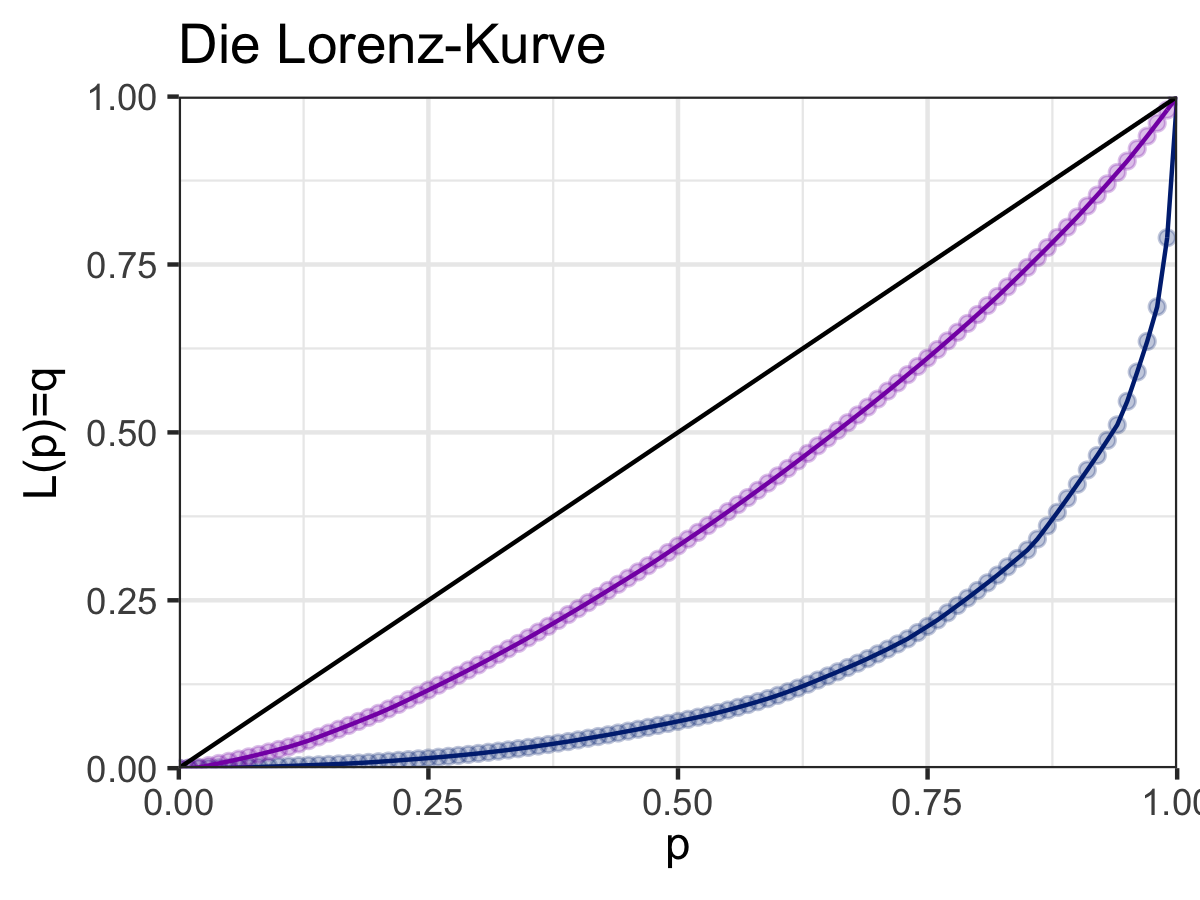
Abbildung 6.10: Vergleich zweier Lorenz-Kurven

Der Gini-Index \(\mathcal{G}\) misst diese Abweichung über die normierte Distanz zwischen \(p\) und \(q\) indem er einfach das Integral von \(p-\mathcal{L}(p)\) berechnet. Da die Lorenz-Kurve innerhalb eines \(1\times 1\)-Quadrats definiert ist mutliplizieren wir das Integral mit 2 um die Normierung zwischen 0 und 1 zu erreichen, sonst wäre das Maximum des Gini-Indices 0.5 (da über der 45-Grad Linie per definitionem keine Kurve verlaufen kann):

\[\begin{align} \mathcal{G}= 2\cdot \int_0^1\left(p-\mathcal{L}\left(p\right)\right)\text{d}p = 1-2\cdot \int_0^1\left(\mathcal{L}\left(p\right)\right)\text{d}p \end{align}\]

Der Gini-Index ist ein recht hilfreiches Maß für Ungleichverteilung wenn wir es mit symmetrischen Verteilungen zu tun haben, wie die lila Kurve in der Abbildung oben. Es ist jedoch ein schwierigeres Maß sobald eine assymmetrische Verteilung vorliegt, wie bei der blauen Kurve oben. In letzterem Fall werden wir möglicherweise die gleichen Ginis für recht unterschiedliche Verteilungen erhalten. Da Vermögens- und Einkommensverteilungen in der Regel immer asymmetrisch sind stellt das durchaus eine Herausforderung für den Gini dar und man sollte andere Ungleichheitsmaße wie den Atkinson-Index oder den Zanardi-Index in Betracht ziehen.

Der Gini-Index reagiert relativ schwach auf Änderungen an den Extremen der Ressourcenverteilung. Wenn diese Änderungen von besonderem Interesse sind bietet sich die Verwendung des Theil-Index an. Er ist leider nicht so einfach zu interpretieren wie der Gini und eignet sich daher vor allem für Vergleiche über die Zeit.^[Der Theil-Index besitzt noch weitere attraktivere Eigenschaften. Insbesondere können die Beiträge von Ungleichheiten innerhalb verschiedener Subgruppen und die Ungleichheiten zwischen Gruppen als solchen aus dem Index abgeleitet werden.

Die Definition ist folgendermaßen:

\[\begin{align} \mathcal{T}= \frac{1}{N}\sum_{i=1}^N\frac{x_i}{\bar{x}}\ln\frac{x_i}{\bar{x}} \end{align}\]

wobei \(N\) die Anzahl der Personen, \(x_i\) die Ressourcenausstattung von Person \(i\) und \(\bar{x}\) das arithmetische Mittel der Ressourcenausstattung ist.

In R können wir den Theil Index mit der Funktion Theil() aus dem Paket ineq berechnen:

dist_expl <- rpareto(100, 3, 2.1)
ineq::Theil(dist_expl)

#> [1] 1.290735

Welches Verteilungsmaß für den jeweiligen Anwendungsfall am besten geeignet ist hängt auch von der Art der zugrundeliegenden Verteilung ab. So wird zwar häufig die Varianz als Streuungsmaß verwendet, wenn es sich bei der zu analysierenden Verteilung allerdings um eine bei Einkommen sehr häufig vorkommende Pareto-Verteilung handelt ist die Verwendung dieses Maßes ziemlich irreführend, da die Varianz für diese Verteilungen in vielen Fällen nicht sinnvoll definiert werden kann und wir mit der Formel für die Varianz indirekt unsere Stichprobengröße messen (Yang u. a. 2019). Das richtige Maß hängt also immer von unseren theoretischen Vorüberlegungen zur zugrundeliegenden Verteilung und unserem konkreten Erkenntnisinteresse ab.

In diesem Sinne ist vor allem die weite Verbreitung des Gini-Indexes als dem Verteilungsmaß schlechthin durchaus kritisch zu sehen. So reagiert der Gini-Index vor allem auf Änderungen in den mittleren Bereichen der Verteilung und weniger auf Änderungen an den Rändern. Wer Effekte von wachsender Vermögenskonzentration bei den reichsten Individuen messen möchte sollte also lieber ein anderes Maß verwenden. Sein Nutzen ist insofern auch von der zugrundeliegenden Forschungsfrage abhängig. Das gilt natürlich auch für alle anderen Indices. So eignet sich der Theil-Index vor allem bei der Analyse von Änderungen über die Zeit in der gleichen Gruppe, da er nicht normiert ist. Er reagiert deutlich besser auf Änderungen an den Extremen als der Gini-Index.

Für eine gute kritische Auseinandersetzung mit dem Gini-Index und einen konstruktiven Gegenvorschlag siehe z.B. Clementi u. a. (2019).

Zahlreiche gängige Verteilungsmaße sind in dem Paket ineq von Zeileis (2014) implementiert.

Uni- und Multimodale Verteilungen

Die Unterscheidung zwischen uni- und multimodalen Verteilungen ist wichtig, weil viele Kennzahlen, wie die Schiefe oder Steile einer Verteilung (siehe unten) nur für unimodale Verteilungen intuitiv interpretiert werden können.

Ganz strikt genommen sprechen wir von einer unimodalen oder eingipfligen Verteilung wenn Sie nur einen Gipfel hat, also nur einen Modus Ansonsten sprechen wir von einer multimodalen oder mehrgipfligen (oder genauer zweigipfligen, dreigipfligen, …) Verteilung.

In der Praxis haben viele Funktionen einen eindeutigen Modus, besitzen aber mehrere andere lokale Optima, also kleinere “Gipfel”, sodass wir in der Regel von einer multimodalen Verteilung sprechen sobald es mehrere lokale Maxima gibt. Beispiele einer solch multimodalen Verteilung sind in Abbildung 6.11 dargestellt.

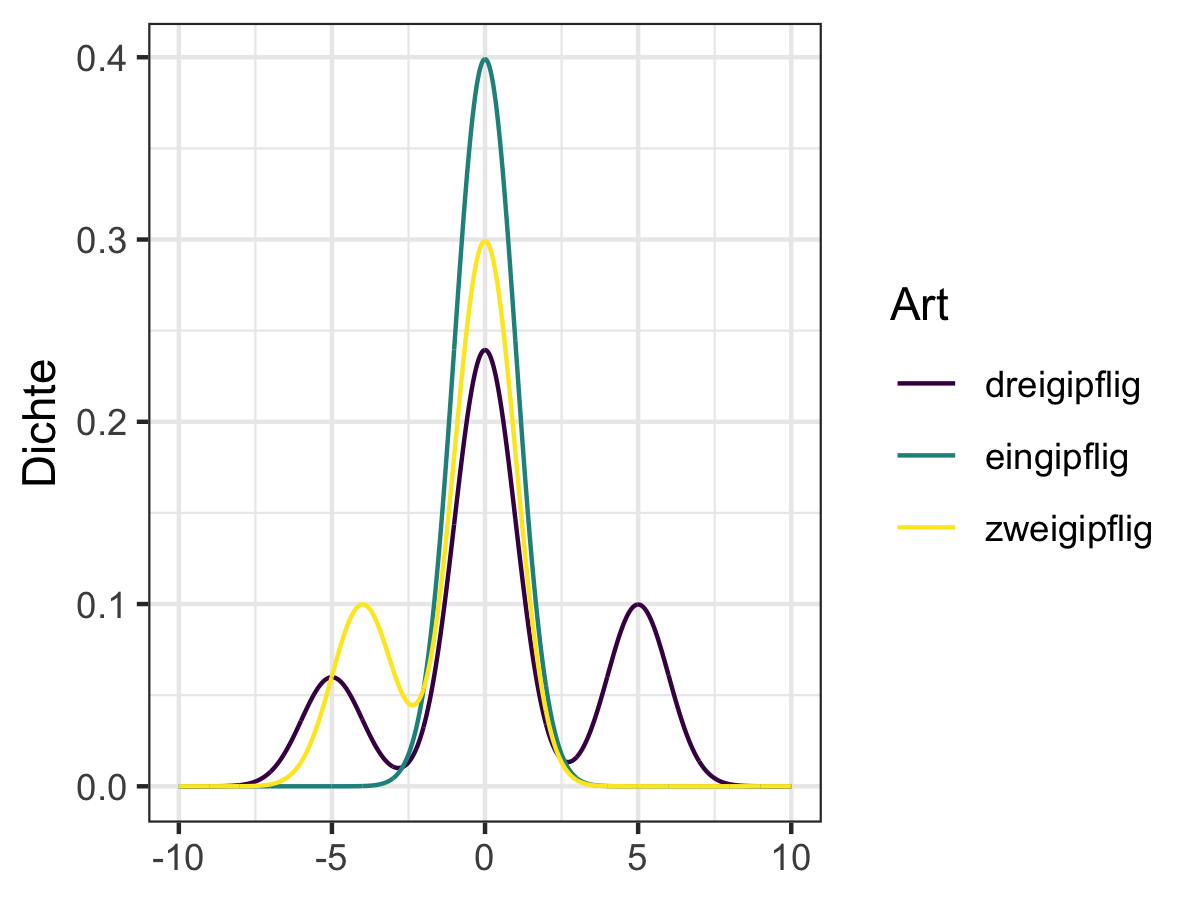
Abbildung 6.11: Beispiele multimodaler Verteilungen

Kennzahlen zur Form der Verteilung

Um die Form einer Verteilung besser zu beschreiben verwendet man häufig die Schiefe und Steile (auch: Kurtosis) einer Verteilung. Beide Kennzahlen sind zunächst einmal nur für eingipflige/unimodale Verteilungen sinnvoll.

Die Schiefe einer empirischen Verteilung ist definiert als:

\[\gamma_x = \frac{1}{n}\sum_{i=1}^n\left(\frac{x_i-\bar{x}}{s}\right)^3\]

wobei wir für die Schätzung wieder für die Reduktion der Freiheitsgrade korrigieren müssen, sodass die praktische Schätzfunktion gegeben ist durch:

\[\hat{\gamma_x} = \frac{1}{(n-1)(n-2)}\sum_{i=1}^n\left(\frac{x_i-\bar{x}}{s}\right)^3\]

Hieraus ableiten können wir den Begriff der Symmetrie einer Verteilung. Wir nennen eine Verteilung symmetrisch wenn \(\gamma_x=0\), links-schief (oder rechts-steil) wenn \(\gamma_x<0\) und rechts-schief (oder links-steil) wenn \(\gamma_x>0\).

Woher diese Begriffe kommen können wir uns am besten mit Hilfe von Abbildung 6.12 verdeutlichen.

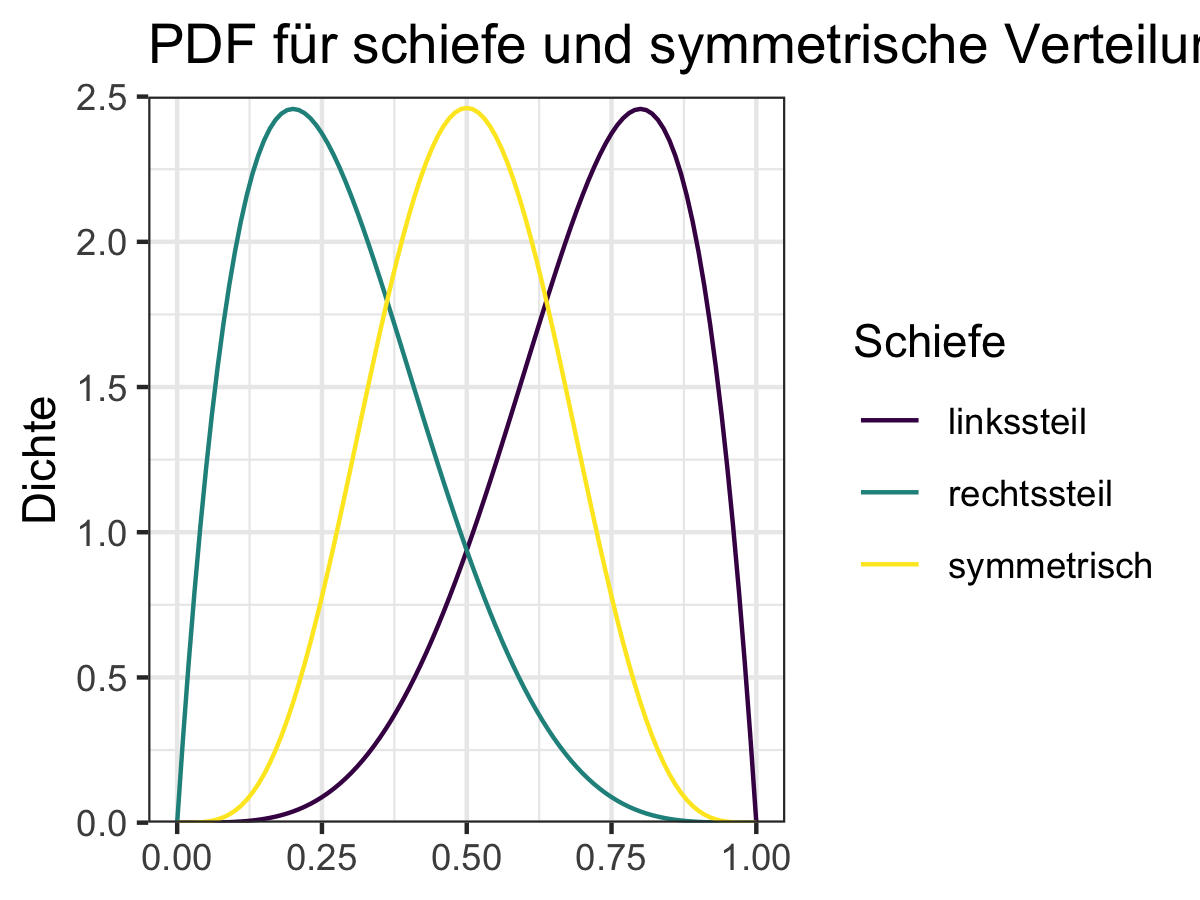
Abbildung 6.12: Beispiele für Verteilungen mit unterschiedlichen Schiefen

In R können wir die Schiefe einer Verteilung mit der Funktion skewness() aus dem Paket moments (Komsta und Novomestky 2015) berechnen:

moments::skewness(journal_daten[["Preis"]])

#> [1] 1.691223

Wir würden hier also von einer rechts-schiefen Verteilung der Preise sprechen. Das sehen wir hier auch grafisch in Abbildung 6.13.

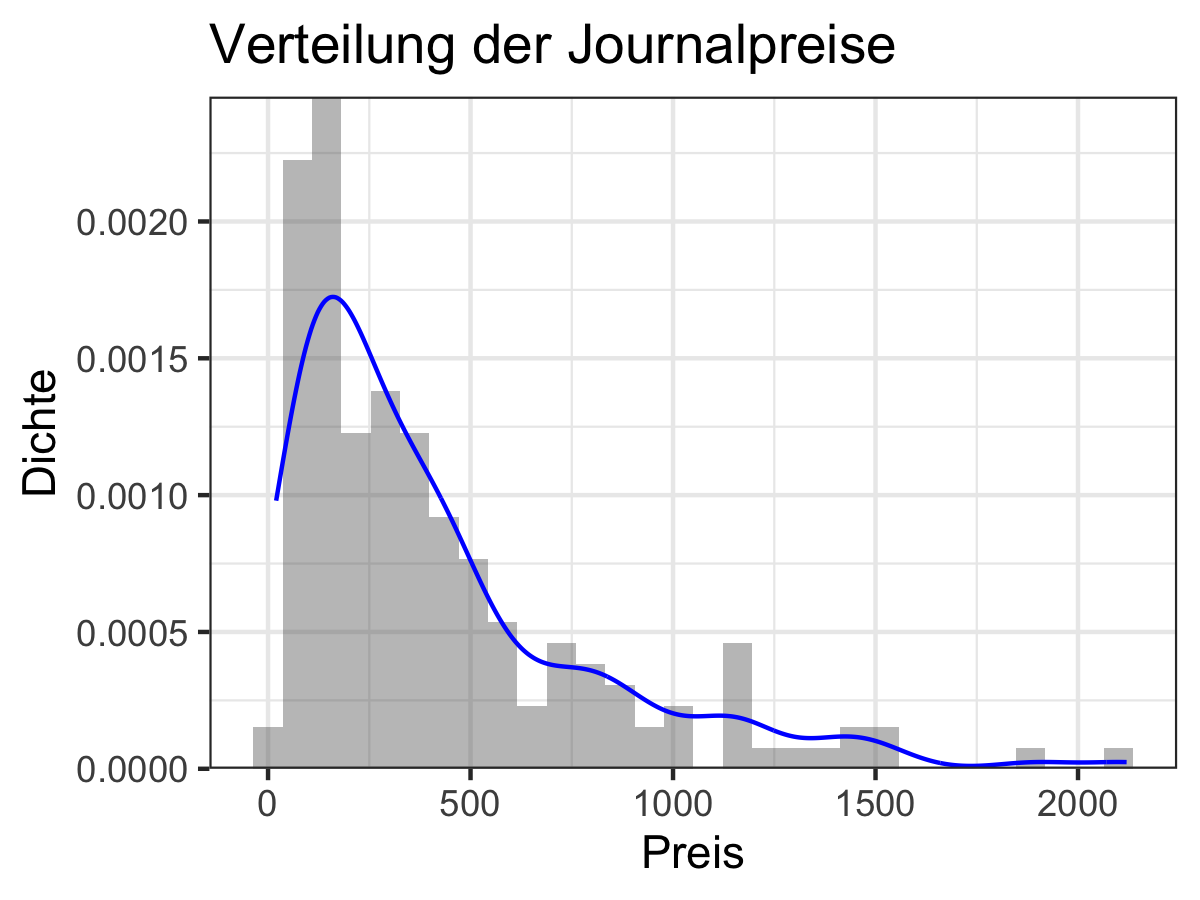
Abbildung 6.13: Rechts-schiefe Verteilung der Journalpreise

Die Steile (auch: Kurtosis) \(\omega_x\) einer Verteilung gibt ihre ‘Spitzgipfligkeit’ an. Je größer \(\omega_x\) desto ‘schmaler’ wird die Verteilung und desto weniger extreme Werte hat sie. Die Steile ist folgendermaßen definiert:

\[\omega_x = \frac{1}{n}\sum_{i=1}^n\left( \frac{x_i-\bar{x}}{s_x}\right)^4\] Wie bei der Schiefe müssen wir für die Schätzung wieder für die Reduktion der Freiheitsgrade korrigieren, sodass die praktische Schätzfunktion gegeben ist durch:

\[\hat{\omega}_x = \frac{1}{(n-1)(n-2)}\sum_{i=1}^n\left( \frac{x_i-\bar{x}}{s_x}\right)^4\]

Wir können die Kurtosis einer Verteilung mit der Funktion kurtosis() aus dem Paket moments berechnen:

moments::kurtosis(journal_daten[["Preis"]])

#> [1] 5.992058

Da der Wert der Kurtosis \(\omega_x\) an sich nicht leicht zu interpretieren ist wird er häufig mit dem einer Standardnormalverteilung verglichen. Da deren Wert per definitionem 3 beträgt wird die Exzess-Kurtosis mit \(\tilde{\omega}_x=\omega_x-3\) berechnet. Wir sprechen von einer steilgipfligen (‘leptokurtischen’) Verteilung wenn \(\tilde{\omega}_x>0\) und von einer flachgipfligen (‘platykurtischen’) Verteilung wenn \(\tilde{\omega}_x<0\). Für den Fall der Preisverteilung von Journalen haben wir es also mit einer steilgipfligen Verteilung zu tun, d.h. die Verteilung der Journalpreise ist ‘schmaler’ als eine Normalverteilung.

Zur Verdeutlichung des Konzepts bietet Abbildung 6.14 ein grafisches Beispiel.

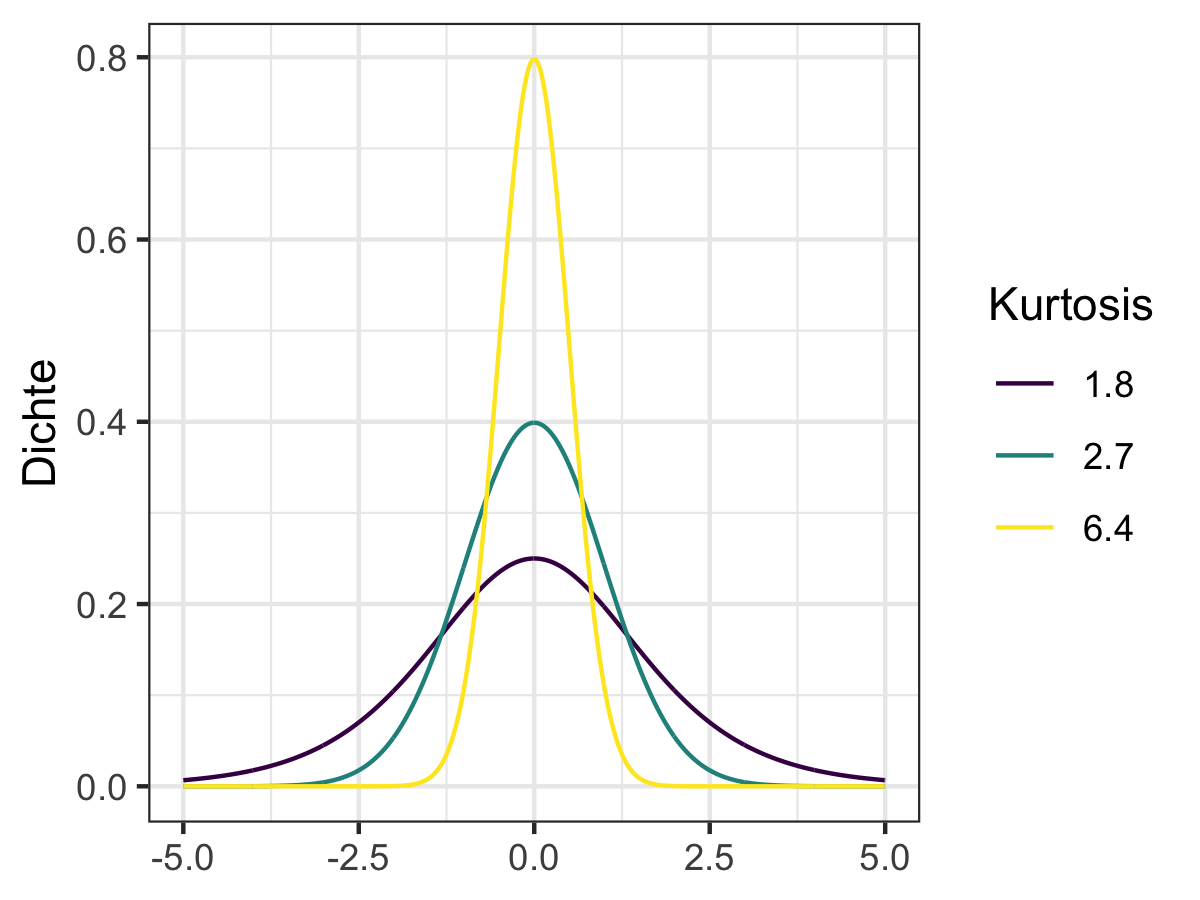
Abbildung 6.14: Beispiel von Verteilungen mit verschiedener Kurtosis

Ausreißer und Schwanz-Eigenschaften

Ausreißer können einen großen Effekt auf Ihre Ergebnisse haben. Erinnern Sie sich daran, dass der Mittelwert eines Datensatzes sehr anfällig für Ausreißer, also besonders große oder kleine Werte, ist. Gleiches gilt für viele andere Maße.

Insofern stellen sich zwei wichtige Fragen: Erstens, was genau verstehen wir unter einem Ausreißer? Zweitens, wie sollten wir mit Ausreißern umgehen?

Im Kontext eines Boxplot wurde ein Ausreißer als ein Wert der außerhalb des Intervalls \(\left( x_{0.25} - IQR\cdot 1.5, x_{0.75} + IQR\cdot 1.5 \right)\) liegt definiert. Dies führt häufig zu einer zu recht restriktiven Definition von Ausreißern, ist aber ein guter erster Schritt. Wir können die Ausreißer hier einfach identifizieren indem wir den Datensatz entsprechend filtern, z.B.:

IQR_Grenzen <- quantile(journal_daten[["Preis"]], c(0.25, 0.75))
untere_grenze <- IQR_Grenzen["25%"] - 1.5*IQR(journal_daten[["Preis"]])
obere_grenze <- IQR_Grenzen["75%"] + 1.5*IQR(journal_daten[["Preis"]])

outlier_teuer <- journal_daten %>%
  dplyr::filter(Preis > obere_grenze)

outlier_billig <- journal_daten %>%
  dplyr::filter(Preis < untere_grenze)
 

dplyr::select(outlier_teuer, Titel, Preis)

#>                                           Titel Preis
#>  1:                        Ecological Economics  1170
#>  2:                           Applied Economics  2120
#>  3:              Journal of Banking and Finance  1539
#>  4: Journal of Economic Behavior & Organization  1154
#>  5:                             Research Policy  1234
#>  6:                           Economics Letters  1492
#>  7:                    European Economic Review  1154
#>  8:                           World Development  1450
#>  9:                 Journal of Public Economics  1431
#> 10:                     Journal of Econometrics  1893
#> 11:                  Journal of Economic Theory  1400
#> 12:              Journal of Financial Economics  1339

dplyr::select(outlier_billig, Titel, Preis)

#> Empty data.table (0 rows and 2 cols): Titel,Preis

Wir sehen hier, dass es nur Ausreißer nach oben, also nur besonders teure Journale gibt. Nun können/müssen wir uns für diese Fälle überlegen wie wir mit den Ausreißern umgehen wollen.

Manche Ausreißer sind die Folge von Messfehlern oder Fehlern in der Datenaufbereitung. Idealerweise würden wir solche Ausreißer aus dem Datensatz entfernen wollen.

Andere Ausreißer sind dagegen einfach besonders interessante Datenpunkte, die auf gar keinen Fall aus dem Datensatz entfernt werden sollten. So hat Luxenburg im Vergleich zu anderen Europäischen Ländern ein wahnsinnig hohes Einkommensniveau, aber das bedeutet nicht, dass wir Luxenburg aus allen Analysen herausnehmen sollten. Im Bereich der Finanzmarktanalyse sind extreme Preisausschläge häufig gerade besonders relevant. Sie dürfen auf gar keinen Fall ausgeschlossen werden, denn häufig sind sie Ausgangspunkt von Krisen.

Häufig werden solche Ausreißer eliminiert da die Daten ohne sie leicht durch eine Normalverteilung approximiert werden können. Rechnet man mit diesen Modellen unterschätzt man aber per definitionem die Wahrscheinlichkeit für Extremwerte in der Zukunft. Daher ist die beste Vorgehensweise, sich Ausreißer explizit anzuschauen, indem wir den Datensatz nach extremen Werten (oder Werten mit einer hohen Cook’schen Distanz) filtern und dann selbst entscheiden ob diese Werte eher Resultat eines Messfehlers oder ein besonders interessanter Wert sind. Es gilt jedoch: im Zweifel sollten die Datenpunkte immer im Datensatz gelassen werden. Ein Ausreißer darf nur eliminiert werden wenn es wirklich sehr gute Gründe dafür gibt.

Im Falle der Journale ist es fraglich ob es wirklich gute Gründe gibt, diese 12 Journale als Ausreißer zu eliminieren. Im vorliegenden Fall spricht wenig dafür und wir sollten uns eher überlegen wie diese besondere Stellung der Journale erklärt werden kann, z.B. über ihre Popularität.

In diesem Kontext macht es auch Sinn die Kategorie der endlastigen oder der
heavy-tailed Verteilungen einzuführen. Darunter verstehen wir Verteilungen, die besonders viele Extremwerte aufweisen - oder technisch: deren Dichte sub-exponentiell abfällt, deren Extremevents also wahrscheinlicher sind als bei der Exponentialverteilung.

Einkommens- und Vermögensverteilungen sind in der Regel heavy-tailed: es gibt zwar sehr viele Menschen mit geringen, und nur wenige mit sehr hohen Einkommen, aber mehr Menschen mit hohen Einkommen als wir es bei einer Exponentialverteilung erwarten würden.

Eine alternative Definition von Ausreißern im Kontext der Regressionsanalyse ist die Berechnung der ‘Cook’schen Distanz’ für jeden Beobachtungswert. Die ‘Cook’sche Distanz’ wird immer im Hinblick auf ein bestimmtes Regressionsmodell berechnet und gibt den Einfluss einer jeden Variable auf das Endergebnis an. Dann kann man sich die einflussreichsten Variablen genauer anschauen und sich fragen wie mit diesen Datenpunkten umzugehen ist.

Die Grundidee der ‘Cook’schen Distanz’ ist für jede Beobachtung das Regressionsergebnis zu vergleichen mit dem hypothetischen Fall, dass diese Beobachtung ausgelassen worden wäre.

Wir können für ein bestimmtes Regressionmodell die Cook’sche Distanz mit der Funktion cooks.distance() berechnen. Zum Zwecke der Illustration regressieren wir in dem Journaldatensatz die Variable ‘Preis’ auf die Variablen ‘Seitenanzahl’ und ‘Zitationen’:

reg_objekt <- lm(Preis ~ Seitenanzahl + Zitationen, 
                 data = journal_daten)
distanzen <- cooks.distance(reg_objekt)

Ab wann eine Beobachtung als Ausreißer im Sinne von der Cook’schen Distanz gilt ist nicht klar zu definieren. Als Daumenregel hat sich die Grenze \(\frac{4}{n-k-1}\) etabliert, aber in der Praxis ergibt es immer Sinn einfach die Werte mit der größten Distanz genauer anzuschauen. Diese lassen sich aus Abbildung 6.15.

#>  [1] "Managerial and Decision Econ"   "Applied Economics"             
#>  [3] "Journal of Banking and Finance" "Economics Letters"             
#>  [5] "World Development"              "Journal of Public Economics"   
#>  [7] "Journal of Economic Literature" "Journal of Econometrics"       
#>  [9] "Journal of Economic Theory"     "Economic Journal"              
#> [11] "Journal of Financial Economics" "Journal of Finance"            
#> [13] "Econometrica"

Abbildung 6.15: Betrachtung der Ausreißer nach der Cook’schen Distanz

6.4.3 Grafische Komplemente zu klassischen Kennzahlen

Ein hilfreiches Mittel zur Beschreibung von Verteilungen ist der Boxplot. Bei dem Boxplot handelt es sich um eine grafischen Zusammenfassung einiger zentraler deskriptiver Kennzahlen, wie in Abbildung 6.16 zu sehen ist.

boxplot_plot <- ggplot2::ggplot(
  data = wb_data, 
  mapping = aes(x=region, y=Lebenserwartung)
  ) +
  ggplot2::geom_boxplot() +
  ggplot2::theme_bw() +
  ggplot2::labs(
    title = "Lebenserwartungen in den Weltregionen", 
    caption = "Quelle: Weltbank") +
  ggplot2::theme(
    axis.title.x = element_blank(), 
    axis.text.x = element_text(angle = 10, vjust = 0.65))

knitr::include_graphics(plot_file, auto_pdf = T)

Abbildung 6.16: Darstellung der Lebenserwartungen in den Weltregionen anhand eines Boxplots

Im Boxplot werden mehrere relevante Kennzahlen zusammengefasst. Eine schöne Übersicht bietet Abbildung 6.17:

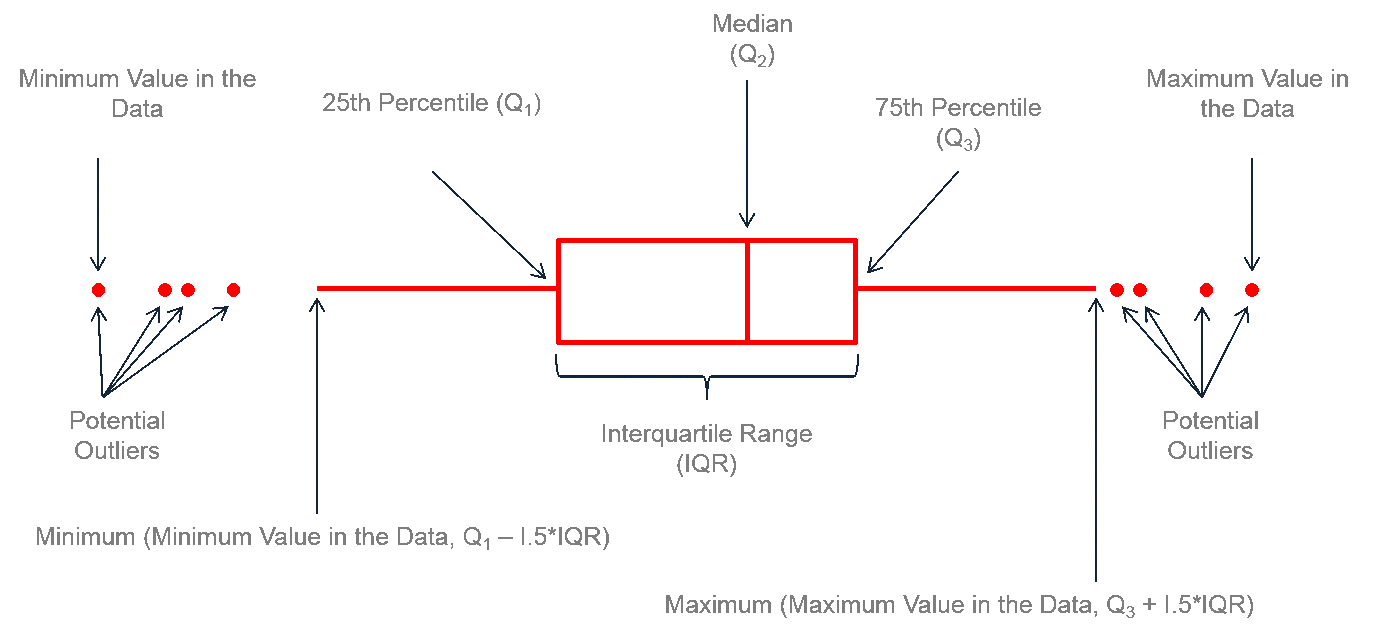
Abbildung 6.17: Boxplot Anatomie. Quelle: https://www.leansigmacorporation.com/box-plot-with-minitab/

Die Box in der Mitte des Boxplots repräsentiert die IQR der Daten, der Median ist mit einem Strich innerhalb der Box dargestellt. Die Striche an der Box repräsentieren dann das Intervall bis zum größten bzw. kleinsten Wert, der nicht weiter als \(1.5\cdot IQR\) vom Median entfernt ist. Ausreißer, hier definiert als Werte außerhalb dieses Intervalls, werden dann durch einzelne Punkte visualisiert. Selbstverständlich können Sie das Aussehen noch weiter an Ihre Präferenzen anpassen. Die Parameter dazu sind in der Hilfefunktion beschrieben. Sehr gute Anleitungen finden sich zudem hier und hier.

In diesem Post werden auch die Nachteile dieser Visualisierungsform sehr gut beschrieben. Der größte Nachteil liegt zweifellos im Verstecken der eigentlichen Verteilung ‘hinter der Box’. Es ist nicht klar, ob sich ein Großteil der Daten am oberen oder unteren Teil befindet oder ob die Daten eher gleichverteilt sind. Eine einfache Lösung für kleinere Datensätze liegt in der Ergänzung der einzelnen Beobachtungen durch boxplot_jitter, wobei sie hier die Transparenz durch alpha=0.25 anpassen sollten, und den Boxplot zur besseren Lesbarkeit über die Beobachtungen plotten sollten. Für größere Datensätzen können Sie einfach einen Violinenplot verwenden, wie in Abbildung 6.18 gezeigt.

boxplot_classic <- ggplot2::ggplot(data = wb_data, 
       mapping = aes(x=region, y=Lebenserwartung)
       ) +
  ggplot2::geom_boxplot() +
  ggplot2::theme_bw() +
  ggplot2::labs(title = "Klassisch") +
  ggplot2::theme(axis.title.x = element_blank(), 
        axis.text.x = element_text(angle = 90, hjust = 1))

boxplot_jitter <- ggplot2::ggplot(data = wb_data, 
       mapping = aes(x=region, y=Lebenserwartung)
       ) +
  ggplot2::geom_boxplot() +
  ggplot2::geom_jitter(alpha=0.25) +
  ggplot2::theme_bw() +
  ggplot2::labs(title = "Klassisch mit jitter") +
  ggplot2::theme(axis.title.x = element_blank(), 
        axis.text.x = element_text(angle = 90, hjust = 1))

violin_plot <- ggplot2::ggplot(data = wb_data, 
       mapping = aes(x=region, y=Lebenserwartung)
       ) +
  ggplot2::geom_violin() +
  ggplot2::theme_bw() +
  ggplot2::labs(title = "Violinen-Plot") +
  ggplot2::theme(axis.title.x = element_blank(), 
        axis.text.x = element_text(angle = 90, hjust = 1))

compare_plot <- ggpubr::ggarrange(
  boxplot_classic, boxplot_jitter, violin_plot, 
  ncol = 3)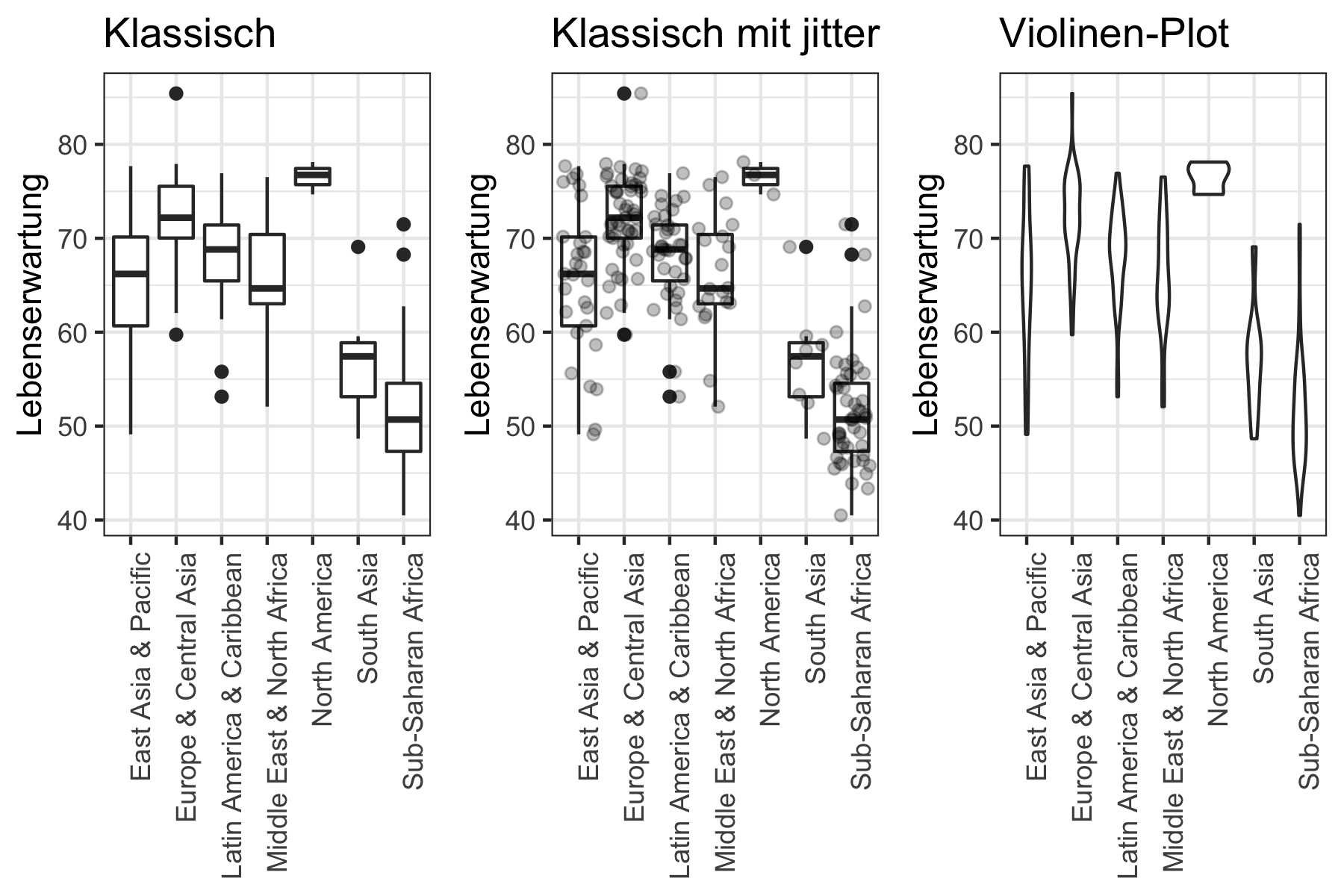

Abbildung 6.18: Vergleich von klassischen Darstellungen und dem Violinenplot

Beachten Sie, dass es immer wichtig ist, eine Verteilung nicht nur mit quantitativen Kennzahlen, sondern auch grafisch zu beschreiben und zu analysieren: andernfalls übersehen Sie leicht wichtige Strukturen in den Daten (siehe dazu auch Abschnit 8.3 in Kapitel 8).

6.4.4 Abschließende Bemerkungen

Es ist wichtig, dass wir uns mit der Verteilung unserer Daten nicht nur theoretisch, sondern auch empirisch und praktisch auseinandersetzen. Für viele Verteilungen sind z.B. bestimmte Kennzahlen nicht definiert. So hat zum Beispiel die bei Vermögens- und Einkommensverteilungen häufig zu beobachtende Pareto-Verteilungen häufig keinen wohldefinierten Mittelwert und keine wohldefinierte Varianz. Daher haben aus Stichproben geschätzte Kennzahlen, die sich dieser Konzepte bedienen, keine wirkliche Aussagekraft. Eine exzellente Beschreibung der Probleme, möglicher Alternativen und ein gutes Anwendungsbeispiel findet sich z.B. in Yang u. a. (2019).

---

44. Der Funktionsname ‘lag’ und ‘lead’ wird leider in sehr vielen Paketen verwendet, u.a. auch in data.table. Deswegen ist es gerade bei diesen Funktionen besser den expliziten Aufruf dplyr::lag() und dplyr::lead() zu verwenden.↩︎

45. Zur Transformation der y-Achse verwenden wir in ggplot2 die Funktion scale_y_continuous() und setzen das Argument trans = "log".↩︎

46. Diese Klassifizierung ist nicht erschöpfend und in einigen Fällen uneindeutig. Tatsächlich gilt Folgendes: sei \(f^n(x)\) die \(n\)-te Ableitung von \(f(x)\). Wenn \(f'(x)=0\) und die erste von Null verschiedene höhere Ableitung eine Ableitung gerader Ordnung ist haben wir einen Extrempunkt, ansonsten einen Sattelpunkt. Ansonsten gilt auch, dass bei \(f^n(x)>0\) ein Minimum und bei \(f^n(x)<0\) ein Maximum vorliegt.↩︎

47. Gerade bei komplexeren Methoden müssen Sie als Nutzer*in jedoch in der Regel nachhelfen und der Opimierungsfunktion weitere Hinweise zur Funktion angeben. Für unsere Anwendungsbeispiele ist das nicht weiter relevant, Sie sollten die Problematik jedoch im Hinterkopf behalten.↩︎

48. Es gibt auch zwei Optimierungsfunktionen in base, allerdings sind diese mittlerweile ein wenig in die Jahre gekommen. Es wird daher empfohlen, anstatt optim() und optimize() die Funktion optimx::optimr() zu verwenden, die größtenteils aber auch die gleiche Syntax verwendet. Eine Übersicht über die meisten verfügbaren Funktionen finden Sie hier.↩︎

49. Minimale Rundungsfehler sind bei solchen numerischen Verfahren normal, daher wird Ihnen in diesem Fall nicht ‘exakt’ Null als Ergebnisangezeigt.↩︎

50. Das liegt daran, dass jede \(n\times k\)-Matrix \(A\), also eine eine Matrix mit \(n\) Zeilen und \(k\) Spalten, als eine Funktion \(f(x)=Ax\) dargestellt werden kann, für die gilt: \(f: \mathbb{R}^{n}\rightarrow \mathbb{R}^k\). Diese Funktion ist immer linear. Tatsächlich gilt, dass jede Funktion \(f\) nur dann linear ist, wenn es eine Matrix \(A\) gibt, für die gilt \(f(x)=Ax\).↩︎

51. Alternativ können Sie auch die Funktion solve() aus base verwenden; hier ist das erste Argument a und der Output ist weniger informativ.↩︎

52. Wenn Sie die einzelnen Schritte zur Lösung nachverfolgen wollen, rufen Sie die Funktion mit dem Argument verbose=TRUE auf!↩︎

53. Die genaue Herleitung finden Sie im nächsten (optionalen) Abschnitt.↩︎

54. Beachte dabei, dass \(\boldsymbol{Y'X\hat{\beta}}=(\boldsymbol{Y'X\hat{\beta}})'=\boldsymbol{\hat{\beta}'X'Y}\).↩︎

55. Hier liegt übrigens auch der Grund für die OLS-Annahme, dass keine perfekte Multikollinearität besteht: denn in diesem Fall wäre eine Zeile der Matrix \(\boldsymbol{X}\) eine lineare Kombination einer anderen Zeile und \(\boldsymbol{X}\) wäre damit nicht mehr invertiertbar, also \(\boldsymbol{X}^{-1}\) würde nicht existieren und \(\boldsymbol{\hat{\beta}}\) wäre nicht mehr definiert.↩︎

56. Wir sehen unten aber auch, dass solche Kennzahlen immer mit einer grafischen Darstellung kombiniert werden sollten.↩︎

57. Ein “parametrisches Warhscheinlichkeitsmodell” meint dabei eine ZV mit bestimmten Parametern.↩︎

58. Die bekanntesten Verteilungen werden in Kapitel 7 beschrieben. Die vollständige Liste der Verteilungskürzel in R finden Sie hier.↩︎

59. Beachten Sie, dass ein solcher Test weniger gut geeignet ist, wenn Sie entscheiden wollen ob Ihre Daten normalverteilt ‘genug’ sind um bestimmte Methoden anzuwenden, die eine Normalverteilung voraussetzen. Dazu sollten Sie unbedingt auch grafische Methoden wie QQ-Plots verwenden. Für mehr Details schauen Sie mal in diesen Blogartikel.↩︎

60. Eine frei zugängliche Version des Papers findet sich hier.↩︎

61. Dieser Datensatz enthält Informationen über Preise, Seiten, Zitationen und Abonennten von 180 Journalen aus der Ökonomik im Jahr 2004.Bei den hier verwendeten Daten handelt es sich um eine Übersetzung des Datensatzes Journals aus dem Paket AER (Kleiber und Zeileis 2008).↩︎

62. Eine Abrundungsfunktion rundet eine Dezimalzahl auf die nächst-kleinere ganze Zahl ab. So ist z.B. \(\lfloor 1.9 \rfloor=1\) und \(\lfloor 1.2 \rfloor=1\).↩︎

63. Es gibt natürlich noch viele andere Möglichkeiten, siehe z.B. hier.↩︎