Chapter 9 Wiederholung: Drei Verfahren der schließenden Statistik

In diesem Kapitel werden wir drei zentrale Verfahren der schließenden Statistik wiederholen. Dabei schließen wir unmittelbar an die beiden vorangegangenen Kapitel zur Wahrscheinlichkeitstheorie und deskriptiven Statistik an. Mit Hilfe der Wahrscheinlichkeitstheorie beschreiben wir mögliche Prozesse, die unsere Daten generiert haben könnten (DGP - data generating processes). Mit Hilfe der deskriptiven Statistik beschreiben wir unsere Daten und wählen auf dieser Basis Kandidaten für den DGP und sinnvolle Schätzverfahren aus. In der schließenden Statistik geht es nun genau um diese Schätzverfahren, die es uns erlauben von unseren Daten Rückschlüsse auf die DGP zu ziehen. Eine andere Art dies auszudrücken ist: mit Hilfe der schließenden Statistik wollen wir durch Analyse unserer Stichprobe auf die Gesamtpopulation, aus der die Stichprobe gezogen wurde, schließen - und dabei möglichst die Unsicherheit, die diesem Schließprozess inhärent ist, genau quantifizieren.

Natürlich ist wie immer Vorsicht geboten: wie bei der deskriptiven Statistik suggerieren viele der quantitativen Methoden der schließenden Statistik eine Genauigkeit und Exaktheit, die in der Wirklichkeit an der Korrektheit vieler Annahmen hängt. Man darf daher nicht den Fehler machen, den ‘genauen’ Ergebnissen der schließenden Statistik unhinterfragt zu glauben. Gleichzeitig darf man sie auch nicht verteufeln, denn viele Annahmen kann man mit ein wenig formalem Geschick und theoretischen Kenntnissen auch sinnvoll hinsichtlich ihrer Angemessenheit überprüfen.

Dafür ist es wichtig, die Grundlagen der schließenden Statistik gut verstanden zu haben. In diesem Kapitel wiederholen wir diese Grundlagen grob und kombinieren die Wiederholung mit einer Einführung in die entsprechenden Befehle in R.

Wie oben bereits angekündigt gehen wir in der Regel davon aus, dass die von uns beobachteten Daten das Resultat eines gewissen Zufallsprozesses ist, den wir mit Hilfe der Wahrscheinlichkeitstheorie mathematisch beschreiben können. Da wir den DGP aber nicht direkt beobachten können, müssen wir auf Basis von empirischen Hinweisen und theoretischem Wissen entscheiden, welches Wahrscheinlichkeitsmodell wir unserer Analyse zugrunde legen. Sobald wir das getan haben, versuchen wir die Parameter, die für das von uns ausgewählte wahrscheinlichkeitstheoretische Modell relevant sind, so zu wählen, dass sie die Daten möglichst gut erklären können. Man nennt derlei Ansätze in der Statistik parametrische Verfahren, weil man mit den Daten die Parameter eines Modells bestimmen will, das man vorher selbst ausgewählt hat. Alternativ gibt es auch nicht-parametrische Verfahren: hier wird auch das Modell auf Basis der Daten bestimmt. Hier beschäftigen wir uns jedoch nur mit den parametrischen Verfahren.

In diesem Kontext sind drei Vorgehen in der statistischen Analyse besonders gängig:

Punktschätzung
Statistische Tests
Konfidenzintervalle

Wir wollen die verschiedenen Vorgehensweisen anhand eines Beispiels durchspielen: Nehnem wir an wir haben einen Datensatz und wir nehmen an, dass diese Daten von einer Binominalverteilung stammen.⁷⁶ Wir wissen, dass die Binominalverteilung durch zwei Parameter spezifiziert wird: $n$ als die Anzahl der Versuche und $p$ als die Erfolgswahrscheinlichkeit für den einzelnen Versuch. Wir sind nun daran interessiert auf Basis von unseren Daten Aussagen über den Paramter $p$ der zugrundeliegenden Binominalverteilung zu treffen. Die Annahme, dass die Daten überhaupt von einer Binominalverteilung stammen wird hier nicht in Frage gestellt. Das ist genau die Vor-Annahme, die wir bei parametrischen Verfahren treffen müssen.

Wenn wir einen konkreten Wert für $p$ herausbekommen wollen müssen wir ein Verfahren der Punktschätzung wählen.
Wenn wir wissen wollen ob ein bestimmter Wert für $p$ gegeben der Daten plausibel ist, dann sollten wir mit statistischen Tests (oder ‘Hypothesentests’) arbeiten. Wenn wir schließlich ein Intervall für $p$ spezifizieren wollen, das mit den Beobachtungen kompatibel ist, dann suchen wir nach einem Konfidenzintervall für $p$.

Im Folgenden werden die drei Verfahren in größerem Detail besprochen.

Verwendete Pakete

library(here)
library(tidyverse)
library(ggpubr)
library(latex2exp)
library(AER)
library(MASS)

9.1 Punktschätzung

Bei der Punktschätzung geht es darum auf Basis der Daten konkrete Werte für die Parameter der den Daten zugrundeliegenden Verteilung zu schätzen. In der Regel bezeichnet man den Parameter, den man schätzen möchte, mit dem Symbol $\theta$. Der Grund ist Faulheit und bessere Lesbarkeit: man kann dann nämlich die selbe Notation verwenden, egal welche zugrundeliegende Verteilung man vorher ausgewählt hat.

Im vorliegenden Fall wollen wir also einen konkreten Wert für $\theta$ auf Basis der Daten schätzen. Dabei ist ganz wichtig zu beachten, dass wir den wahren Wert von $\theta$ in der Regel nicht kennen und auch nie genau kennen werden.

Um zwischen dem wahren, für uns nicht zugänglichen Wert von $\theta$ und dem Schätzer für $\theta$ in unserer Notation unterscheiden zu können, verwenden wir das $\hat{\cdot}$-Symbol. Entsprechend bezeichnet $\hat{\theta}$ einen Schätzer für $\theta$.

Ein Schätzer ist dabei eine Funktion, die als Input unsere Daten nimmt, und als Output einen Wert ausgibt, der eine möglichst gute Schätzung für $\theta$ darstellt. Entsprechend können wir für eine Stichprobe vom Umfang $n$ schreiben:

\[\hat{\theta}: \mathbb{R}^n \rightarrow \mathbb{R}, \quad \hat{\theta}=\hat{\theta}(x_1,...,x_n)\]

Damit ist auch klar, dass es sich bei einem Schätzer um eine Zufallsvariable (ZV) handelt: Funktionen von ZV sind selbst ZV und unsere Daten $x_1,...,x_n$ interpretieren wir ja als Realisierungen von ZV $X_1,...,X_n$. Der unbekannte wahre Wert $\theta$ ist dagegen keine ZV.

Hinweis: Schätzer vs. geschätzter Wert Die Unterscheidung zwischen einem Schätzer (estimator) und einem geschätzten Wert (estimate) ist in der Statistik zentral: der Schätzer beschreibt die Prozedur einen geschätzten Wert zu bekommen. Er nimmt in der Regel die Form einer Formel oder eines Algorithmus an. Der geschätzte Wert ist für einen konkreten Anwendungsfall der Wert, den der Schätzer liefert.

Die Konstruktion von Schätzern ist keine einfache Aufgabe. In der Geschichte haben sich verschiedene Methoden, wie die Momentenmethode und die Maximum-Likelihood Methode entwickelt und alle haben ihre Vor- und Nachteile. Einige dieser Methoden werden wir in späteren Kapiteln (u.a. Kapitel 10, 11 und 12) noch genauer kennen lernen.

9.2 Hypothesentests

Wir verwenden statistische Tests um Fragen der folgenden Art zu beantworten: gegeben der Daten die wir sehen und der Annahmen, die wir treffen, ist ein bestimmter Wert für Parameter $\theta$ plausibel?

Beispiel: Das klassische Beispiel ist die Frage, ob eine Münze manipuliert wurde oder nicht. Wenn wir beim Ereignis ‘Zahl’ von Erfolg sprechen, dann können wir $n$ Münzwürfe als Binomialverteilung mit $B(n,p)$ modellieren. Bei einer nicht manipulierten Münze wäre $p=0.5$: die Wahrscheinlichkeit, dass wir das Ereignis ‘Zahl’ erleben liegt beim einzelnen Wurf bei 50%. Nennen wir das unsere Ausgangs-, oder Nullhypothese. Zur Überprüfung dieser Hypothese werfen wir die Münze nun 100 mal. Nehmen wir nun an, dass wir das Ereignis ‘Zahl’ in 60 von 100 Würfen beobachten. Bedeutet das, dass unsere Nullhypothese von $p=0.5$ plausibel ist? Um diese Frage zu beantworten fragen wir uns, wie wahrscheinlich es bei $p=0.5$ wäre, tatsächlich 60 mal Zahl zu beobachten. Diese Wahrscheinlichkeit können wir berechnen, aus Tabellen auslesen oder von R bestimmen lassen (die genaue Verwendung der Funktion binom.test() wird unten genauer besprochen):

b_test_object <- binom.test(x = 60, n = 100, p = 0.5)
b_test_object[["p.value"]]

#> [1] 0.05688793

Die Wahrscheinlichkeit liegt also bei 5.7 %. Dies ist der so genannte p-Wert. In der Regel lehnt man eine Hypothese ab, wenn $p<0.1$ oder $p<0.05$. Im vorliegenden Falle ist unsere Hypothese einer fairen Münze aber kompatibel mit der Beobachtung von 60 mal Zahl.

Wir wollen nun das Vorgehen aus dem Beispiel generalisieren und das standardmäßige Vorgehen bei einem statistischen Test zusammenfassen:⁷⁷

1. Schritt: Aufstellen eines wahrscheinlichkeitstheoretischen Modells Zunächst müssen wir eine Annahme über den Prozess treffen, welcher der Generierung unserer Daten zugrunde liegt. Im Beispiel oben haben wir eine Binomialverteilung $\mathcal{B}(n,p)$ angenommen. Diese Entscheidung muss auf Basis von theoretischen und empirischen Überlegungen getroffen werden. Für diskrete Daten ergibt es z.B. keinen Sinn eine stetige Verteilung anzunehmen und umgekehrt.

2. Schritt: Formulierung der Nullhypothese Die Hypothese, die wir mit unseren Daten testen wollen wird Nullhypothese genannt. Wir wollen also immer fragen, ob $H_0$ gegeben der Daten plausibel ist. Die Formulierung von $H_0$ wird also durch unser Erkenntnisinteresse bestimmt. In der Regel formulieren wir eine Hypothese, die wir verwerfen wollen als $H_0$.⁷⁸ Wenn wir also die Hypothese bezüglich eines Parameters $\theta$ testen wollen, dass $\beta\neq 0$, dann formulieren wir $H_0: \theta = 0$. Anders formuliert: wir möchten andere mit den Daten überzeugen, dass $H_0$ falsch ist.

Aus der Nullhypothese und unserem Erkenntnisinteresse ergibt sich die Alternativhypothese $H_1$. Sie umfasst alle interessierenden Ereignisse, die $H_0$ widersprechen. Je nachdem wie wir $H_1$ formulieren unterscheiden wir folgende Arten von Hypothesentests:

$H_0: \theta=0$ und $H_1: \theta\neq 0$: hier sprechen wir von einem zwei-seitigen Test, denn wir machen keine Aussage darüber ob die Alternative zu $H_0$ entweder in $\theta>0$ oder $\theta<0$ liegt. Gemeinsam decken $H_0$ und $H_1$ hier alle möglichen Ereignisse ab.

$H_0: \theta=0$ und $H_1: \theta> 0$: Hier sprechen wir von einem einseitigen Test nach oben. Wir fragen uns hier nur ob $\theta$ größer ist als 0. Der Fall, dass $\theta<0$, wird nicht beachtet. Natürlich können wir den einseitigen Test auch andersherum formulieren als $H_0: \theta=0$ und $H_1: \theta< 0$. Dann sprechen wir von einem einseitigen Test nach unten.

Beispiel: Wenn wir unser Münzbeispiel von oben betrachten können wir die drei verschiedenen Testarten folgendermaßen konkretisieren: beim zweiseitigen Test wäre $H_0: p=0.5$ und $H_1: p\neq 0.5$ und wir würden ganz allgemein fragen ob die Münze manipuliert ist. Beim einseitigen Test nach oben würden wir $H_0: p=0.5$ und $H_1: p>0.5$ testen und damit fragen ob die Münze zugunsten von Zahl manipuliert wurde. Wir lassen dabei die Möglichkeit, dass die Münze zugunsten von Kopf manipuliert wurde völlig außen vor. Beim einseitigen Test nach unten wäre es genau umgekehrt: $H_0: p=0.5$ und $H_1: p<0.5$.

3. Schritt: Berechnung einer Teststatistik Wir überlegen nun welche Verteilung unserer Daten wir erwarten würden wenn die Nullhypothese korrekt wäre. Wenn wir im ersten Schritt also eine Binomialverteilung mit $n=100$ angenommen haben und $H_0: p=0.5$, dann würden wir vermuten, dass unsere Daten gemäß $B(n, 0.5)$ verteilt sind. In der Praxis wird die Berechnung der Teststatistik durch eine R Funktion in einem der nächsten Schritte übernommen, aber es macht Sinn, sich das grundsätzliche Vorgehen dennoch in dieser Sequenz bewusst zu machen. Diese theoretische Verteilung können wir dann mit den tatsächlichen Daten vergleichen und fragen, wie wahrscheinlich es ist diese Daten tatsächlich so beobachten zu können wenn $H_0$ wahr wäre. Abbildung 9.1 veranschaulicht dies.

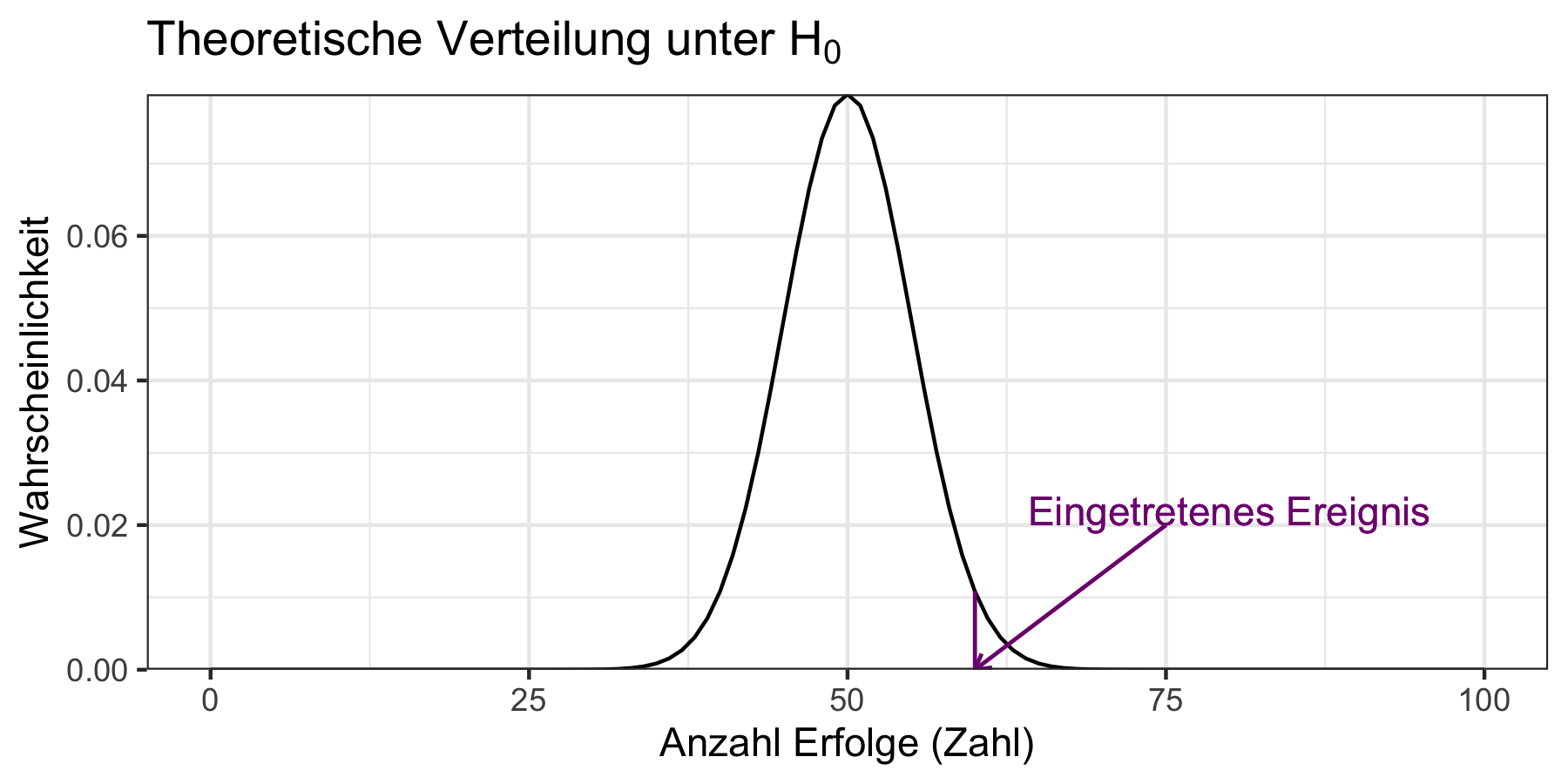
Abbildung 9.1: Vergleich unseres eingetretenen Ereignisses mit der theoretischen Verteilung unter $H_0$.

4. Schritt: Festlegung des Signifikanzniveaus: Wir müssen nun festlegen welches Risiko wir bereit sind für den Fall einzugehen, unsere Nullhypothese $H_0$ zu verwerfen, obwohl sie eigentlich richtig ist. Die maximale Wahrscheinlichkeit für dieses unglückliche Ereigns bezeichnen wir mit $\alpha$ uns sie bestimmt unser Signifikanzniveau. Typischweise nimmt man als Standardwert $\alpha=0.05$, d.h. wir konstruieren unsere Test so, dass die Wahrscheinlichkeit, dass wir $H_0$ fälschlicherweise verwerfen maximal $\alpha=0.05$ beträgt. Mit anderen Worten, wir legen hier die Wahrscheinlichkeit für einen Fehler 1. Art explizit fest. Wir sprechen von einem Fehler 1. Art wenn wir auf Basis eines Tests $H_0$ verwerfen obwohl sie eigentlich richtig ist. Von einem Fehler 2. Art sprechen wir, wenn wir $H_0$ nicht verwerfen, obwohl $H_0$ eigentlich falsch ist.

Aus dem gewählten Signifikanzniveau ergibt sich dann der Verwerfungsbereich für unsere Nullhypothese. Wenn unsere beobachteten Daten im Verwerfungsbereich liegen wollen wir $H_0$ als verworfen betrachten.⁷⁹

Es ergibt sich logisch aus dem vorher Gesagten, dass ein höheres $\alpha$ mit einem größeren Verwerfungsbereich einhergeht.

Der Verwerfungsbereich für das oben darstellte Beispiel mit $H_0: \theta=0$ und $H_1: \theta\neq 0$ ergibt sich für $\alpha=0.05$ wie in Abbildung 9.2 dargestellt.

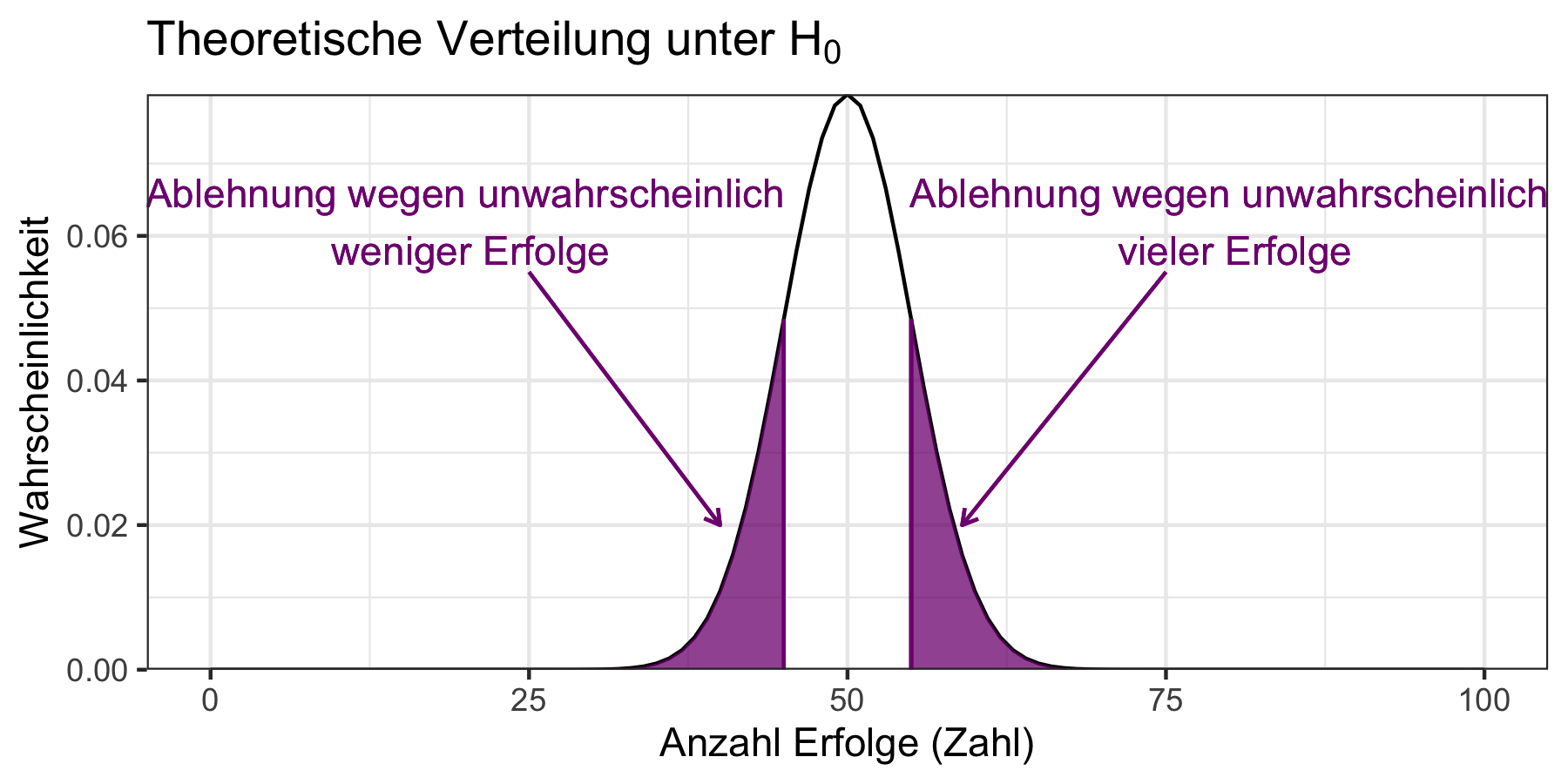
$Verwerfungsbereich der theoretischen Verteilung unter $H_0$ für $\alpha=0.05$.$

Abbildung 9.2: Verwerfungsbereich der theoretischen Verteilung unter $H_0$ für $\alpha=0.05$.

5. Schritt: Die Entscheidung Wenn sich die beobachtbaren Daten im Verwerfungsbereich befinden wollen wir $H_0$ verwerfen und die Nullhypothese entsprechend als verworfen ansehen. Falls nicht kann die Nullhypothese nicht verworfen werden - was aber nicht bedeutet, dass sie verifiziert wurde. Letzteres ist mit statistischen Tests nicht möglich.

In R werden die gerade besprochenen Tests in der Regel in einer Funktion zusammengefasst. Die Wahl der Funktion wird dabei von der im ersten Schritt angenommenen Verteilung bestimmt. Im Falle der Binomialverteilung verwenden wir die Funktion binom.test(), welche eine Liste mit relevanten Informationen über den Test erstellt. Es macht Sinn, dieser Liste einen Namen zuzuweisen und dann die relevanten Informationen explizit abzurufen:

b_test_object <- binom.test(x = 60, n = 100, p = 0.5, alternative = "two.sided")
typeof(b_test_object)

#> [1] "list"

Bevor wir uns mit dem Ergebnis befassen wollen wir uns die notwendigen Argumente von binom.test() genauer anschauen (eine gute Erläuterung liefert wie immer help(binom.test)).

Über das Argument x informieren wir R über die tatsächlich beobachtete Anzahl von Erfolgen (in unserem Fall hier 60). Das Argument n spezifiziert die Anzahl der Beobachtungen. Mit p geben wir den unter $H_0$ angenommenen Wert für die Erfolgswahrscheinlichkeit an. Mit dem Argument alternative informieren wir R schließlich darüber ob wir einen zweiseitigen (alternative = "two.sided"), einen einseitigen Test nach oben (alternative = "greater") oder einen einseitigen Test nach unten (alternative = "less") durchführen wollen.

Wenn wir einen Überblick über die Ergebnisse bekommen wollen können wir das Objekt direkt aufrufen. Die Liste wurde innerhalb der Funktion binom.test so modifiziert, dass uns die Zusammenfassung visuell ansprechend aufbereitet angezeigt wird:

b_test_object

#> 
#>  Exact binomial test
#> 
#> data:  60 and 100
#> number of successes = 60, number of trials = 100, p-value = 0.05689
#> alternative hypothesis: true probability of success is not equal to 0.5
#> 95 percent confidence interval:
#>  0.4972092 0.6967052
#> sample estimates:
#> probability of success 
#>                    0.6

Die Überschrift macht deutlich was für ein Test durchgeführt wurde und die ersten beiden Zeilen fassen noch einmal die Daten zusammen. In der zweiten Zeile findet sich zudem der p-Wert. Der p-Wert gibt die Wahrscheinlichkeit an, mit der die beobacheten Daten unter $H_0$ tatsächlich beobachtet werden können. Wir können den p-Wert aus der theoretischen Verteilung von oben auf der y-Achse ablesen, wenn wir den beobachteten Wert auf der x-Achse suchen. Dies ist in Abbildung 9.3 aufgezeigt.

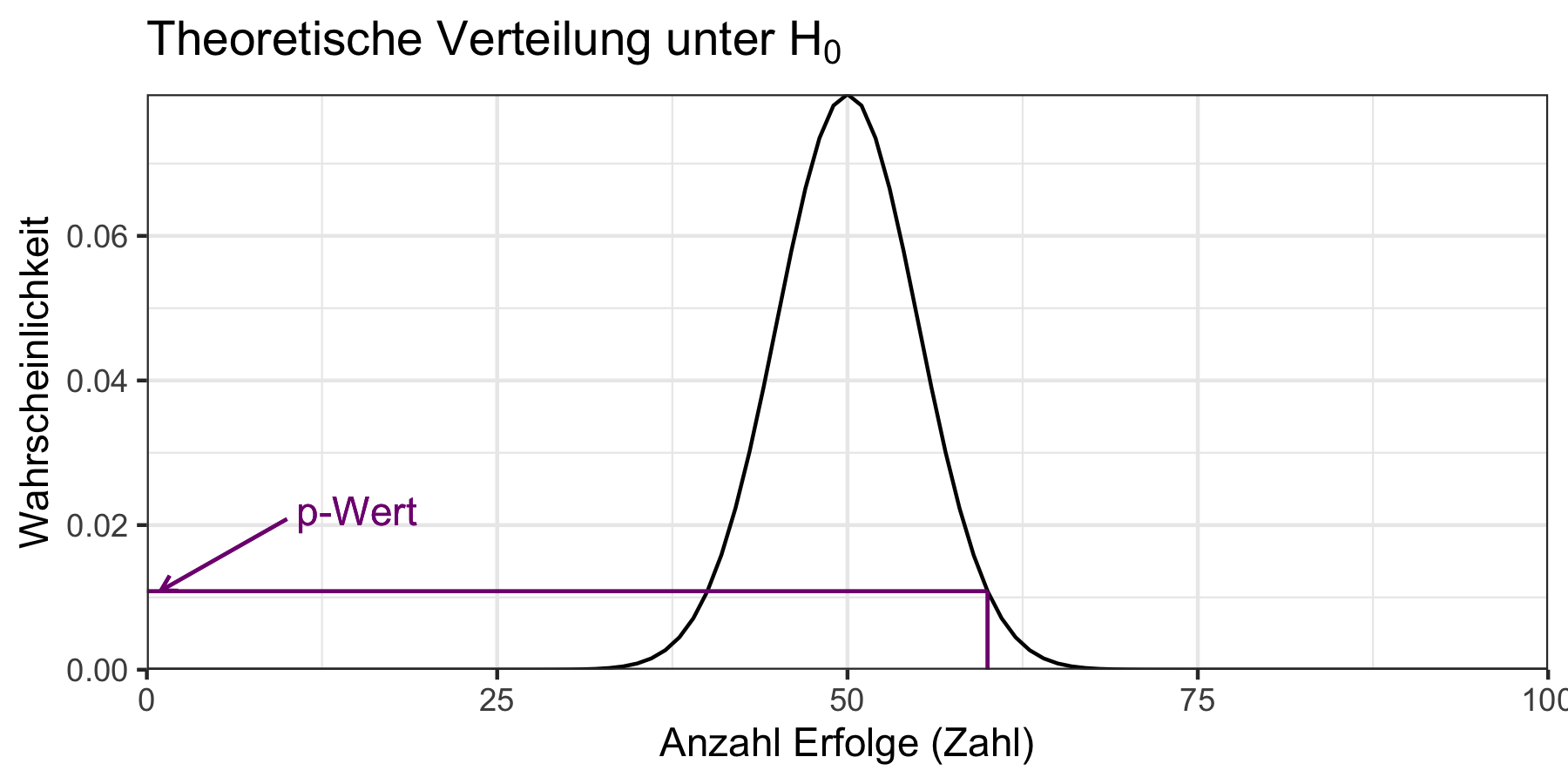
Abbildung 9.3: Ablesen des p-Werts aus der theoretischen Verteilung.

Die nächste Zeile formuliert dann die Alternativhypothese aus (und hängt entsprechend vom Argument alternative ab). Die Zeilen danach geben das 95%-Intervall an (mehr dazu im nächsten Abschnitt) und den Punktschätzer für den zu testenden Parameter (siehe vorheriger Abschnitt).

Wenn wir wissen wollen welche Informationen die so erstellte Liste sonst noch für uns bereit hält, bzw. wie wir uns diese Informationen direkt ausgeben lassen können, sollten wir uns die Struktur der Liste genauer ansehen:

str(b_test_object)

#> List of 9
#>  $ statistic  : Named num 60
#>   ..- attr(*, "names")= chr "number of successes"
#>  $ parameter  : Named num 100
#>   ..- attr(*, "names")= chr "number of trials"
#>  $ p.value    : num 0.0569
#>  $ conf.int   : num [1:2] 0.497 0.697
#>   ..- attr(*, "conf.level")= num 0.95
#>  $ estimate   : Named num 0.6
#>   ..- attr(*, "names")= chr "probability of success"
#>  $ null.value : Named num 0.5
#>   ..- attr(*, "names")= chr "probability of success"
#>  $ alternative: chr "two.sided"
#>  $ method     : chr "Exact binomial test"
#>  $ data.name  : chr "60 and 100"
#>  - attr(*, "class")= chr "htest"

Wir sehen hier, dass wir viele der Werte wie bei Listen üblich direkt anwählen können, z.B. den p-Wert:

b_test_object[["p.value"]]

#> [1] 0.05688793

Oder den Punktschätzer für $p$:

b_test_object[["estimate"]]

#> probability of success 
#>                    0.6

Wenn wir eine andere Verteilung annehmen, verwenden wir auch eine andere Testfunktion, das Prinzip ist aber sehr ähnlich. Wollen wir z.B. für einen beobachtbaren Datensatz die Hypothese testen, ob der Datensatz aus einer Normalverteilung mit dem Erwartungswert $\mu=0.5$ stammen könnte, würden wir die Funktion t.test() verwenden.

Zum Abschluss dieses Abschnitts wollen wir kurz auf die Macht von statistischen Tests (engl: Power) und auf die Wahl zwischen einseitigen und zweiseitigen Tests eingehen.

Die Macht eines Tests und Fehler 1. und 2. Art:

Wie oben bereits beschrieben sprechen wir von einem Fehler 1. Art wenn wir auf Basis eines Tests $H_0$ verwerfen obwohl sie eigentlich richtig ist. Von einem Fehler 2. Art sprechen wir, wenn wir $H_0$ nicht verwerfen, obwohl $H_0$ eigentlich falsch ist.

In der Wissenschaft hat es sich ergeben, dass man vor allem auf den Fehler 1. Art schaut. Denn man möchte auf gar keinen Fall eine Nullhypothese verwerfen, obwohl sie eigentlich richtig ist. In der Praxis würde dies bedeuten, eine Aussage zu vorschnell zu treffen. Deswegen wählt man in den empirischen Studien das Signifikanzniveau so, dass die Wahrscheinlichkeit für einen Fehler 1. Art sehr klein ist, in der Regel 5%.

Leider geht damit eine vergleichsweise hohe Wahrscheinlichkeit für einen Fehler 2. Art einher, denn die beiden Fehler sind untrennbar miteinender verbunden: reduzieren wir bei gleichbleibender Stichprobengröße die Wahrscheinlichkeit für einen Fehler 1. Art, erhöhen wir damit die Wahrscheinlichkeit für einen Fehler 2. Art und umgekehrt.

Dennoch ist auch ein Fehler 2. Art relevant. Die Wahrscheinlichkeit für einen solchen Fehler ist invers mit der Macht (engl: power) eines Tests verbunden, die definiert ist als:

\[\text{Macht}=1-\mathbb{P}(\text{Fehler 2. Art})\]

Die Abwägung zwischen den beiden Fehlern ist eine schwierige Aufgabe. Aus Konvention (und vielleicht auch der Furcht, ein Hypothese fälscherlicherweise zu verwerfen) wird in der Wissenschaft vor allem auf den Fehler erster Art geschaut. Diese Konvention ist jedoch durchaus kontrovers, siehe z.B. Ioannidis, Stanley, und Doucouliagos (2017).

Die Wahl zwischen einseitigen und zweiseitigen Tests:

Wir haben oben am Beispiel der potenziell manipulierten Münze folgendermaßen zwischen einseitigen und zweiseitigen Tests unterschieden: Beim zwei-seitigen Test testen wir $H_0: p=0.5$ gegen $H_1: p\neq 0.5$. Wir überprüfen also ob die Münze entweder zugunsten oder zulasten von Zahl manipuliert wurde.

Beim einseitigen Test testen wir nur gegen eine Alternative: $H_0: p=0.5$ bleibt gleich, allerdings ist die Alternativhypothese nun entweder $H_1: p<0.5$ oder $H_1: p>0.5$. Im ersten Fall überprüfen wir also nur ob die Münze zugunsten von Zahl manipuliert wurde, im zweiten Fall nur ob die Münze zugunsten von Kopf manipuliert wurde.

Man mag sich nun fragen wo der Vorteil von einseitigen Tests liegt, erscheint der zweiseitige Test doch allgemeiner. Letzteres ist zwar richtig, allerdings ist die Macht des zweiseitigen Tests im Vergleich zum einseitigen Tests deutlich geringer. Das bedeutet, dass wenn möglich immer der einseitige Test verwendet werden soll. Die Beurteilung ob ein einseitiger oder zweiseitiger Test angemessen ist, muss auf Basis von Vorwissen getroffen werden, und häufig spielen theoretische Überlegungen oder Kontextwissen eine wichtige Rolle.

9.3 Berechnung von Konfidenzintervallen

Konfidenzintervalle für einen Parameter geben eine Antwort auf die Frage: “Welche Werte für den interessierenden Parameter sind mit unseren Daten kompatibel?” Wie bei Hypothesentests müssen wir zur Berechnung von Konfidenzintervallen ein Signifikanzniveau $\alpha$ festlegen. Das liegt daran, dass zwischen Konfidenzintervallen und Hypothesentests eine enge Verbindung besteht: ein Konfidenzintervall $I_{\alpha}$ besteht aus allen Parameterwerten, die bei einem zweiseitigen Hypothesentest zum Signifikanzniveau $\alpha$ als Nullhypothese nicht verworfen werden können.

Wir haben oben auch schon gesehen, dass das Konfidenzintervall ganz leicht aus den typischen Test-Funktionen in R ausgelesen werden kann. Für das Beispiel der Binomialverteilung schreiben wir daher nur:

b_test_object <- binom.test(x = 60, n = 100, p = 0.5, alternative = "two.sided")
b_test_object[["conf.int"]]

#> [1] 0.4972092 0.6967052
#> attr(,"conf.level")
#> [1] 0.95

Die Interpretation dieses Intervals ist dabei die Folgende: wenn der zugrundeliegende Datengenerierungsprozess sehr häufig wiederholt werden würde, dann würde 95% der jeweils berechneten 95%-Konfidenzintervalle diesen wahren Wert enthalten. Wir können auf gar keinen Fall behaupten, dass ein bestimmtes Konfidenzintervall den wahren Parameterwert mit einer Wahrscheinlichkeit von $95$% enthält. Eine solche Aussage macht auch keinen Sinn: der wahre Wert ist - wie eingangs beschrieben - keine Zufallsvariable.⁸⁰

Wenn Sie nicht mehr wissen, was eine Binominalverteilung ist, dann lesen Sie nochmal das Kapitel 7 zur Wahrscheinlichkeitstheorie.↩︎
Wir beschränken uns hier auf so genannte parametrische Tests. Das bedeutet, dass wir zunächst ein bestimmtes Modell für den Datengenerierungsprozess annehmen. Im Beispiel war dieses Modell die Binomialverteilung. Es gibt auch Tests, die ohne eine solche Annahme auskommen. Sie werden nicht-parametrisch genannt, aber im Rahmen dieses Buches nicht behandelt. Eine eingängige Einführung findet sich z.B. in Wasserman (2006).↩︎
An manchen Stellen der sozial- und wirtschaftswissenschaftlichen Literatur wird anstelle von “verwerfen” auch das Wort “falsifizieren” benutzt um die Zurückweisung der Null-Hypothese zu umschreiben. Diese Wortwahl ist allerdings vor dem Hintergrund der Verwendung von “falsifizieren” im kritischen Rationalismus’ Karl Poppers potenziell irreführend, da hier nicht Aussagen aus einer Theorie widerlegt werden, die einen gewissen Zusammenhang behaupten. Im Gegensatz wird die Hypothese zurückgewiesen, dass der vermutete Zusammenhang eben nicht besteht - die zu Grunde gelegte Theorie wird also durch die Zurückweisung der Null-Hypothese im Normalfall nicht widerlegt sondern vielmehr bestätigt.↩︎
Zu beachten ist allerdings, dass wir nicht davon sprechen, $H_1$ ($H_0$) anzunehmen, wenn $H_0$ ($H_1$) abgelehnt wurde. Es geht hier nur um das Verwerfen von Hypothesen.↩︎
Diese Interpretation ist etwas sperrig und das hängt mit dem frequentistischen Wahrscheinlichkeitsbegriff zusammen, den wir hier verwenden. Einen philosophisch attraktiveren Weg stellt der bayessche Wahrscheinlichkeitsbegriff, auf dem die die Bayesianische Statistik aufbaut. Letztere werden wir hier allerdings nicht behandeln können↩︎